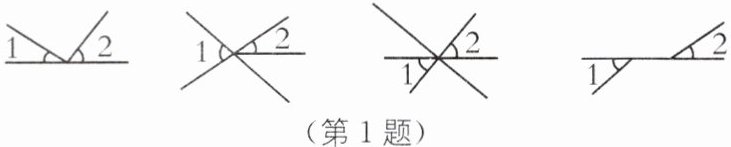
1. (教材P172练习T1·变式)下面四个图形中,∠1与∠2是对顶角的图形有(
A.1个
B.2个
C.3个
D.4个
A
).
A.1个
B.2个
C.3个
D.4个
答案:A
解析:
对顶角的定义:有一个公共顶点,并且一个角的两边分别是另一个角的两边的反向延长线,具有这种位置关系的两个角,互为对顶角。
第一个图形:∠1与∠2没有公共顶点,不是对顶角;
第二个图形:∠1与∠2的两边不互为反向延长线,不是对顶角;
第三个图形:∠1与∠2有公共顶点,且两边互为反向延长线,是对顶角;
第四个图形:∠1与∠2没有公共顶点,不是对顶角。
综上,是对顶角的图形有1个。
A
第一个图形:∠1与∠2没有公共顶点,不是对顶角;
第二个图形:∠1与∠2的两边不互为反向延长线,不是对顶角;
第三个图形:∠1与∠2有公共顶点,且两边互为反向延长线,是对顶角;
第四个图形:∠1与∠2没有公共顶点,不是对顶角。
综上,是对顶角的图形有1个。
A
2. (2025·盐城阜宁期末)如图,直线AB,CD相交于点O,OF平分∠AOC,若∠BOD= 70°,则∠DOF的度数为(

A.110°
B.145°
C.135°
D.70°
B
).
A.110°
B.145°
C.135°
D.70°
答案:B
解析:
∵直线AB,CD相交于点O,
∴∠AOC=∠BOD=70°(对顶角相等)。
∵OF平分∠AOC,
∴∠AOF=∠COF=∠AOC/2=70°/2=35°。
∵∠AOD=180°-∠BOD=180°-70°=110°,
∴∠DOF=∠AOD+∠AOF=110°+35°=145°。
B
3. (2025·南京建邺区期末)如图,直线a,b相交于点O,将量角器的中心与点O重合,发现表示60°的点在直线a上,表示140°的点在直线b上,则∠1= ______.


80°
答案:80°
解析:
140° - 60° = 80°
∠1 = 80°
∠1 = 80°
4. (教材P173练习T3·变式)如图,直线MN,PQ,ST都经过点O,若∠1= 25°,∠3= 58°,求∠2的度数.


答案:∠2=180°-∠POT-∠1=180°-∠3-∠1=180°-58°-25°=97°.
5. (2025·河南南阳南召期末)如图是一把剪刀示意图,当剪刀口∠AOB增加30°时,∠COD(

A.增加60°
B.不变
C.减少30°
D.增加30°
D
).
A.增加60°
B.不变
C.减少30°
D.增加30°
答案:D
解析:
∠AOB与∠COD是对顶角,对顶角相等。当∠AOB增加30°时,∠COD也增加30°。
D
D
6. 如图,直线AB,CD相交于点O. 已知∠BOD= 75°,OE把∠AOC分成两个角,且∠AOE= $\frac{2}{3}$∠EOC,将射线OE绕点O逆时针旋转α(0°<α<360°)到OF,当∠AOF= 120°时,α的度数是______.


答案:
90°或210° [解析]
∵∠BOD=75°,
∴∠AOC=∠BOD=75°.
∵∠AOE=$\frac{2}{3}$∠EOC,
∴∠AOE=$\frac{2}{5}$∠AOC=$\frac{2}{5}$×75°=30°.
①当OF运动到如图
(1)所示的位置时,
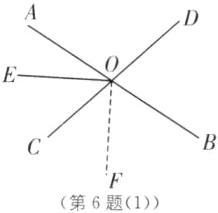
当∠AOF=120°时,α=∠EOF=∠AOF−∠AOE=120°-30°=90°;
②当OF运动到如图
(2)所示的位置时,

当∠AOF=120°时,α=360°−(∠AOF+∠AOE)=360°-120°-30°=210°.
综上所述,α的度数是90°或210°.
关键提醒 本题考查了对顶角的性质、根据比例求出角的度数以及角的和与差,能够掌握数形结合思想是解决本题的关键.
90°或210° [解析]
∵∠BOD=75°,
∴∠AOC=∠BOD=75°.
∵∠AOE=$\frac{2}{3}$∠EOC,
∴∠AOE=$\frac{2}{5}$∠AOC=$\frac{2}{5}$×75°=30°.
①当OF运动到如图
(1)所示的位置时,

当∠AOF=120°时,α=∠EOF=∠AOF−∠AOE=120°-30°=90°;
②当OF运动到如图
(2)所示的位置时,

当∠AOF=120°时,α=360°−(∠AOF+∠AOE)=360°-120°-30°=210°.
综上所述,α的度数是90°或210°.
关键提醒 本题考查了对顶角的性质、根据比例求出角的度数以及角的和与差,能够掌握数形结合思想是解决本题的关键.
7. 方程思想 如图,直线AB,CD相交于点O,已知∠AOC= 75°,∠BOE∶∠DOE= 2∶3.
(1)求∠BOE的度数.
(2)若OF平分∠AOE,∠AOC与∠AOF相等吗?为什么?

(1)求∠BOE的度数.
(2)若OF平分∠AOE,∠AOC与∠AOF相等吗?为什么?

答案:
(1)设∠BOE=2x,则∠EOD=3x,
∵∠BOD=∠AOC=75°,
∴2x+3x=75°,
解得x=15°,则2x=30°,3x=45°,
∴∠BOE=30°.
(2)相等.理由如下:
∵∠BOE=30°,
∴∠AOE=150°.
∵OF平分∠AOE,
∴∠AOF=75°,
∴∠AOC=∠AOF.
(1)设∠BOE=2x,则∠EOD=3x,
∵∠BOD=∠AOC=75°,
∴2x+3x=75°,
解得x=15°,则2x=30°,3x=45°,
∴∠BOE=30°.
(2)相等.理由如下:
∵∠BOE=30°,
∴∠AOE=150°.
∵OF平分∠AOE,
∴∠AOF=75°,
∴∠AOC=∠AOF.