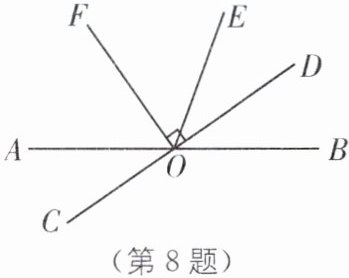
8. (2024·南京玄武区期末)如图,直线AB,CD相交于点O,∠COF= 90°,且射线OF平分∠AOE.
(1)若∠AOE= 110°,求∠DOB的度数.
(2)OD平分∠BOE吗?请说明理由.
(1)若∠AOE= 110°,求∠DOB的度数.
(2)OD平分∠BOE吗?请说明理由.

答案:
(1)
∵OF平分∠AOE,
∴∠AOF=∠FOE=$\frac{1}{2}$∠AOE=$\frac{1}{2}$×110°=55°,
∵∠COF=90°,
∴∠AOC=90°−55°=35°,
∴∠DOB=∠AOC=35°.
(2)OD平分∠BOE.理由如下:
∵OF平分∠AOE,
∴∠AOF=∠FOE.
∵∠COF=∠DOF=90°,
即∠AOC+∠AOF=90°=∠DOE+∠EOF,
∴∠AOC=∠DOE.
等角的余角相等
又∠AOC=∠BOD,
∴∠DOE=∠BOD,
即OD平分∠BOE.
(1)
∵OF平分∠AOE,
∴∠AOF=∠FOE=$\frac{1}{2}$∠AOE=$\frac{1}{2}$×110°=55°,
∵∠COF=90°,
∴∠AOC=90°−55°=35°,
∴∠DOB=∠AOC=35°.
(2)OD平分∠BOE.理由如下:
∵OF平分∠AOE,
∴∠AOF=∠FOE.
∵∠COF=∠DOF=90°,
即∠AOC+∠AOF=90°=∠DOE+∠EOF,
∴∠AOC=∠DOE.
等角的余角相等
又∠AOC=∠BOD,
∴∠DOE=∠BOD,
即OD平分∠BOE.
9. 如图,直线AB与CD相交于点E,射线EG在∠AEC内(如图(1)).
(1)若∠BEC的补角是它的余角的3倍,则∠BEC=
(2)在(1)的条件下,若∠CEG比∠AEG小25°,求∠AEG的大小;
(3)若射线EF平分∠AED,∠FEG= 100°(如图(2)),则∠AEG-∠CEG=
(1)若∠BEC的补角是它的余角的3倍,则∠BEC=
45°
;(2)在(1)的条件下,若∠CEG比∠AEG小25°,求∠AEG的大小;
∵∠BEC=45°,∴∠AEC=135°.设∠AEG=x°,则∠CEG=x°−25°.由∠AEC=135°,得x+(x−25)=135,解得x=80,∴∠AEG=80°.
(3)若射线EF平分∠AED,∠FEG= 100°(如图(2)),则∠AEG-∠CEG=
20°
.答案:
(1)45°
(2)
∵∠BEC=45°,
∴∠AEC=135°.
设∠AEG=x°,则∠CEG=x°−25°.
由∠AEC=135°,得x+(x−25)=135,
解得x=80,
∴∠AEG=80°.
(3)20° [解析]
∵射线EF平分∠AED,
∴∠AEF=∠DEF.
∵∠FEG=100°,
∴∠AEG+∠AEF=100°,
∴∠AEG=100°−∠AEF.
∵∠CEG=180°−100°−∠DEF=80°−∠DEF,
∴∠AEG−∠CEG=100°−∠AEF−(80°−∠DEF)=20°.
(1)45°
(2)
∵∠BEC=45°,
∴∠AEC=135°.
设∠AEG=x°,则∠CEG=x°−25°.
由∠AEC=135°,得x+(x−25)=135,
解得x=80,
∴∠AEG=80°.
(3)20° [解析]
∵射线EF平分∠AED,
∴∠AEF=∠DEF.
∵∠FEG=100°,
∴∠AEG+∠AEF=100°,
∴∠AEG=100°−∠AEF.
∵∠CEG=180°−100°−∠DEF=80°−∠DEF,
∴∠AEG−∠CEG=100°−∠AEF−(80°−∠DEF)=20°.
10. 中考新考法 规律探究 观察,在如图所示的各图中找对顶角(不含平角):

(1)如图(1),图中共有
(2)如图(2),图中共有
(3)如图(3),图中共有
(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成多少对对顶角?
(5)若有2000条直线相交于一点,则可形成多少对对顶角?

(1)如图(1),图中共有
2
对对顶角.(2)如图(2),图中共有
6
对对顶角.(3)如图(3),图中共有
12
对对顶角.(4)研究(1)~(3)小题中直线条数与对顶角的对数之间的关系,若有n条直线相交于一点,则可形成多少对对顶角?
2×(2−1)=2,3×(3−1)=6,4×(4−1)=12,...,∴若有n条直线相交于一点,则可形成n(n−1)对对顶角.
(5)若有2000条直线相交于一点,则可形成多少对对顶角?
2000×(2000−1)=3998000(对).故若有2000条直线相交于一点,则可形成3998000对对顶角.
答案:
(1)2
(2)6
(3)12
(4)2×(2−1)=2,3×(3−1)=6,4×(4−1)=12,...,
∴若有n条直线相交于一点,则可形成n(n−1)对对顶角.
(5)2000×(2000−1)=3998000(对).
故若有2000条直线相交于一点,则可形成3998000对对顶角.
(1)2
(2)6
(3)12
(4)2×(2−1)=2,3×(3−1)=6,4×(4−1)=12,...,
∴若有n条直线相交于一点,则可形成n(n−1)对对顶角.
(5)2000×(2000−1)=3998000(对).
故若有2000条直线相交于一点,则可形成3998000对对顶角.
11. (2024·日照中考)如图,直线AB,CD相交于点O. 若∠1= 40°,∠2= 120°,则∠COM的度数为(

A.70°
B.80°
C.90°
D.100°
B
).
A.70°
B.80°
C.90°
D.100°
答案:B [解析]
∵∠2=∠BOC=120°,∠1+∠COM=∠BOC,∠1=40°,
∴∠COM=120°−40°=80°.故选B.
∵∠2=∠BOC=120°,∠1+∠COM=∠BOC,∠1=40°,
∴∠COM=120°−40°=80°.故选B.