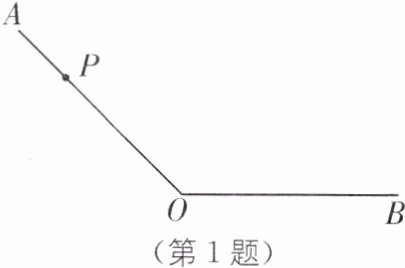
1. 作图并写出结论:如图,点P是∠AOB的边OA上一点,请过点P画出OA,OB的垂线,分别交BO的延长线于点M,N,则线段______的长表示点P到直线BO的距离;线段______的长表示点M到直线AO的距离;线段ON的长表示点O到直线______的距离;点P到直线OA的距离为______.

答案:
如图所示:

PN PM PN O
如图所示:

PN PM PN O
2. 一个角的余角比它的补角的一半小20°,求这个角的度数.
答案:设这个角的度数是x,则它的余角为90°−x,补角为180°−x.
∵这个角的余角比它的补角的一半小20°,
∴90°−x=$\frac{1}{2}$(180°−x)−20°,解得x=40°.
故这个角的度数是40°.
∵这个角的余角比它的补角的一半小20°,
∴90°−x=$\frac{1}{2}$(180°−x)−20°,解得x=40°.
故这个角的度数是40°.
3. (2024·南京玄武区期末)如图,直线AB和直线CD交于点E,EF,EG分别平分∠AEC和∠BEC.
(1)求证:EF与EG有什么位置关系,试说明原因;
(2)若∠AEF= 66°,求∠BEG的度数.

(1)求证:EF与EG有什么位置关系,试说明原因;
(2)若∠AEF= 66°,求∠BEG的度数.

答案:
(1)
∵∠AEC+∠BEC=180°,且EF,EG分别平分∠AEC和∠BEC,
∴∠FEC+∠CEG=$\frac{1}{2}$(∠AEC+∠BEC)=$\frac{1}{2}$×180°=90°,
∴EF⊥EG.
(2)由
(1)知,EF⊥EG,
∴∠FEG=90°.
∵∠AEF=66°,
∴∠BEG=180°−∠AEF−∠FEG=180°−90°−66°=24°.
(1)
∵∠AEC+∠BEC=180°,且EF,EG分别平分∠AEC和∠BEC,
∴∠FEC+∠CEG=$\frac{1}{2}$(∠AEC+∠BEC)=$\frac{1}{2}$×180°=90°,
∴EF⊥EG.
(2)由
(1)知,EF⊥EG,
∴∠FEG=90°.
∵∠AEF=66°,
∴∠BEG=180°−∠AEF−∠FEG=180°−90°−66°=24°.
4. 数形结合思想 直线AB,CD相交于点O,OF⊥CD于点O,作射线OE,且OC在∠AOE的内部.(本题所研究的角均小于180°)
(1)①当OE,OF在如图(1)所示位置时,若∠BOD= 20°,∠BOE= 130°,求∠EOF的度数;
②当OE,OF在如图(2)所示位置时,若OF平分∠BOE,试说明OC平分∠AOE.
(2)若∠AOF= 2∠COE,请直接写出∠BOE与∠AOC之间的数量关系.

(1)①当OE,OF在如图(1)所示位置时,若∠BOD= 20°,∠BOE= 130°,求∠EOF的度数;
②当OE,OF在如图(2)所示位置时,若OF平分∠BOE,试说明OC平分∠AOE.
(2)若∠AOF= 2∠COE,请直接写出∠BOE与∠AOC之间的数量关系.

答案:
(1)①
∵OF⊥CD于点O,
∴∠DOF=90°.
∵∠BOD=20°,
∴∠BOF=90°−20°=70°.
∵∠BOE=130°,
∴∠EOF=∠BOE−∠BOF=130°−70°=60°.
则∠EOF的度数为60°.
②
∵OF平分∠BOE,
∴∠EOF=∠BOF=$\frac{1}{2}$∠EOB.
∵OF⊥CD,
∴∠COF=90°,
∴∠COE+∠EOF=∠AOC+∠BOF=90°,
∴∠COE=∠AOC,即OC平分∠AOE.
(2)3∠AOC+2∠BOE=270°或∠AOC+2∠BOE=270°.理由如下:
当点E,F在直线AB的同侧时,如图
(1),
记∠COE=α,则∠AOF=2∠COE=2α,
∵OF⊥CD,
∴∠COF=90°,
∴∠EOF=90°−α,∠AOC=∠AOF−∠COF=2α−90°①,
∴∠BOE=180°−∠AOC−∠COE=180°−(2α−90°)−α=270°−3α②,
①×3+②×2,得3∠AOC+2∠BOE=270°;

当点E,F在直线AB的异侧时,如图
(2),
记∠COE=α,则∠AOF=2∠COE=2α.
∵OF⊥CD,
∴∠COF=90°,
∴∠AOC=∠COF−∠AOF=90°−2α①,
∴∠BOE=180°−∠AOC−∠COE=180°−(90°−2α)−α=90°+α②,
∴∠AOC+2∠BOE=270°.
综上可知,3∠AOC+2∠BOE=270°或∠AOC+2∠BOE =270°.
(1)①
∵OF⊥CD于点O,
∴∠DOF=90°.
∵∠BOD=20°,
∴∠BOF=90°−20°=70°.
∵∠BOE=130°,
∴∠EOF=∠BOE−∠BOF=130°−70°=60°.
则∠EOF的度数为60°.
②
∵OF平分∠BOE,
∴∠EOF=∠BOF=$\frac{1}{2}$∠EOB.
∵OF⊥CD,
∴∠COF=90°,
∴∠COE+∠EOF=∠AOC+∠BOF=90°,
∴∠COE=∠AOC,即OC平分∠AOE.
(2)3∠AOC+2∠BOE=270°或∠AOC+2∠BOE=270°.理由如下:
当点E,F在直线AB的同侧时,如图
(1),
记∠COE=α,则∠AOF=2∠COE=2α,
∵OF⊥CD,
∴∠COF=90°,
∴∠EOF=90°−α,∠AOC=∠AOF−∠COF=2α−90°①,
∴∠BOE=180°−∠AOC−∠COE=180°−(2α−90°)−α=270°−3α②,
①×3+②×2,得3∠AOC+2∠BOE=270°;

当点E,F在直线AB的异侧时,如图
(2),
记∠COE=α,则∠AOF=2∠COE=2α.
∵OF⊥CD,
∴∠COF=90°,
∴∠AOC=∠COF−∠AOF=90°−2α①,
∴∠BOE=180°−∠AOC−∠COE=180°−(90°−2α)−α=90°+α②,
∴∠AOC+2∠BOE=270°.
综上可知,3∠AOC+2∠BOE=270°或∠AOC+2∠BOE =270°.