5. 中考新考法 操作探究 已知直线AB经过点O,∠COD= 90°,OE是∠BOC的平分线.
(1)如图(1),若∠AOC= 50°,求∠DOE.
(2)如图(1),若∠AOC= α,求∠DOE.(用含α的式子表示)
(3)将图(1)中的∠COD绕顶点O顺时针旋转到图(2)的位置,其他条件不变,(2)中的结论是否还成立?试说明理由.
(4)将图(1)中的∠COD绕顶点O逆时针旋转到图(3)的位置,其他条件不变,求∠DOE.(用含α的式子表示)

(1)如图(1),若∠AOC= 50°,求∠DOE.
(2)如图(1),若∠AOC= α,求∠DOE.(用含α的式子表示)
(3)将图(1)中的∠COD绕顶点O顺时针旋转到图(2)的位置,其他条件不变,(2)中的结论是否还成立?试说明理由.
(4)将图(1)中的∠COD绕顶点O逆时针旋转到图(3)的位置,其他条件不变,求∠DOE.(用含α的式子表示)

答案:
(1)
∵∠COD=90°,
∴∠AOC+∠BOD=180°−90°=90°.
∵∠AOC=50°,
∴∠BOD=90°−50°=40°,
∴∠BOC=∠COD+∠BOD=90°+40°=130°.
∵OE平分∠BOC,
∴∠BOE=$\frac{1}{2}$∠BOC=65°,
∴∠DOE=65°−40°=25°.
(2)由
(1)可知,∠AOC+∠BOD=90°,
∵∠AOC=α,
∴∠BOD=90°−α,∠BOC=180°−α.
∵OE平分∠BOC,
∴∠BOE=$\frac{1}{2}$∠BOC=90°−$\frac{1}{2}$α,
∴∠DOE=∠BOE−∠BOD=90°−$\frac{1}{2}$α−(90°−α)=$\frac{1}{2}$α.
(3)
(2)中的结论还成立.理由如下:
∵∠AOC+∠BOC=180°,∠AOC=α,
∴∠BOC=180°−α.
∵OE平分∠BOC,
∴∠EOC=$\frac{1}{2}$∠BOC=90°−$\frac{1}{2}$α.
∵∠COD=90°,
∴∠DOE=∠COD−∠COE=90°−(90°−$\frac{1}{2}$α)=$\frac{1}{2}$α.
(4)
∵∠AOC+∠BOC=180°,∠AOC=α,
∴∠BOC=180°−α.
∵OE平分∠BOC,
∴∠EOC=$\frac{1}{2}$∠BOC=90°−$\frac{1}{2}$α.
∵∠COD=90°,
∴∠DOE=∠COD+∠COE=90°+(90°−$\frac{1}{2}$α)=180°−$\frac{1}{2}$α.
(1)
∵∠COD=90°,
∴∠AOC+∠BOD=180°−90°=90°.
∵∠AOC=50°,
∴∠BOD=90°−50°=40°,
∴∠BOC=∠COD+∠BOD=90°+40°=130°.
∵OE平分∠BOC,
∴∠BOE=$\frac{1}{2}$∠BOC=65°,
∴∠DOE=65°−40°=25°.
(2)由
(1)可知,∠AOC+∠BOD=90°,
∵∠AOC=α,
∴∠BOD=90°−α,∠BOC=180°−α.
∵OE平分∠BOC,
∴∠BOE=$\frac{1}{2}$∠BOC=90°−$\frac{1}{2}$α,
∴∠DOE=∠BOE−∠BOD=90°−$\frac{1}{2}$α−(90°−α)=$\frac{1}{2}$α.
(3)
(2)中的结论还成立.理由如下:
∵∠AOC+∠BOC=180°,∠AOC=α,
∴∠BOC=180°−α.
∵OE平分∠BOC,
∴∠EOC=$\frac{1}{2}$∠BOC=90°−$\frac{1}{2}$α.
∵∠COD=90°,
∴∠DOE=∠COD−∠COE=90°−(90°−$\frac{1}{2}$α)=$\frac{1}{2}$α.
(4)
∵∠AOC+∠BOC=180°,∠AOC=α,
∴∠BOC=180°−α.
∵OE平分∠BOC,
∴∠EOC=$\frac{1}{2}$∠BOC=90°−$\frac{1}{2}$α.
∵∠COD=90°,
∴∠DOE=∠COD+∠COE=90°+(90°−$\frac{1}{2}$α)=180°−$\frac{1}{2}$α.
6. 分类讨论思想 中考新考法 满足结论的条件开放 (2024·广东佛山南海区期末)[综合探究]如图,在直角△ABC中,∠ACB= 90°,点A在直线MN上,点D,E在直线MN上运动(点D不与点A重合),且始终满足CE平分∠BCD.
(1)当点D在点A左侧时,请直接写出∠CAD与∠CAE之间的数量关系;
(2)若∠CAE= 60°,在点D,E运动过程中,当△CDE是直角三角形时,求∠DCE的度数;
(3)请你在以点C为顶点的角中任选一个(∠BCD,∠ACD,∠ACB除外),在点D,E运动的过程中,探究所选角与∠ACD的数量关系,并写出具体过程.
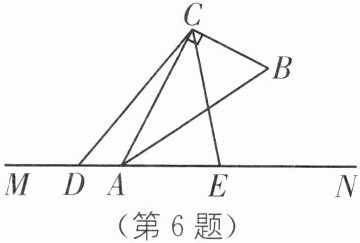
(1)当点D在点A左侧时,请直接写出∠CAD与∠CAE之间的数量关系;
(2)若∠CAE= 60°,在点D,E运动过程中,当△CDE是直角三角形时,求∠DCE的度数;
(3)请你在以点C为顶点的角中任选一个(∠BCD,∠ACD,∠ACB除外),在点D,E运动的过程中,探究所选角与∠ACD的数量关系,并写出具体过程.

答案:
(1)
∵点D,E在直线MN上运动,CE平分∠BCD,∠ACB=90°,
∴点E在点A的右侧
∵点D在点A左侧,
∴∠CAD+∠CAE=180°.
(2)
∵点D,E在直线MN上运动,CE平分∠BCD,∠ACB=90°,
∴点E在点A的右侧
∵△CDE是直角三角形,
∴∠CDE=90°或∠CED=90°,
①若∠CDE=90°,如图
(1),
则∠CAD=∠CAE=60°,∠CDA=∠CDE=90°,
∴∠ACD=180°−∠CDA−∠CAD=30°.
∵∠ACB=90°,
∴∠DCB=∠ACB−∠ACD=60°.
∵CE平分∠BCD,
∴∠DCE=∠ECB=$\frac{1}{2}$∠BCD=30°;

②若∠CED=90°,如图
(2).

∵∠CAE=60°,
∴∠ACE=180°−∠CEA−∠CAE=30°.
∵∠ACB=90°,
∴∠BCE=∠ACB−∠ACE=60°.
∵CE平分∠BCD,
∴∠DCE=∠ECB=60°.
综上所述,∠DCE=30°或∠DCE=60°.
(3)探究∠ACE与∠ACD的数量关系
∵点D,E在直线MN上运动,CE平分∠BCD,∠ACB=90°,
∴点E在点A的右侧
①点D在点A左侧时,如图
(3).

∵CE平分∠BCD,
∴∠ACD+∠ACE=∠BCE.
∵∠BCE=∠ACB−∠ACE=90°−∠ACE,
∴∠ACD+∠ACE=90°−∠ACE,
即∠ACD+2∠ACE=90°;
②点D在点A右侧时,如图
(4).
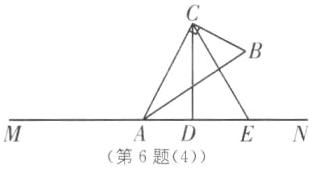
∵CE平分∠BCD,
∴∠DCE=∠ECB=$\frac{1}{2}$∠BCD.
∵∠ACE+∠ECB=∠ACB=90°,
∴∠ACD+∠BCD=∠ACD+2∠BCE=∠ACB=90°.则∠ACD+2(90°−∠ACE)=90°,
即2∠ACE−∠ACD=90°.
综上所述,∠ACE与∠ACD的数量关系为∠ACD+2∠ACE=90°或2∠ACE−∠ACD=90°.
(1)
∵点D,E在直线MN上运动,CE平分∠BCD,∠ACB=90°,
∴点E在点A的右侧
∵点D在点A左侧,
∴∠CAD+∠CAE=180°.
(2)
∵点D,E在直线MN上运动,CE平分∠BCD,∠ACB=90°,
∴点E在点A的右侧
∵△CDE是直角三角形,
∴∠CDE=90°或∠CED=90°,
①若∠CDE=90°,如图
(1),
则∠CAD=∠CAE=60°,∠CDA=∠CDE=90°,
∴∠ACD=180°−∠CDA−∠CAD=30°.
∵∠ACB=90°,
∴∠DCB=∠ACB−∠ACD=60°.
∵CE平分∠BCD,
∴∠DCE=∠ECB=$\frac{1}{2}$∠BCD=30°;

②若∠CED=90°,如图
(2).

∵∠CAE=60°,
∴∠ACE=180°−∠CEA−∠CAE=30°.
∵∠ACB=90°,
∴∠BCE=∠ACB−∠ACE=60°.
∵CE平分∠BCD,
∴∠DCE=∠ECB=60°.
综上所述,∠DCE=30°或∠DCE=60°.
(3)探究∠ACE与∠ACD的数量关系
∵点D,E在直线MN上运动,CE平分∠BCD,∠ACB=90°,
∴点E在点A的右侧
①点D在点A左侧时,如图
(3).

∵CE平分∠BCD,
∴∠ACD+∠ACE=∠BCE.
∵∠BCE=∠ACB−∠ACE=90°−∠ACE,
∴∠ACD+∠ACE=90°−∠ACE,
即∠ACD+2∠ACE=90°;
②点D在点A右侧时,如图
(4).

∵CE平分∠BCD,
∴∠DCE=∠ECB=$\frac{1}{2}$∠BCD.
∵∠ACE+∠ECB=∠ACB=90°,
∴∠ACD+∠BCD=∠ACD+2∠BCE=∠ACB=90°.则∠ACD+2(90°−∠ACE)=90°,
即2∠ACE−∠ACD=90°.
综上所述,∠ACE与∠ACD的数量关系为∠ACD+2∠ACE=90°或2∠ACE−∠ACD=90°.