9. 铅笔型 (2025·黑龙江哈尔滨香坊区期末)共享单车为市民的绿色出行提供了方便.图(1)是某品牌共享单车的实物平面图,图(2)是其部分结构示意图,其中AB// ED,$\angle ABC= 115^\circ,$$\angle EDC= 135^\circ,则\angle BCD$的度数为______°.
答案：
110 [解析]如图,过点C作CM//AB.
∵AB//ED,
∴AB//CM//ED,
∴∠ABC+∠BCM=180°,∠EDC+∠DCM=180°. 两直线平行，同旁内角互补
∵∠ABC=115°,∠EDC=135°,
∴∠BCM=65°,∠DCM=45°,
∴∠BCD=∠BCM+∠DCM=110°.
110 [解析]如图,过点C作CM//AB.
∵AB//ED,
∴AB//CM//ED,
∴∠ABC+∠BCM=180°,∠EDC+∠DCM=180°. 两直线平行，同旁内角互补
∵∠ABC=115°,∠EDC=135°,
∴∠BCM=65°,∠DCM=45°,
∴∠BCD=∠BCM+∠DCM=110°.
10. 教材P190练习T1·变式 (2024·无锡经开区期中)如图,AB// CD,点E是CD上一点,$\angle AEF= 62^\circ,$EF平分$\angle AED$交AB于点F,求$\angle AFE$的度数.
答案：
∵EF平分∠AED,
∴∠AEF=∠DEF=62°.
∵AB//CD,
∴∠AFE=∠DEF=62°.
∵EF平分∠AED,
∴∠AEF=∠DEF=62°.
∵AB//CD,
∴∠AFE=∠DEF=62°.
11.(2025·河南洛阳期末改编)如果一个角的两边与另一个角的两边相互平行,那么这两个角的大小有什么关系？
(1)小明同学首先想到如图所示的图形,他发现这两个角应该相等,你知道其中的原因是什么吗？请写出来.
(2)你是否还能发现其他图形？请画出来,并写出你所得的结论和原因.
(1)小明同学首先想到如图所示的图形,他发现这两个角应该相等,你知道其中的原因是什么吗？请写出来.
(2)你是否还能发现其他图形？请画出来,并写出你所得的结论和原因.
答案：
11.
(1)
∵AB//DE,
∴∠B=∠BGE.
∵BC//EF,
∴∠BGE=∠E,
∴∠B=∠E.
(2)我还能发现其他图形,如图
结论:如果一个角的两边与另一个角的两边相互平行，那么这两个角互补.理由:
∵AB//DE,
∴∠B=∠BGE.
∵BC//EF,
∴∠BGE+∠E=180°,
∴∠B+∠E=180°.
11.
(1)
∵AB//DE,
∴∠B=∠BGE.
∵BC//EF,
∴∠BGE=∠E,
∴∠B=∠E.
(2)我还能发现其他图形,如图
结论:如果一个角的两边与另一个角的两边相互平行，那么这两个角互补.理由:∵AB//DE,
∴∠B=∠BGE.
∵BC//EF,
∴∠BGE+∠E=180°,
∴∠B+∠E=180°.
12. 三线八角模型 中考新考法 新定义问题 (2024·盐城盐都区期中)定义：若$\angle \alpha,$$\angle \beta$是同旁内角,并且$\angle \alpha,$$\angle \beta满足\angle \beta=\angle \alpha+20^\circ,则称\angle \beta是\angle \alpha$的内联角.
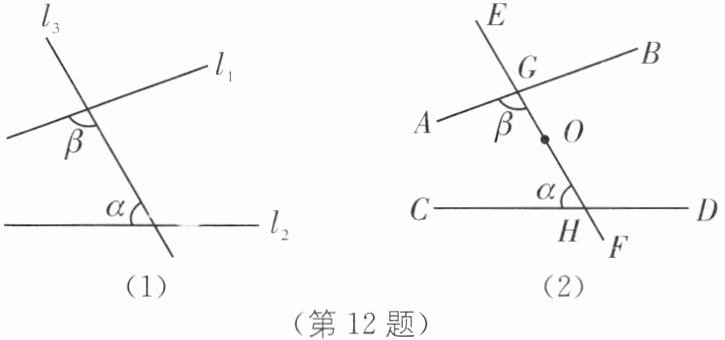
(1)如图(1),已知$\angle \beta是\angle \alpha$的内联角.
①当$\angle \alpha=60^\circ$时,$\angle \beta=______°；$
②当直线$l_1// l_2$时,求$\angle \beta$的度数.
(2)如图(2),已知$\angle \beta是\angle \alpha$的内联角,点O是线段GH上一定点$.①\angle DHG是\angle BGH$的内联角吗？请说明理由.
②过点O的直线分别交直线CD,AB于点P,Q,若$\angle \alpha=60^\circ且\angle EOP$是原图(2)中某个角的内联角.请直接写出$\angle EOP$是哪个角的内联角,以及此时$\angle EOP$的度数.
(1)如图(1),已知$\angle \beta是\angle \alpha$的内联角.
①当$\angle \alpha=60^\circ$时,$\angle \beta=______°；$
②当直线$l_1// l_2$时,求$\angle \beta$的度数.
(2)如图(2),已知$\angle \beta是\angle \alpha$的内联角,点O是线段GH上一定点$.①\angle DHG是\angle BGH$的内联角吗？请说明理由.
②过点O的直线分别交直线CD,AB于点P,Q,若$\angle \alpha=60^\circ且\angle EOP$是原图(2)中某个角的内联角.请直接写出$\angle EOP$是哪个角的内联角,以及此时$\angle EOP$的度数.
答案：
12.
(1)①80 [解析]∠β=∠α+20°=80°.②
∵$l_1$//$l_2$，∠α，∠β 是同旁内角，
∴∠α+∠β=180°.又∠β=∠α+20°，
∴∠β=100°.
(2)①是,理由如下:
∵∠β=∠α+20°,∠DHG=180°−∠α,∠BGH=180°−∠β,
∴∠DHG−∠BGH=∠β−∠α=20°,
∴∠DHG=∠BGH+20°.又∠DHG和∠BGH为同旁内角,
∴∠DHG是∠BGH的内联角.②点P在点H左侧,如图
(1)所示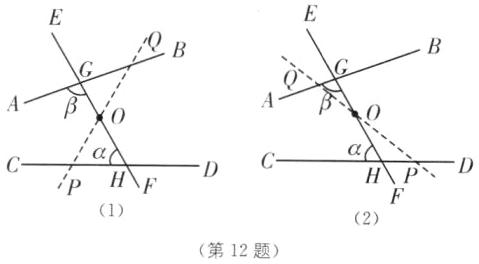
此时，∠EOP是∠β的内联角，
∴∠EOP=∠β+20°=∠α+20°+20°=100°;点P在点H右侧,如图
(2)所示.此时，∠EOP是∠BGO的内联角，
∴∠EOP=∠BGO+20°=180°−∠β+20°=180°−(∠α+20°)+20°=120°.综上所述，∠EOP是∠β的内联角时，∠EOP=100°，∠EOP是∠BGO的内联角时，∠EOP=120°.
12.
(1)①80 [解析]∠β=∠α+20°=80°.②
∵$l_1$//$l_2$，∠α，∠β 是同旁内角，
∴∠α+∠β=180°.又∠β=∠α+20°，
∴∠β=100°.
(2)①是,理由如下:
∵∠β=∠α+20°,∠DHG=180°−∠α,∠BGH=180°−∠β,
∴∠DHG−∠BGH=∠β−∠α=20°,
∴∠DHG=∠BGH+20°.又∠DHG和∠BGH为同旁内角,
∴∠DHG是∠BGH的内联角.②点P在点H左侧,如图
(1)所示
此时，∠EOP是∠β的内联角，∴∠EOP=∠β+20°=∠α+20°+20°=100°;点P在点H右侧,如图
(2)所示.此时，∠EOP是∠BGO的内联角，
∴∠EOP=∠BGO+20°=180°−∠β+20°=180°−(∠α+20°)+20°=120°.综上所述，∠EOP是∠β的内联角时，∠EOP=100°，∠EOP是∠BGO的内联角时，∠EOP=120°.