1. (2025·连云港海州区期末)下列说法中,错误的是(
A.三角形是边数最少的多边形
B.等边三角形和长方形都是正多边形
C.n边形有n条边、n个顶点、n个内角、2n个外角
D.六边形从一个顶点出发可以画3条对角线,所有的对角线共有9条
B
).A.三角形是边数最少的多边形
B.等边三角形和长方形都是正多边形
C.n边形有n条边、n个顶点、n个内角、2n个外角
D.六边形从一个顶点出发可以画3条对角线,所有的对角线共有9条
答案:B
2. (2025·扬州期末)从八边形的一个顶点出发最多可以画
5
条对角线.答案:5
解析:
从n边形的一个顶点出发可以引(n-3)条对角线。
对于八边形,n=8,所以对角线的条数为8-3=5。
5
对于八边形,n=8,所以对角线的条数为8-3=5。
5
3. a个六边形,b个五边形共有
6a+5b
条边.答案:6a+5b
4. 如图,将四边形ABCD沿虚线裁去一个角得到五边形ABCFE,则该五边形的周长
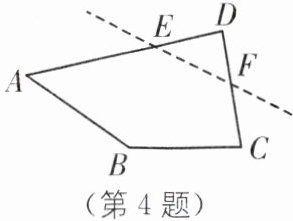
小于
原四边形的周长.(填“大于”“小于”或“等于”).
答案:小于
5. 中考新考法 归纳一般结论 如图,三角形的对角线有0条,四边形的对角线有2条,五边形的对角线有5条,六边形的对角线有9条.
(1)通过分析,请你说说十边形的对角线有多少条,你能总结出n边形的对角线有多少条吗?
(2)应用:10个人聚会,围坐在一个圆桌旁,每不相邻的人都握一次手,共握多少次手?

(1)通过分析,请你说说十边形的对角线有多少条,你能总结出n边形的对角线有多少条吗?
(2)应用:10个人聚会,围坐在一个圆桌旁,每不相邻的人都握一次手,共握多少次手?

答案:
(1)十边形的对角线有$\frac {10×(10-3)}{2}=5×7=35$(条),n边形的对角线有$\frac {n(n-3)}{2}$条.
(2)$\frac {10×(10-3)}{2}=35$(次).
故共握 35 次手.
(1)十边形的对角线有$\frac {10×(10-3)}{2}=5×7=35$(条),n边形的对角线有$\frac {n(n-3)}{2}$条.
(2)$\frac {10×(10-3)}{2}=35$(次).
故共握 35 次手.
6. 数学文化 皮克定理 各顶点都在方格纸的格点(横竖格子线的交错点)上的多边形称为格点多边形,它的面积S可用公式$S= a+\frac{1}{2}b - 1$(a是多边形内的格点数,b是多边形边界上的格点数)计算,这个公式称为“皮克(Pick)定理”.如图给出了一个格点五边形,则该五边形的面积S=
6
.答案:6 [解析]
∵a表示多边形内部的格点,b表示多边形边界上的格点,S表示多边形的面积,观察图形,可得a=4,b=6,
∴该五边形的面积S=4+1/2×6-1=6.
∵a表示多边形内部的格点,b表示多边形边界上的格点,S表示多边形的面积,观察图形,可得a=4,b=6,
∴该五边形的面积S=4+1/2×6-1=6.
7. 教材P194活动2·变式 过某个多边形一个顶点的所有对角线,将这个多边形分成6个三角形,则这个多边形的边数是
8
.答案:8 [解析]这个多边形的边数是6+2=8.
8. 已知从十边形的一个顶点出发,可以引m条对角线,这些对角线可以把这个十边形分成n个三角形,则m+n=
15
.答案:15 [解析]
∵从n边形的一个顶点出发,可以引(n-3)条对角线,把n边形分成(n-2)个三角形,
∴当n=10时,从一个顶点出发可以引7条对角线,把十边形分成8个三角形,
∴m=7,n=8,
∴m+n=15.
∵从n边形的一个顶点出发,可以引(n-3)条对角线,把n边形分成(n-2)个三角形,
∴当n=10时,从一个顶点出发可以引7条对角线,把十边形分成8个三角形,
∴m=7,n=8,
∴m+n=15.
9. 如图所示,将多边形分割成三角形.图(1)中可分割出2个三角形;图(2)中可分割出3个三角形;图(3)中可分割出4个三角形;由此你能猜测出n边形可以分割出
n-1
个三角形.答案:(n-1)[解析]由题图知,三角形分割出了2个三角形,四边形分割出了3个三角形,
∴以此类推,n边形可以分割出(n-1)个三角形.
∴以此类推,n边形可以分割出(n-1)个三角形.
10. 如图,将图(1)中的正六边形进行分割得到图(2),再将图(2)中最小的某一个正六边形按同样的方式进行分割得到图(3),再将图(3)中最小的某一个正六边形按同样的方式进行分割,…,则图(2025)中的正六边形共有
6073
个.答案:6073 [解析]第二个图形有1+3=4(个)正六边形;第三个图形有1+3+3=7(个)正六边形;…;第n个图形中,有1+3(n-1)=(3n-2)个正六边形.第2025个图形中,共有2025×3-2=6073(个)正六边形.
解析:
图
(1)有1个正六边形;
图
(2)有$1 + 3 = 4$个正六边形;
图
(3)有$1 + 3 + 3 = 7$个正六边形;
……
第$n$个图形中,正六边形的个数为$1 + 3(n - 1) = 3n - 2$。
当$n = 2025$时,$3×2025 - 2 = 6073$。
6073
(1)有1个正六边形;
图
(2)有$1 + 3 = 4$个正六边形;
图
(3)有$1 + 3 + 3 = 7$个正六边形;
……
第$n$个图形中,正六边形的个数为$1 + 3(n - 1) = 3n - 2$。
当$n = 2025$时,$3×2025 - 2 = 6073$。
6073