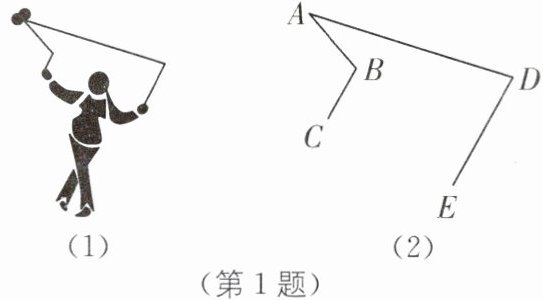
1.(2025·河南郑州中牟期末)为增强学生体质,感受中国传统文化,某初中将国家级非物质文化遗产“抖空竹”引入阳光特色大课间.如图(1)是某同学“抖空竹”时的一个瞬间,小玲把它抽象成图(2)的数学问题:已知BC//DE,∠ADE= 80°,∠ABC= 110°,则∠A的度数是( ).
A.40°
B.30°
C.20°
D.10°

A.40°
B.30°
C.20°
D.10°
答案:
B [解析]过点A作AF//BC,如图.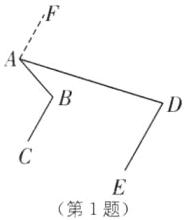
∵BC//DE,
∴AF//DE,
∴∠FAD=∠ADE=80°,∠FAB=∠ABC=110°,
∴∠BAD=∠FAB−∠FAD=30°.故选B.
B [解析]过点A作AF//BC,如图.

∵BC//DE,
∴AF//DE,
∴∠FAD=∠ADE=80°,∠FAB=∠ABC=110°,
∴∠BAD=∠FAB−∠FAD=30°.故选B.
2.(2025·内蒙古包头青山区期末)如图,若AB//CD,则α,β,γ之间的关系为( ).

A.α+β+γ= 360°
B.α-β+γ= 180°
C.α+β-γ= 180°
D.α+β+γ= 180°

A.α+β+γ= 360°
B.α-β+γ= 180°
C.α+β-γ= 180°
D.α+β+γ= 180°
答案:
C [解析]如图,作EF//AB.
∵AB//CD,AB//EF,
∴CD//EF,
∴∠BAE+∠FEA=180°,∠C=∠FEC=γ,
∴α+(β−γ)=180°.故选C.
C [解析]如图,作EF//AB.

∵AB//CD,AB//EF,
∴CD//EF,
∴∠BAE+∠FEA=180°,∠C=∠FEC=γ,
∴α+(β−γ)=180°.故选C.
3.(2025·辽宁沈阳于洪区期末)生活中常见的探照灯、汽车大灯等灯具都与抛物线有关.如图,从光源P点照射到抛物线上的光线PA,PB等反射以后沿着与EF平行的方向射出,若∠CAP= 45°,∠APB= 100°,则∠DBP的度数为(

A.45°
B.50°
C.55°
D.无法确定
C
). 
A.45°
B.50°
C.55°
D.无法确定
答案:C [解析]
∵AC//EF,∠CAP=45°,
∴∠APE=∠CAP=45°.
∵∠APB=100°,
∴∠BPE=55°.
∵BD//EF,
∴∠DBP=∠BPE=55°.故选C.
∵AC//EF,∠CAP=45°,
∴∠APE=∠CAP=45°.
∵∠APB=100°,
∴∠BPE=55°.
∵BD//EF,
∴∠DBP=∠BPE=55°.故选C.
4.(2025·河南郑州航空港区期末)如图,是路政工程车的工作示意图,工作篮底部AB与支撑平台CD平行.若∠1= 35°,∠3= 165°,则∠2的度数为______.


答案:
50° [解析]工作篮底部AB与支撑平台CD平行,如图,过点E作EF//AB,
∴AB//EF//CD,
∴∠3+∠GEF=180°,∠FEH=∠1=35°,
∴∠GEF=180°−∠3=180°−165°=15°.
∵∠GEH=∠GEF+∠FEH=15°+35°=50°,
∴路政工程车的工作示意图中∠2的度数为50°.
50° [解析]工作篮底部AB与支撑平台CD平行,如图,过点E作EF//AB,

∴AB//EF//CD,
∴∠3+∠GEF=180°,∠FEH=∠1=35°,
∴∠GEF=180°−∠3=180°−165°=15°.
∵∠GEH=∠GEF+∠FEH=15°+35°=50°,
∴路政工程车的工作示意图中∠2的度数为50°.
5.(2025·广东深圳福田区期末)如图,∠BMD= ∠ABM+∠MDC.
(1)求证:AB//CD.
小颖同学是这样做的,请你将证明过程补充完整.
证明:如图(1),过点M作MP//AB,
(2)如图(2),若BN,DN分别平分∠ABM和∠MDC,则∠M与∠N之间的等量关系为______.

(1)求证:AB//CD.
小颖同学是这样做的,请你将证明过程补充完整.
证明:如图(1),过点M作MP//AB,
(2)如图(2),若BN,DN分别平分∠ABM和∠MDC,则∠M与∠N之间的等量关系为______.

答案:
(1)过点M作MP//AB,
∴∠ABM=∠BMQ.又∠BMD=∠ABM+∠MDC,∠BMD=∠BMQ+∠QMD,
∴∠MDC=∠QMD,
∴MQ//CD,
∴AB//CD.
(2)∠BMD=2∠BND [解析]如图,过点N作NE //AB,
∴∠ABN=∠BNE.同理,可得∠CDN=∠DNE.又∠BND=∠BNE+∠DNE,
∴∠BND=∠ABN+∠CDN.
∵BN,DN分别平分∠ABM和∠MDC,
∴∠ABM=2∠ABN,∠MDC=2∠CDN,
∴∠ABM+∠MDC=2∠ABN+2∠CDN=2∠BND.又∠BMD=∠ABM+∠MDC,
∴∠BMD=2∠BND.
(1)过点M作MP//AB,
∴∠ABM=∠BMQ.又∠BMD=∠ABM+∠MDC,∠BMD=∠BMQ+∠QMD,
∴∠MDC=∠QMD,
∴MQ//CD,
∴AB//CD.
(2)∠BMD=2∠BND [解析]如图,过点N作NE //AB,

∴∠ABN=∠BNE.同理,可得∠CDN=∠DNE.又∠BND=∠BNE+∠DNE,
∴∠BND=∠ABN+∠CDN.
∵BN,DN分别平分∠ABM和∠MDC,
∴∠ABM=2∠ABN,∠MDC=2∠CDN,
∴∠ABM+∠MDC=2∠ABN+2∠CDN=2∠BND.又∠BMD=∠ABM+∠MDC,
∴∠BMD=2∠BND.