6.(2024·山东泰安东平期末)已知,EF//AB,CD⊥DF,判断∠1,∠2,∠3之间的关系满足(

A.∠1+∠2+∠3= 180°
B.∠2= ∠3+∠1
C.∠1+∠2-∠3= 90°
D.∠2+∠3-∠1= 90°
C
). 
A.∠1+∠2+∠3= 180°
B.∠2= ∠3+∠1
C.∠1+∠2-∠3= 90°
D.∠2+∠3-∠1= 90°
答案:C
解析:
过点D作DG//EF,交AC于点G。
∵EF//AB,
∴DG//AB。
∴∠1=∠FDG,∠3=∠CDG。
∵CD⊥DF,
∴∠FDC=90°。
∵∠2=∠FDG+∠FDC-∠CDG=∠1+90°-∠3,
∴∠1+∠2-∠3=90°。
C
∵EF//AB,
∴DG//AB。
∴∠1=∠FDG,∠3=∠CDG。
∵CD⊥DF,
∴∠FDC=90°。
∵∠2=∠FDG+∠FDC-∠CDG=∠1+90°-∠3,
∴∠1+∠2-∠3=90°。
C
7.(2025·河南周口沈丘期末)如图,AB//CD,用含∠1,∠2,∠3的式子表示∠4,则∠4的值为( ).

A.∠1+∠2-∠3
B.∠1+∠3-∠2
C.180°+∠3-∠1-∠2
D.∠2+∠3-∠1-180°

A.∠1+∠2-∠3
B.∠1+∠3-∠2
C.180°+∠3-∠1-∠2
D.∠2+∠3-∠1-180°
答案:
D [解析]如图,过点E作EG//AB,过点F作FH//CD.
∵AB//CD,
∴AB//CD//EG//FH,
∴∠1=∠AEG,
∴∠GEF=∠2−∠1.
∵EG//FH,
∴∠EFH=180°−∠GEF=180°−(∠2−∠1)=180°−∠2+∠1,
∴∠CFH=∠3−∠EFH=∠3−(180°−∠2+∠1)=∠3+∠2−∠1−180°.
∵FH//CD,
∴∠4=∠3+∠2−∠1−180°.故选D.
D [解析]如图,过点E作EG//AB,过点F作FH//CD.
∵AB//CD,
∴AB//CD//EG//FH,
∴∠1=∠AEG,
∴∠GEF=∠2−∠1.
∵EG//FH,
∴∠EFH=180°−∠GEF=180°−(∠2−∠1)=180°−∠2+∠1,
∴∠CFH=∠3−∠EFH=∠3−(180°−∠2+∠1)=∠3+∠2−∠1−180°.
∵FH//CD,
∴∠4=∠3+∠2−∠1−180°.故选D.

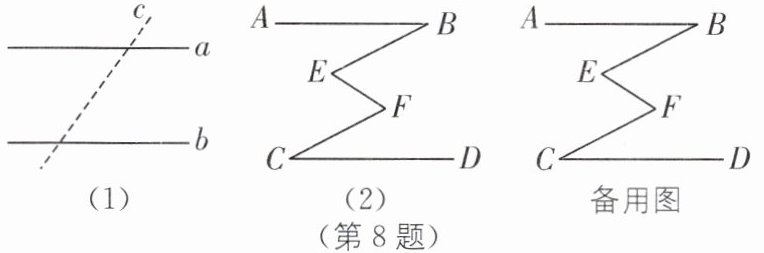
8.(2025·连云港期末)[阅读·领会]在几何图形学习过程中,为了帮助解题可在原图的基础上添加直线或线段,比如要证明直线a,b是否平行,可添加“第三条直线”(即图(1)中的截线c),把判断两条直线的位置关系转化为判断两个角的数量关系.我们称直线c为“辅助线”.
[实践·体悟]如图(2),已知∠ABE= ∠DCF,∠E= ∠F.求证:AB//CD.
(1)小明同学想到通过连接BC,作出平行线的截线,请你帮他完成下列证明过程:
证明:连接BC.
因为∠E= ∠F(已知),
所以______(内错角相等,两直线平行),
所以______(两直线平行,内错角相等).
因为∠ABE= ∠DCF(已知),
所以∠ABE+______= ∠DCF+______(等式性质),
所以______= ______(等量代换),
所以AB//CD(______).
(2)请你试用其他方法进行推理,并书写证明过程.
[实践·体悟]如图(2),已知∠ABE= ∠DCF,∠E= ∠F.求证:AB//CD.
(1)小明同学想到通过连接BC,作出平行线的截线,请你帮他完成下列证明过程:
证明:连接BC.
因为∠E= ∠F(已知),
所以______(内错角相等,两直线平行),
所以______(两直线平行,内错角相等).
因为∠ABE= ∠DCF(已知),
所以∠ABE+______= ∠DCF+______(等式性质),
所以______= ______(等量代换),
所以AB//CD(______).
(2)请你试用其他方法进行推理,并书写证明过程.

答案:
(1)BE//CF ∠EBC=∠FCB ∠EBC ∠FCB ∠ABC ∠DCB 内错角相等,两直线平行
(2)如图,延长BE交直线CD于点M.
∵∠BEF=∠F,
∴BM//CF,
∴∠BMC=∠DCF.
∵∠ABE=∠DCF,
∴∠BMC=∠ABE,
∴AB//CD.
(1)BE//CF ∠EBC=∠FCB ∠EBC ∠FCB ∠ABC ∠DCB 内错角相等,两直线平行
(2)如图,延长BE交直线CD于点M.

∵∠BEF=∠F,
∴BM//CF,
∴∠BMC=∠DCF.
∵∠ABE=∠DCF,
∴∠BMC=∠ABE,
∴AB//CD.