12. 已知线段$AB= 6\ cm$,延长AB到点C,使$BC= 4AB$,D为AB的中点,则线段$DC= $
27
cm.答案:27
解析:
因为$AB = 6\ cm$,$BC = 4AB$,所以$BC=4×6 = 24\ cm$。
因为$D$为$AB$的中点,所以$AD=DB=\dfrac{1}{2}AB=\dfrac{1}{2}×6 = 3\ cm$。
因为点$C$在$AB$的延长线上,所以$DC=DB + BC=3 + 24=27\ cm$。
27
因为$D$为$AB$的中点,所以$AD=DB=\dfrac{1}{2}AB=\dfrac{1}{2}×6 = 3\ cm$。
因为点$C$在$AB$的延长线上,所以$DC=DB + BC=3 + 24=27\ cm$。
27
13. 计算:$180^\circ - 25^\circ 28' - 77^\circ 36'= $
76°56′
.答案:76°56′ [解析]180° - 25°28′ - 77°36′ = 154°32′ - 77°36′ = 153°92′ - 77°36′ = 76°56′
解析:
180° - 25°28' - 77°36' = 154°32' - 77°36' = 153°92' - 77°36' = 76°56'
14. 某校九年级在下午3:30开展“阳光体育”活动.下午3:30这一时刻,时钟上分针与时针所夹的角等于
75
度.答案:75 [解析]3:30,时针和分针中间相差2.5个大格.
∵钟表上有12个数字,每相邻两个数字之间的夹角为30°,
∴下午3:30分针与时针的夹角是2.5×30° = 75°
∵钟表上有12个数字,每相邻两个数字之间的夹角为30°,
∴下午3:30分针与时针的夹角是2.5×30° = 75°
15. 如图,直线AB,CD相交于点O,$EO \perp OF$,且OC平分$\angle AOE$,若$\angle BOF= 38^\circ$,则$\angle DOF= $
26
°.答案:26 [解析]
∵OE⊥OF,
∴∠EOF = 90°.
∵∠BOF = 38°,
∴∠BOE = 90° - 38° = 52°.
∴∠AOE = 180° - ∠BOE = 180° - 52° = 128°.又OC平分∠AOE,
∴∠AOC = $\frac{1}{2}$∠AOE = $\frac{1}{2}$×128° = 64°.
∵∠BOD和∠AOC互为对顶角,
∴∠BOD = ∠AOC = 64°.
∴∠DOF = ∠BOD - ∠BOF = 64° - 38° = 26°.
∵OE⊥OF,
∴∠EOF = 90°.
∵∠BOF = 38°,
∴∠BOE = 90° - 38° = 52°.
∴∠AOE = 180° - ∠BOE = 180° - 52° = 128°.又OC平分∠AOE,
∴∠AOC = $\frac{1}{2}$∠AOE = $\frac{1}{2}$×128° = 64°.
∵∠BOD和∠AOC互为对顶角,
∴∠BOD = ∠AOC = 64°.
∴∠DOF = ∠BOD - ∠BOF = 64° - 38° = 26°.
16. (2025·济南钢城区一模)已知直线$m // n$,将一块含$30^\circ$角的直角三角板ABC按如图方式放置($\angle ABC= 30^\circ$),其中A,B两点分别落在直线m,n上,若$\angle 1= 20^\circ$,则$\angle 2$的度数为
50
°.答案:50
解析:
过点C作CD//m,
因为m//n,所以CD//n,
所以∠ACD=∠2,∠BCD=∠1=20°,
因为∠ABC=30°,△ABC是直角三角形,
所以∠ACB=90°-30°=60°,
所以∠ACD=∠ACB-∠BCD=60°-20°=40°,
所以∠2=40°。
答案:40
因为m//n,所以CD//n,
所以∠ACD=∠2,∠BCD=∠1=20°,
因为∠ABC=30°,△ABC是直角三角形,
所以∠ACB=90°-30°=60°,
所以∠ACD=∠ACB-∠BCD=60°-20°=40°,
所以∠2=40°。
答案:40
17. 如图,在四边形ABCD中,$AB // CD$,$AD // BC$,$\angle 1$是四边形ABCD的一个外角.若$\angle 1= 72^\circ$,则$\angle C= $
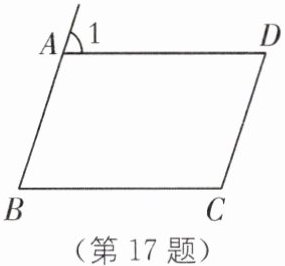
108
°.
答案:108
解析:
因为$AB // CD$,$AD // BC$,所以四边形$ABCD$是平行四边形。
在平行四边形中,$\angle DAB = \angle C$。
因为$\angle 1$是四边形$ABCD$的一个外角,且$\angle 1$与$\angle DAB$互为邻补角,所以$\angle 1 + \angle DAB = 180^\circ$。
已知$\angle 1 = 72^\circ$,则$\angle DAB = 180^\circ - 72^\circ = 108^\circ$,所以$\angle C = 108^\circ$。
$108$
在平行四边形中,$\angle DAB = \angle C$。
因为$\angle 1$是四边形$ABCD$的一个外角,且$\angle 1$与$\angle DAB$互为邻补角,所以$\angle 1 + \angle DAB = 180^\circ$。
已知$\angle 1 = 72^\circ$,则$\angle DAB = 180^\circ - 72^\circ = 108^\circ$,所以$\angle C = 108^\circ$。
$108$
18. 如图,已知$\angle AOB= 150^\circ$,$\angle COD= 40^\circ$,$\angle COD在\angle AOB$的内部绕点O任意旋转,若OE平分$\angle AOC$($\angle AOE>40^\circ$),则$2\angle BOE - \angle BOD$的值为______°.


答案:
110 [解析]如图,
∵OE平分∠AOC,
∴∠AOE = ∠COE.设∠DOE = x,
∵∠COD = 40°,
∴∠AOE = ∠COE = x + 40°.
∴∠BOC = ∠AOB - ∠AOC = 150° - 2(x + 40°) = 70° - 2x.
∴2∠BOE - ∠BOD = 2(70° - 2x + 40° + x) - (70° - 2x + 40°) = 140° - 4x + 80° + 2x - 70° + 2x - 40° = 110°.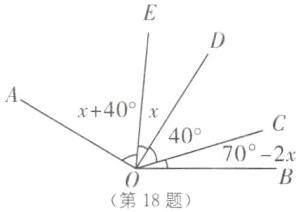
110 [解析]如图,
∵OE平分∠AOC,
∴∠AOE = ∠COE.设∠DOE = x,
∵∠COD = 40°,
∴∠AOE = ∠COE = x + 40°.
∴∠BOC = ∠AOB - ∠AOC = 150° - 2(x + 40°) = 70° - 2x.
∴2∠BOE - ∠BOD = 2(70° - 2x + 40° + x) - (70° - 2x + 40°) = 140° - 4x + 80° + 2x - 70° + 2x - 40° = 110°.

19. 如图,平面内有三个点A,B,C,按要求完成下列问题:
(1)在图中画出直线AB、射线AC、线段BC.
(2)观察图形发现,线段$AB + BC>AC$,得出这个结论的依据是______.
(3)平面内是否存在点D,使得$AD - BD= AB$?如果存在,在图中画出一个满足条件的点D;如果不存在,说明理由.

(1)在图中画出直线AB、射线AC、线段BC.
(2)观察图形发现,线段$AB + BC>AC$,得出这个结论的依据是______.
(3)平面内是否存在点D,使得$AD - BD= AB$?如果存在,在图中画出一个满足条件的点D;如果不存在,说明理由.

答案:
(1)如图
(1)所示:
(2)两点之间,线段最短
(3)平面内存在点D,使得AD - BD = AB,如图
(2)所示,当点D与B重合或在线段AB的延长线上时,满足条件,
(1)如图
(1)所示:

(2)两点之间,线段最短
(3)平面内存在点D,使得AD - BD = AB,如图
(2)所示,当点D与B重合或在线段AB的延长线上时,满足条件,

20. (2024·自贡中考改编)如图,在$\triangle ABC$中,$DE // BC$,$\angle EDF= \angle C$.试说明:$\angle BDF= \angle A$.


答案:
∵DE//BC,
∴∠C = ∠AED.
∵∠EDF = ∠C,
∴∠AED = ∠EDF,
∴DF//AC,
∴∠BDF = ∠A.
∵DE//BC,
∴∠C = ∠AED.
∵∠EDF = ∠C,
∴∠AED = ∠EDF,
∴DF//AC,
∴∠BDF = ∠A.
21. 如图,点C在线段AB上,图中共有三条线段AB,AC和BC,若其中有一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“巧点”.
(1)线段的中点______这条线段的“巧点”;(填“是”或“不是”)
(2)若$AB= 12\ cm$,点C是线段AB的巧点,求AC的长.

(1)线段的中点______这条线段的“巧点”;(填“是”或“不是”)
(2)若$AB= 12\ cm$,点C是线段AB的巧点,求AC的长.

答案:
(1)是 [解析]如图,当点C是线段AB的中点时,则AB = 2AC,
∴线段的中点是这条线段的“巧点”
(2)
∵AB = 12cm,点C是线段AB的巧点,
∴AC = 12×$\frac{1}{3}$ = 4(cm)或AC = 12×$\frac{1}{2}$ = 6(cm)或AC = 12×$\frac{2}{3}$ = 8(cm).故AC的长为4cm或6cm或8cm.
(1)是 [解析]如图,当点C是线段AB的中点时,则AB = 2AC,

∴线段的中点是这条线段的“巧点”
(2)
∵AB = 12cm,点C是线段AB的巧点,
∴AC = 12×$\frac{1}{3}$ = 4(cm)或AC = 12×$\frac{1}{2}$ = 6(cm)或AC = 12×$\frac{2}{3}$ = 8(cm).故AC的长为4cm或6cm或8cm.