15. (2025·扬州江都区邵樊片期中)我们规定关于x的一元一次方程ax= b的解为x= b-a,则称该方程是“差解方程”,例如:3x= 4.5的解为x= 4.5-3= 1.5,则该方程3x= 4.5就是“差解方程”,请根据上述规定解答下列问题:
[定义理解]
(1)判断:方程2x= 4______差解方程;(填“是”或“不是”)
(2)若关于x的一元一次方程4x= m是“差解方程”,求m的值;
[知识应用]
(3)已知关于x的一元一次方程4x= ab+a是“差解方程”,则3(ab+a)= ______;
(4)已知关于x的一元一次方程4x= mn+m和-2x= mn+n都是“差解方程”,求代数式$3(mn+m)-9(mn+n)^2$的值.
(1)
(2)m=$\frac{16}{3}$
(3)
(4)
[定义理解]
(1)判断:方程2x= 4______差解方程;(填“是”或“不是”)
(2)若关于x的一元一次方程4x= m是“差解方程”,求m的值;
[知识应用]
(3)已知关于x的一元一次方程4x= ab+a是“差解方程”,则3(ab+a)= ______;
(4)已知关于x的一元一次方程4x= mn+m和-2x= mn+n都是“差解方程”,求代数式$3(mn+m)-9(mn+n)^2$的值.
(1)
是
(2)m=$\frac{16}{3}$
(3)
16
(4)
0
答案:
(1)是 [解析]
∵方程2x=4的解为x=2=4-2,
∴方程2x=4是差解方程.
(2)由题意可知x=m-4,由一元一次方程可知x=$\frac{m}{4}$,
∴m-4=$\frac{m}{4}$,解得m=$\frac{16}{3}$.
(3)16 [解析]
∵方程4x=ab+a是“差解方程”,
∴x=ab+a-4.解方程4x=ab+a,得x=$\frac{ab+a}{4}$,
∴ab+a-4=$\frac{ab+a}{4}$,
∴3ab+3a=16,即3(ab+a)=16.
(4)
∵一元一次方程4x=mn+m是“差解方程”,
∴x=mn+m-4.解一元一次方程4x=mn+m得x=$\frac{mn+m}{4}$,
∴mn+m-4=$\frac{mn+m}{4}$,整理得3(mn+m)=16.
∵一元一次方程-2x=mn+n是“差解方程”,
∴x=mn+n+2,解一元一次方程-2x=mn+n得x=-$\frac{mn+n}{2}$.
∴mn+n+2=-$\frac{mn+n}{2}$,整理得9(mn+n)²=16,
∴3(mn+m)-9(mn+n)²=16-16 =0.
(1)是 [解析]
∵方程2x=4的解为x=2=4-2,
∴方程2x=4是差解方程.
(2)由题意可知x=m-4,由一元一次方程可知x=$\frac{m}{4}$,
∴m-4=$\frac{m}{4}$,解得m=$\frac{16}{3}$.
(3)16 [解析]
∵方程4x=ab+a是“差解方程”,
∴x=ab+a-4.解方程4x=ab+a,得x=$\frac{ab+a}{4}$,
∴ab+a-4=$\frac{ab+a}{4}$,
∴3ab+3a=16,即3(ab+a)=16.
(4)
∵一元一次方程4x=mn+m是“差解方程”,
∴x=mn+m-4.解一元一次方程4x=mn+m得x=$\frac{mn+m}{4}$,
∴mn+m-4=$\frac{mn+m}{4}$,整理得3(mn+m)=16.
∵一元一次方程-2x=mn+n是“差解方程”,
∴x=mn+n+2,解一元一次方程-2x=mn+n得x=-$\frac{mn+n}{2}$.
∴mn+n+2=-$\frac{mn+n}{2}$,整理得9(mn+n)²=16,
∴3(mn+m)-9(mn+n)²=16-16 =0.
16. (2025·南通启东长江中学月考)[阅读理解]我们经常过某个点作已知直线的平行线,以便利用平行线的性质来解决问题.例如:如图(1),已知AB//CD,点E,F分别在直线AB,CD上,点P在直线AB,CD之间.设∠AEP= ∠α,∠CFP= ∠β.求证:∠P= ∠α+∠β.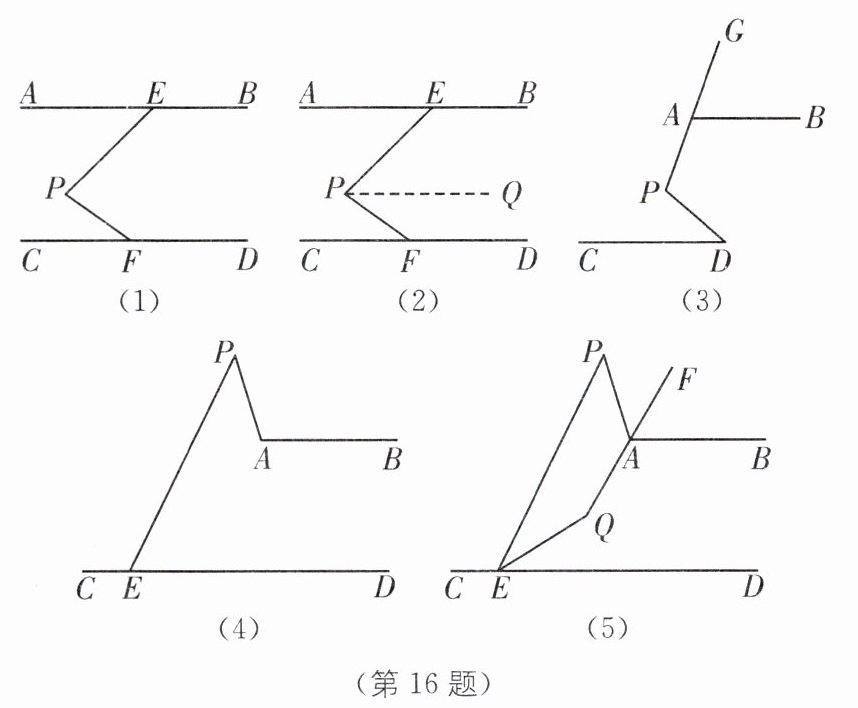
证明:如图(2),过点P作PQ//AB,∴∠EPQ= ∠AEP= ∠α,∵PQ//AB,AB//CD,∴PQ//CD,∴∠FPQ= ∠CFP= ∠β.∴∠EPF= ∠EPQ+∠FPQ= ∠α+∠β,即∠EPF= ∠α+∠β.可以运用以上结论解答下列问题:
[类比应用]
(1)如图(3),已知AB//CD,∠D= 15°,∠GAB= 70°,求∠P的度数.
(2)如图(4),已知AB//CD,点E在直线CD上,点P在直线AB上方,连接PA,PE,则∠PAB,∠CEP,∠APE之间有何数量关系?请说明理由.
[拓展应用]
(3)如图(5),已知AB//CD,点E在直线CD上,点P在直线AB上方,连接PA,PE,∠PED的平分线与∠PAB的平分线所在直线交于点Q,求∠APE+2∠AQE的值.

证明:如图(2),过点P作PQ//AB,∴∠EPQ= ∠AEP= ∠α,∵PQ//AB,AB//CD,∴PQ//CD,∴∠FPQ= ∠CFP= ∠β.∴∠EPF= ∠EPQ+∠FPQ= ∠α+∠β,即∠EPF= ∠α+∠β.可以运用以上结论解答下列问题:
[类比应用]
(1)如图(3),已知AB//CD,∠D= 15°,∠GAB= 70°,求∠P的度数.
(2)如图(4),已知AB//CD,点E在直线CD上,点P在直线AB上方,连接PA,PE,则∠PAB,∠CEP,∠APE之间有何数量关系?请说明理由.
[拓展应用]
(3)如图(5),已知AB//CD,点E在直线CD上,点P在直线AB上方,连接PA,PE,∠PED的平分线与∠PAB的平分线所在直线交于点Q,求∠APE+2∠AQE的值.
答案:
(1)如图
(1),延长BA至点H.
∵AB//CD,
∴∠APD=∠HAP+∠D,
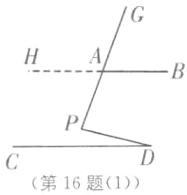
∵∠HAP=∠GAB,∠GAB =70°,
∴∠HAP=70°.
∵∠D=15°,
∴∠APD=85°.
(2)∠CEP+∠PAB-∠APE=180°,理由如下:如图
(2),过点P作PM//AB,
∵AB//CD,
∴AB//CD//PM,
∴∠MPE=∠CEP,
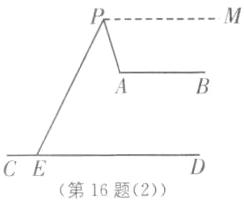
∠MPA+∠PAB=180°,
∴∠MPE-∠MPA-∠PAB=∠CEP-180°,即∠APE-∠PAB=∠CEP-180°,
∴∠CEP+∠PAB-∠APE=180°.
(3)由示例知,
∵AB//CD,
∴∠AQE=∠BAQ+∠DEQ,
∴2∠AQE=2∠BAQ+2∠DEQ=2(180°-∠BAF)+2∠DEQ.

∵QE,AF分别是∠PED与∠PAB的平分线,
∴2∠BAF=∠PAB,2∠DEQ=∠PED,
∴2∠AQE=360°-∠PAB+∠PED.由
(2)知∠CEP+∠PAB-∠APE=180°,
∴∠APE=∠CEP+∠PAB-180°,
∴2∠AQE+∠APE=360°-∠PAB+∠PED+∠CEP+∠PAB-180°=180°+180°=360°,即2∠AQE+∠APE=360°.
(1)如图
(1),延长BA至点H.
∵AB//CD,
∴∠APD=∠HAP+∠D,

∵∠HAP=∠GAB,∠GAB =70°,
∴∠HAP=70°.
∵∠D=15°,
∴∠APD=85°.
(2)∠CEP+∠PAB-∠APE=180°,理由如下:如图
(2),过点P作PM//AB,
∵AB//CD,
∴AB//CD//PM,
∴∠MPE=∠CEP,

∠MPA+∠PAB=180°,
∴∠MPE-∠MPA-∠PAB=∠CEP-180°,即∠APE-∠PAB=∠CEP-180°,
∴∠CEP+∠PAB-∠APE=180°.
(3)由示例知,
∵AB//CD,
∴∠AQE=∠BAQ+∠DEQ,
∴2∠AQE=2∠BAQ+2∠DEQ=2(180°-∠BAF)+2∠DEQ.

∵QE,AF分别是∠PED与∠PAB的平分线,
∴2∠BAF=∠PAB,2∠DEQ=∠PED,
∴2∠AQE=360°-∠PAB+∠PED.由
(2)知∠CEP+∠PAB-∠APE=180°,
∴∠APE=∠CEP+∠PAB-180°,
∴2∠AQE+∠APE=360°-∠PAB+∠PED+∠CEP+∠PAB-180°=180°+180°=360°,即2∠AQE+∠APE=360°.