1. 李老师在生物实验室做实验时,将水稻种子分组进行发芽实验.第1组取3粒,第2组取5粒,第3组取7粒……即每组所取种子数目比该组前一组增加2粒,按此规律,推测第7组应取种子粒数为(
A.15
B.13
C.14
D.9
A
).A.15
B.13
C.14
D.9
答案:A
解析:
第1组:3粒
第2组:3+2=5粒
第3组:5+2=7粒
规律:每组种子数=3+2×(组号-1)
第7组:3+2×(7-1)=3+12=15粒
A
第2组:3+2=5粒
第3组:5+2=7粒
规律:每组种子数=3+2×(组号-1)
第7组:3+2×(7-1)=3+12=15粒
A
2. 传统文化 杨辉三角 如图在我国宋朝数学家杨辉1261年的著作《详解九章算法》中提到过,因而人们把这个表叫作杨辉三角,根据杨辉三角的规律,表第四行空缺的数字是
3
.答案:3
3. (2025·连云港期中)我国民间通常用12种动物(十二生肖)来表示不同的年份.它们排列顺序如下:鼠,牛,虎,兔,龙,蛇,马,羊,猴,鸡,狗,猪,2024年是龙年,那么2049年是
蛇
年.答案:蛇
解析:
2049-2024=25
25÷12=2……1
龙年之后第1年是蛇年
蛇
25÷12=2……1
龙年之后第1年是蛇年
蛇
4. 观察下列等式:$\frac{3}{1×4}= 1-\frac{1}{4}$,$\frac{3}{4×7}= \frac{1}{4}-\frac{1}{7}$,$\frac{3}{7×10}= \frac{1}{7}-\frac{10}{10}$,$\frac{3}{10×13}= \frac{1}{10}-\frac{1}{13}$,…,求$\frac{1}{1×4}+\frac{1}{4×7}+\frac{1}{7×10}+\frac{1}{10×13}+…+\frac{1}{100×103}$的值.
答案:原式$=\frac{1}{3}×(1-\frac{1}{4}+\frac{1}{4}-\frac{1}{7}+\frac{1}{7}-\frac{1}{10}+\frac{1}{10}-\frac{1}{13}+\cdots +\frac{1}{100}-\frac{1}{103})=\frac{1}{3}×(1-\frac{1}{103})=\frac{1}{3}×\frac{102}{103}=\frac{34}{103}$
5. 数学文化 “正方形数” 古希腊著名的毕达哥拉斯学派把1,3,6,10,…,这样的数称为“三角形数”,而把1,4,9,16,…,这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.下列等式中,符合这一规律的是(
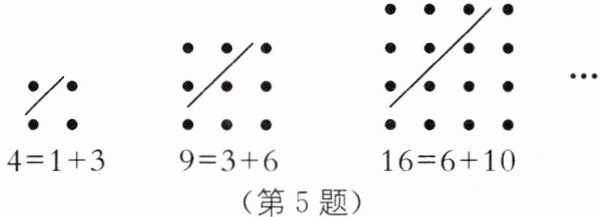
A.20= 4+16
B.25= 9+16
C.36= 15+21
D.40= 12+28
C
).
A.20= 4+16
B.25= 9+16
C.36= 15+21
D.40= 12+28
答案:C
解析:
三角形数规律:第$n$个三角形数为$\frac{n(n + 1)}{2}$。
正方形数规律:第$m$个正方形数为$m^2$。
规律:$m^2=\frac{(m - 1)m}{2}+\frac{m(m + 1)}{2}$。
A. 20不是正方形数,不符合。
B. 25是$5^2$,$\frac{4×5}{2}=10$,$\frac{5×6}{2}=15$,$10 + 15=25\neq9 + 16$,不符合。
C. 36是$6^2$,$\frac{5×6}{2}=15$,$\frac{6×7}{2}=21$,$15 + 21=36$,符合。
D. 40不是正方形数,不符合。
答案:C
正方形数规律:第$m$个正方形数为$m^2$。
规律:$m^2=\frac{(m - 1)m}{2}+\frac{m(m + 1)}{2}$。
A. 20不是正方形数,不符合。
B. 25是$5^2$,$\frac{4×5}{2}=10$,$\frac{5×6}{2}=15$,$10 + 15=25\neq9 + 16$,不符合。
C. 36是$6^2$,$\frac{5×6}{2}=15$,$\frac{6×7}{2}=21$,$15 + 21=36$,符合。
D. 40不是正方形数,不符合。
答案:C
6. 实验班原创 观察并找规律:$2^{1}= 2$,$2^{2}= 4$,$2^{3}= 8$,$2^{4}= 16$,$2^{5}= 32$,$2^{6}= 64$,$2^{7}= 128$,$2^{8}= 256$,那么$2^{2025}$的个位数是(
A.2
B.4
C.6
D.8
A
).A.2
B.4
C.6
D.8
答案:A [解析]$\because 2^{1},2^{3},2^{3},2^{4},\cdots ,2^{2025}$个位数字是2,4,8,6四个一循环,又$2025÷4=506\cdots\cdots1$,$\therefore 2^{2025}$的个位数字应该是2.故选A.
7. 教材P9练习·变式 观察如图所示的图形:

它们是按一定规律排列的,依照此规律,第2025个图形中共有

它们是按一定规律排列的,依照此规律,第2025个图形中共有
6076
个.答案:6076
解析:
第1个图形有4个★,第2个图形有7个★,第3个图形有10个★,第4个图形有13个★,规律为第$n$个图形有$(3n + 1)$个★。当$n = 2025$时,$3×2025 + 1 = 6076$。
6076
6076
8. 如图,按照图(1)、图(2)、图(3)的数字规律,则图(4)的括号中应填数字为______.
10
答案:10 [解析]由题意,得两个圆圈中的数之和的2倍等于左、右两个数的乘积,所以题图
(4)的括号中应填数字为$(15+15)×2÷6=10$. 解后反思 本题考查数字的变化规律,通过观察能够发现给出的四个数之间的联系是解题的关键.
(4)的括号中应填数字为$(15+15)×2÷6=10$. 解后反思 本题考查数字的变化规律,通过观察能够发现给出的四个数之间的联系是解题的关键.