7. 已知甲、乙两人在一个200米的环形跑道上练习跑步,现在把跑道分成相等的4段,即两条直道和两条弯道的长度相同. 甲平均每秒跑4米,乙平均每秒跑6米,若甲、乙两人分别从A,C两处同时相向出发(如图所示),试解答下列问题:
(1)几秒后两人首次相遇? 此时他们在哪段跑道上?
(2)首次相遇后,又经过多长时间他们再次相遇? 在哪一段跑道上?
(3)他们第10次相遇时,在哪一段跑道上?
(4)若甲、乙两人在首次相遇后,甲、乙两人决定同方向练习跑步,问:甲、乙两人经过多长时间再次相遇? 在哪一段跑道上?
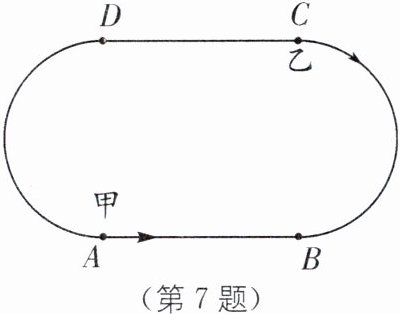
(1)几秒后两人首次相遇? 此时他们在哪段跑道上?
(2)首次相遇后,又经过多长时间他们再次相遇? 在哪一段跑道上?
(3)他们第10次相遇时,在哪一段跑道上?
(4)若甲、乙两人在首次相遇后,甲、乙两人决定同方向练习跑步,问:甲、乙两人经过多长时间再次相遇? 在哪一段跑道上?

答案:
(1)设x秒后两人首次相遇,
由题意,得4x+6x=100,解得x=10,
甲跑的路程为4×10=40(米).
故10秒后两人首次相遇,此时他们在直道AB上,且距离点B10米的位置.
(2)设y秒后两人再次相遇,
由题意,得4y+6y=200,解得y=20,
首次相遇后,甲跑的路程为4×20=80(米).
故20秒后两人再次相遇,此时他们在直道CD上,且距离点D30米的位置.
(3)第1次相遇,总用时10秒;
第2次相遇,总用时10+20×1=30(秒);
第3次相遇,总用时10+20×2=50(秒);
…
第10次相遇,总用时10+20×9=190(秒).
此时甲跑的圈数为190×4÷200=3.8.
∵200×(3.8-3)=160(米),
∴此时甲在弯道AD上,且距离点A40米的位置.
(4)甲、乙两人经过z秒再次相遇,
由题意,得6z-4z=200,解得z=100,
故100秒后再次相遇,甲跑的路程为4×100=400(米).
故甲在他们第一次相遇后又跑了2圈,此时他们在直道AB上,且距离点B10米的位置.
思路引导 本题考查的是一元一次方程中的行程问题,解题的关键是理解相遇问题以及找到第10次相遇时用的时间为多少,通过构建数学模型求解.
(1)设x秒后两人首次相遇,
由题意,得4x+6x=100,解得x=10,
甲跑的路程为4×10=40(米).
故10秒后两人首次相遇,此时他们在直道AB上,且距离点B10米的位置.
(2)设y秒后两人再次相遇,
由题意,得4y+6y=200,解得y=20,
首次相遇后,甲跑的路程为4×20=80(米).
故20秒后两人再次相遇,此时他们在直道CD上,且距离点D30米的位置.
(3)第1次相遇,总用时10秒;
第2次相遇,总用时10+20×1=30(秒);
第3次相遇,总用时10+20×2=50(秒);
…
第10次相遇,总用时10+20×9=190(秒).
此时甲跑的圈数为190×4÷200=3.8.
∵200×(3.8-3)=160(米),
∴此时甲在弯道AD上,且距离点A40米的位置.
(4)甲、乙两人经过z秒再次相遇,
由题意,得6z-4z=200,解得z=100,
故100秒后再次相遇,甲跑的路程为4×100=400(米).
故甲在他们第一次相遇后又跑了2圈,此时他们在直道AB上,且距离点B10米的位置.
思路引导 本题考查的是一元一次方程中的行程问题,解题的关键是理解相遇问题以及找到第10次相遇时用的时间为多少,通过构建数学模型求解.
8. (2024·威海中考改编)定义:我们把数轴上表示数a的点与原点的距离叫作数a的绝对值. 数轴上表示数a,b的点A,B之间的距离AB= a-b(a≥b). 特别的,当a≥0时,表示数a的点与原点的距离等于a-0;当a<0时,表示数a的点与原点的距离等于0-a.
应用:如图,在数轴上,动点A从表示-3的点出发,以1个单位/秒的速度沿着数轴的正方向运动. 同时,动点B从表示12的点出发,以2个单位/秒的速度沿着数轴的负方向运动. 问经过多长时间,点A,B之间的距离等于3个单位长度?

应用:如图,在数轴上,动点A从表示-3的点出发,以1个单位/秒的速度沿着数轴的正方向运动. 同时,动点B从表示12的点出发,以2个单位/秒的速度沿着数轴的负方向运动. 问经过多长时间,点A,B之间的距离等于3个单位长度?

答案:设经过m秒,点A,B之间的距离等于3个单位长度,
则|(-3+m)-(12-2m)|=3,
解得m=4或m=6.
故经过4秒或6秒,点A,B之间的距离等于3个单位长度.
则|(-3+m)-(12-2m)|=3,
解得m=4或m=6.
故经过4秒或6秒,点A,B之间的距离等于3个单位长度.