1. 教材P128练习T1·拓展(2024·广东茂名高州期末)墙上钉着用一根彩绳围成的梯形形状的饰物,如图实线所示(单位:cm).小颖将梯形下底的钉子去掉,并将这条彩绳钉成一个长方形,如图虚线所示.小颖所钉长方形的长、宽各为多少厘米?如果设长方形的长为x cm,根据题意,可得方程为(
A.2(x+10)= 10×4+6×2
B.2(x+10)= 10×3+6×2
C.2x+10= 10×4+6×2
D.2(x+10)= 10×2+6×2
A
).A.2(x+10)= 10×4+6×2
B.2(x+10)= 10×3+6×2
C.2x+10= 10×4+6×2
D.2(x+10)= 10×2+6×2
答案:A
解析:
彩绳长度不变,即梯形周长等于长方形周长。
梯形各边长度:上底10cm,两腰各10cm,下底由6cm、10cm、6cm组成,下底长为$6 + 10 + 6=22$cm。
梯形周长为$10 + 10 + 10 + 22=52$cm。
长方形宽为10cm,长为$x$cm,周长为$2(x + 10)$。
可得方程:$2(x + 10)=52$,其中$52 = 10×4 + 6×2$($10×4$为上底与两腰及下底中间10cm部分,$6×2$为下底两侧6cm部分)。
A
梯形各边长度:上底10cm,两腰各10cm,下底由6cm、10cm、6cm组成,下底长为$6 + 10 + 6=22$cm。
梯形周长为$10 + 10 + 10 + 22=52$cm。
长方形宽为10cm,长为$x$cm,周长为$2(x + 10)$。
可得方程:$2(x + 10)=52$,其中$52 = 10×4 + 6×2$($10×4$为上底与两腰及下底中间10cm部分,$6×2$为下底两侧6cm部分)。
A
2. 一圆柱形容器的内半径为3厘米,内壁高30厘米,容器内盛有18厘米高的水,现将一个底面半径为2厘米,高15厘米的金属圆柱竖直放入容器内,则容器内的水将升高
$\frac{20}{3}$
厘米.答案:$\frac{20}{3}$
解析:
设容器内的水将升高$x$厘米。
金属圆柱放入容器后,水未溢出时,水面高度为$(18 + x)$厘米。
此时,水的体积加上金属圆柱浸入水中的体积等于容器内底面积乘以新水面高度。
金属圆柱的高为15厘米,因为$18 + x \leq 15$不成立,所以金属圆柱完全浸入水中。
根据体积关系可得:
$\pi × 3^2 × 18 + \pi × 2^2 × 15 = \pi × 3^2 × (18 + x)$
化简得:
$9\pi × 18 + 4\pi × 15 = 9\pi × (18 + x)$
$162\pi + 60\pi = 162\pi + 9\pi x$
$222\pi - 162\pi = 9\pi x$
$60\pi = 9\pi x$
$x = \frac{60}{9} = \frac{20}{3}$
$\frac{20}{3}$
金属圆柱放入容器后,水未溢出时,水面高度为$(18 + x)$厘米。
此时,水的体积加上金属圆柱浸入水中的体积等于容器内底面积乘以新水面高度。
金属圆柱的高为15厘米,因为$18 + x \leq 15$不成立,所以金属圆柱完全浸入水中。
根据体积关系可得:
$\pi × 3^2 × 18 + \pi × 2^2 × 15 = \pi × 3^2 × (18 + x)$
化简得:
$9\pi × 18 + 4\pi × 15 = 9\pi × (18 + x)$
$162\pi + 60\pi = 162\pi + 9\pi x$
$222\pi - 162\pi = 9\pi x$
$60\pi = 9\pi x$
$x = \frac{60}{9} = \frac{20}{3}$
$\frac{20}{3}$
3. 方程思想 如图,小明将一个正方形纸片剪去一个宽为4的长条后,再从剩下的长方形纸片上剪去一个宽为5的长条.如果两次剪下的长条面积正好相等,那么每一个长条的面积是多少?
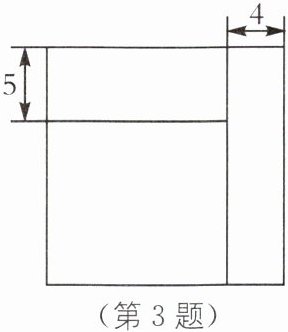

答案:设正方形的边长是x.由题意,得4x=5(x - 4),解得x = 20,则4x = 80.故每一个长条的面积是80.
4. (2025·南通如皋期末)在数学活动课上,小华把一张白卡纸画出如图(1)所示的8个一样大小的长方形,再把这8个长方形纸片剪开,无重叠地拼成如图(2)的正方形ABCD,若中间小正方形的边长为3,则图(2)中大正方形的周长为
132
.答案:132 [解析]设小长方形的长为x,则宽为$\frac{3}{5}x$.由题图
(1),可知小长方形的长:宽 = 3:5
∵中间小正方形的边长为3,
∴$2×\frac{3}{5}x - x = 3$,解得x = 15,则$\frac{3}{5}x = 9$,所以正方形ABCD的周长是$4(x + 2×\frac{3}{5}x)=4×(15 + 18)=132$.
(1),可知小长方形的长:宽 = 3:5
∵中间小正方形的边长为3,
∴$2×\frac{3}{5}x - x = 3$,解得x = 15,则$\frac{3}{5}x = 9$,所以正方形ABCD的周长是$4(x + 2×\frac{3}{5}x)=4×(15 + 18)=132$.
5. 新情境 乌鸦喝水 (2025·连云港期末)我们都知道《乌鸦喝水》的故事,聪明的乌鸦衔来一个个小石子放入瓶中,水位上升后,喝到了水.根据图中给出的信息,解答下列问题:(温馨提示:仔细看图,玻璃桶高65 cm,桶内液面原来高度为26 cm)
(1)放入一个小球水面升高
(2)如果放入大球、小球共10个,且使水面恰好上升到61厘米,应放入大球、小球各多少个?
(1)放入一个小球水面升高
3
cm,放入一个大球水面升高4
cm.(2)如果放入大球、小球共10个,且使水面恰好上升到61厘米,应放入大球、小球各多少个?
设应放入大球m个,则放入小球(10 - m)个,由题意,得4m + 3(10 - m)=61 - 26,解得m = 5.所以10 - m = 10 - 5 = 5,故应放入大球5个,小球5个.
答案:
(1)3 4 [解析]设一个小球使水面升高x厘米,由题意,得3x = 35 - 26,解得x = 3.设一个大球使水面升高y厘米,由题意,得2y = 34 - 26,解得y = 4.所以放入一个小球水面升高3cm,放入一个大球水面升高4cm.
(2)设应放入大球m个,则放入小球(10 - m)个,由题意,得4m + 3(10 - m)=61 - 26,解得m = 5.所以10 - m = 10 - 5 = 5,故应放入大球5个,小球5个.
(1)3 4 [解析]设一个小球使水面升高x厘米,由题意,得3x = 35 - 26,解得x = 3.设一个大球使水面升高y厘米,由题意,得2y = 34 - 26,解得y = 4.所以放入一个小球水面升高3cm,放入一个大球水面升高4cm.
(2)设应放入大球m个,则放入小球(10 - m)个,由题意,得4m + 3(10 - m)=61 - 26,解得m = 5.所以10 - m = 10 - 5 = 5,故应放入大球5个,小球5个.