6. (2025·镇江丹徒期末)根据以下信息,探索并完成任务.
|现有一块长方形宣传牌,拟在上面书写24字宣传语.|
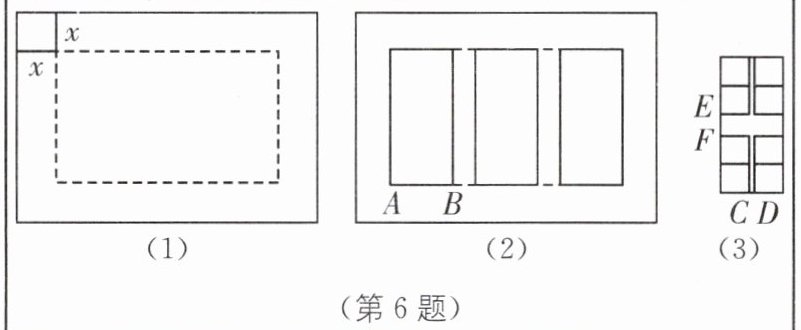
|信息1|如图(1),(1)实线部分是长方形宣传牌,长414 cm,宽270 cm；(2)中间虚线部分也是长方形,长是宽的1.6倍,用来设计；(3)四周空白部分的宽度相等.|
|信息2|如图(2),为了美观,将设计部分分割成大小相等的左中右三个长方形栏目,每个栏目书写8个字,栏目与栏目之间的中缝间距相等.|
|信息3|如图(3),每个栏目划出正方形方格,中间有十字间隔,竖向两列中间间隔(如CD)和横向中间间隔(如EF)宽度比为1∶2.|
|问题解决|
|任务1|设四周宽度为x cm,用含x的代数式分别表示设计部分的长和宽.|
|任务2|求四周宽度x的值.|
|任务3|(1)求每个栏目的水平宽度(如AB)；(2)求长方形栏目与栏目之间中缝的间距.|
|现有一块长方形宣传牌,拟在上面书写24字宣传语.|
|信息1|如图(1),(1)实线部分是长方形宣传牌,长414 cm,宽270 cm；(2)中间虚线部分也是长方形,长是宽的1.6倍,用来设计；(3)四周空白部分的宽度相等.|
|信息2|如图(2),为了美观,将设计部分分割成大小相等的左中右三个长方形栏目,每个栏目书写8个字,栏目与栏目之间的中缝间距相等.|
|信息3|如图(3),每个栏目划出正方形方格,中间有十字间隔,竖向两列中间间隔(如CD)和横向中间间隔(如EF)宽度比为1∶2.|
|问题解决|
|任务1|设四周宽度为x cm,用含x的代数式分别表示设计部分的长和宽.|
|任务2|求四周宽度x的值.|
|任务3|(1)求每个栏目的水平宽度(如AB)；(2)求长方形栏目与栏目之间中缝的间距.|
答案：任务1:根据题意,得设计部分的长为(414 - 2x)cm,宽为(270 - 2x)cm.任务2:根据题意,得414 - 2x = 1.6(270 - 2x),解得x = 15.故四周宽度x的值为15.任务3:
(1)设CD = ycm,则EF = 2ycm,正方形方格的边长为$\frac{1}{4}(270 - 2×15 - 2y)=(60 - \frac{1}{2}y)cm$,
∴AB =$2(60 - \frac{1}{2}y)+y = 120 - y + y = 120(cm)$.故每个栏目的水平宽度为120cm.
(2)根据题意,得$\frac{414 - 2×15 - 120×3}{2}=12(cm)$.故长方形栏目与栏目之间中缝的间距为12cm.
(1)设CD = ycm,则EF = 2ycm,正方形方格的边长为$\frac{1}{4}(270 - 2×15 - 2y)=(60 - \frac{1}{2}y)cm$,
∴AB =$2(60 - \frac{1}{2}y)+y = 120 - y + y = 120(cm)$.故每个栏目的水平宽度为120cm.
(2)根据题意,得$\frac{414 - 2×15 - 120×3}{2}=12(cm)$.故长方形栏目与栏目之间中缝的间距为12cm.
7. 分类讨论思想 如图,甲、乙两个长方体容器放置在同一水平桌面上,容器甲的底面积为$80 dm^2,$高为6 dm；容器乙的底面积为$40 dm^2,$高为9 dm.容器甲中盛满水,容器乙中没有水,容器乙的最下方装有一只处在关闭状态的水龙头.现从容器甲向容器乙匀速注水,每分钟注水$20 dm^3.$
(1)水龙头关闭时,容器甲中水位的高度每分钟下降
(2)当容器乙注满水时,求此时容器甲中水位的高度.
(1)水龙头关闭时,容器甲中水位的高度每分钟下降
$\frac{1}{4}$
dm,容器乙中水位的高度每分钟上升$\frac{1}{2}$
dm.(2)当容器乙注满水时,求此时容器甲中水位的高度.
当容器乙注满水时,此时容器甲中水位的高度是$\frac{80×6 - 40×9}{80}=\frac{3}{2}(dm)$.
(3)在容器乙注满水的同时,打开水龙头开始放水,水龙头每分钟放水$60 dm^3.$从容器甲开始注水起,经过多长时间,两个容器中水位的高度相差4 dm？①在容器乙未注满水时,设开始注水x分钟,容器甲中水位比容器乙中水位高4dm.根据题意,得$(6 - \frac{1}{4}x)-\frac{1}{2}x = 4$,解得$x = \frac{8}{3}$,
∴开始注水$\frac{8}{3}$分钟,容器甲中水位比容器乙中水位高4dm;②在容器乙未注满水时,设开始注水y分钟,容器乙中水位比容器甲中水位高4dm.根据题意,得$\frac{1}{2}y-(6 - \frac{1}{4}y)=4$,解得$y = \frac{40}{3}$,
∴开始注水$\frac{40}{3}$分钟,容器乙中水位比容器甲中水位高4dm;③容器乙注满水后,设开始注水z分钟,容器乙中水位比容器甲中水位高4dm.根据题意,得$9-\frac{60 - 20}{40}×(z - \frac{40×9}{20})-(6 - \frac{1}{4}z)=4$,解得$z = \frac{68}{3}$.
∴容器乙中注满水后,开始注水$\frac{68}{3}$分钟,容器乙中水位比容器甲中水位高4dm.综上所述,从容器甲开始注水起,经过$\frac{8}{3}$分钟或$\frac{40}{3}$分钟或$\frac{68}{3}$分钟,两个容器中水位的高度相差4dm.
∴开始注水$\frac{8}{3}$分钟,容器甲中水位比容器乙中水位高4dm;②在容器乙未注满水时,设开始注水y分钟,容器乙中水位比容器甲中水位高4dm.根据题意,得$\frac{1}{2}y-(6 - \frac{1}{4}y)=4$,解得$y = \frac{40}{3}$,
∴开始注水$\frac{40}{3}$分钟,容器乙中水位比容器甲中水位高4dm;③容器乙注满水后,设开始注水z分钟,容器乙中水位比容器甲中水位高4dm.根据题意,得$9-\frac{60 - 20}{40}×(z - \frac{40×9}{20})-(6 - \frac{1}{4}z)=4$,解得$z = \frac{68}{3}$.
∴容器乙中注满水后,开始注水$\frac{68}{3}$分钟,容器乙中水位比容器甲中水位高4dm.综上所述,从容器甲开始注水起,经过$\frac{8}{3}$分钟或$\frac{40}{3}$分钟或$\frac{68}{3}$分钟,两个容器中水位的高度相差4dm.
答案：
(1)$\frac{1}{4}$ $\frac{1}{2}$ [解析]容器甲中水位的高度每分钟下降$\frac{20}{80}=\frac{1}{4}(dm)$,容器乙中水位的高度每分钟上升$\frac{20}{40}=\frac{1}{2}(dm)$.
(2)当容器乙注满水时,此时容器甲中水位的高度是$\frac{80×6 - 40×9}{80}=\frac{3}{2}(dm)$.
(3)①在容器乙未注满水时,设开始注水x分钟,容器甲中水位比容器乙中水位高4dm.根据题意,得$(6 - \frac{1}{4}x)-\frac{1}{2}x = 4$,解得$x = \frac{8}{3}$,
∴开始注水$\frac{8}{3}$分钟,容器甲中水位比容器乙中水位高4dm;②在容器乙未注满水时,设开始注水y分钟,容器乙中水位比容器甲中水位高4dm.根据题意,得$\frac{1}{2}y-(6 - \frac{1}{4}y)=4$,解得$y = \frac{40}{3}$,
∴开始注水$\frac{40}{3}$分钟,容器乙中水位比容器甲中水位高4dm;③容器乙注满水后,设开始注水z分钟,容器乙中水位比容器甲中水位高4dm.根据题意,得$9-\frac{60 - 20}{40}×(z - \frac{40×9}{20})-(6 - \frac{1}{4}z)=4$,解得$z = \frac{68}{3}$.
∴容器乙中注满水后,开始注水$\frac{68}{3}$分钟,容器乙中水位比容器甲中水位高4dm.综上所述,从容器甲开始注水起,经过$\frac{8}{3}$分钟或$\frac{40}{3}$分钟或$\frac{68}{3}$分钟,两个容器中水位的高度相差4dm.
(1)$\frac{1}{4}$ $\frac{1}{2}$ [解析]容器甲中水位的高度每分钟下降$\frac{20}{80}=\frac{1}{4}(dm)$,容器乙中水位的高度每分钟上升$\frac{20}{40}=\frac{1}{2}(dm)$.
(2)当容器乙注满水时,此时容器甲中水位的高度是$\frac{80×6 - 40×9}{80}=\frac{3}{2}(dm)$.
(3)①在容器乙未注满水时,设开始注水x分钟,容器甲中水位比容器乙中水位高4dm.根据题意,得$(6 - \frac{1}{4}x)-\frac{1}{2}x = 4$,解得$x = \frac{8}{3}$,
∴开始注水$\frac{8}{3}$分钟,容器甲中水位比容器乙中水位高4dm;②在容器乙未注满水时,设开始注水y分钟,容器乙中水位比容器甲中水位高4dm.根据题意,得$\frac{1}{2}y-(6 - \frac{1}{4}y)=4$,解得$y = \frac{40}{3}$,
∴开始注水$\frac{40}{3}$分钟,容器乙中水位比容器甲中水位高4dm;③容器乙注满水后,设开始注水z分钟,容器乙中水位比容器甲中水位高4dm.根据题意,得$9-\frac{60 - 20}{40}×(z - \frac{40×9}{20})-(6 - \frac{1}{4}z)=4$,解得$z = \frac{68}{3}$.
∴容器乙中注满水后,开始注水$\frac{68}{3}$分钟,容器乙中水位比容器甲中水位高4dm.综上所述,从容器甲开始注水起,经过$\frac{8}{3}$分钟或$\frac{40}{3}$分钟或$\frac{68}{3}$分钟,两个容器中水位的高度相差4dm.
8. 传统文化 幻方 (2024·攀枝花中考)幻方,中国古代称为“河图”“洛书”,又叫“纵横图”.如图所示的幻方中,每一行、每一列及各条对角线上的三个数之和均相等,则a的值为 .
答案：
3 [解析]如图: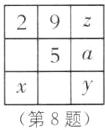
根据题意,得x + 5 + z = 2 + 9 + z,
∴x = 6.
∵9 + 5 = x + y,
∴y = 14 - 6 = 8.
∵a + y = 2 + 9,
∴a = 11 - 8 = 3.
3 [解析]如图:
根据题意,得x + 5 + z = 2 + 9 + z,∴x = 6.
∵9 + 5 = x + y,
∴y = 14 - 6 = 8.
∵a + y = 2 + 9,
∴a = 11 - 8 = 3.