26. 中考新考法 类比猜想 如图(1),△ABE 是等腰三角形,AB= AE,$∠BAE= 45^\circ,$过点 B 作 BC⊥AE 于点 C,在 BC 上截取 CD= CE,连接 AD,DE,并延长 AD 交 BE 于点 P.
(1)求证:AD= BE;
(2)试说明 AD 平分∠BAE;
(3)如图(2),将△CDE 绕着点 C 旋转一定的角度,那么 AD 与 BE 的位置关系是否发生变化,说明理由.
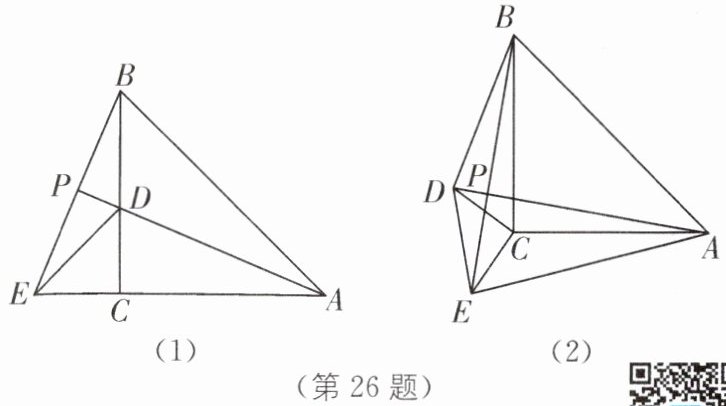
(1)求证:AD= BE;
(2)试说明 AD 平分∠BAE;
(3)如图(2),将△CDE 绕着点 C 旋转一定的角度,那么 AD 与 BE 的位置关系是否发生变化,说明理由.

答案:
(1)
∵BC⊥AE,∠BAE = 45°,
∴∠CBA = ∠CAB,
∴BC = AC.
在△BCE 和△ACD 中,{BC = AC,∠BCE = ∠ACD = 90°,CE = CD},
∴△BCE≌△ACD(SAS),
∴AD = BE.
(2)
∵△BCE≌△ACD,
∴∠EBC = ∠DAC.
∵∠BDP = ∠ADC,
∴∠BPD = ∠DCA = 90°.
∵AB = AE,
∴AD 平分∠BAE.
(3)AD 与 BE 的位置关系不发生变化. 理由如下:
如图,设 AD,BC 交于点 F.
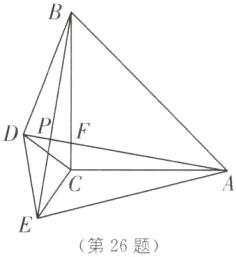
由
(1),得 BC = AC,∠BCA = ∠ECD = 90°,
∴∠BCA + ∠BCD = ∠ECD + ∠BCD,即∠ACD = ∠BCE.
又 CD = CE,
∴△BCE≌△ACD(SAS),
∴∠EBC = ∠DAC.
∵∠BFP = ∠AFC,
∴∠BPF = ∠ACF = 90°,
∴AD⊥BE.
(1)
∵BC⊥AE,∠BAE = 45°,
∴∠CBA = ∠CAB,
∴BC = AC.
在△BCE 和△ACD 中,{BC = AC,∠BCE = ∠ACD = 90°,CE = CD},
∴△BCE≌△ACD(SAS),
∴AD = BE.
(2)
∵△BCE≌△ACD,
∴∠EBC = ∠DAC.
∵∠BDP = ∠ADC,
∴∠BPD = ∠DCA = 90°.
∵AB = AE,
∴AD 平分∠BAE.
(3)AD 与 BE 的位置关系不发生变化. 理由如下:
如图,设 AD,BC 交于点 F.

由
(1),得 BC = AC,∠BCA = ∠ECD = 90°,
∴∠BCA + ∠BCD = ∠ECD + ∠BCD,即∠ACD = ∠BCE.
又 CD = CE,
∴△BCE≌△ACD(SAS),
∴∠EBC = ∠DAC.
∵∠BFP = ∠AFC,
∴∠BPF = ∠ACF = 90°,
∴AD⊥BE.
27. 用两个全等的等边三角形 ABC 和△ACD 拼成四边形 ABCD,把一个含$ 60^\circ $角的三角尺与这个四边形叠合,使三角尺的$ 60^\circ $角的顶点与点 A 重合,两边分别与 AB,AC 重合,将三角尺绕点 A 按逆时针方向旋转.
(1)当三角尺的两边分别与四边形的两边 BC,CD 相交于点 E,F 时(如图(1)),通过比较 BE,CF 的长度,你能得出什么结论?并说明理由.
(2)当三角尺的两边分别与四边形的两边 BC,CD 的延长线相交于点 E,F 时(如图(2)),你在(1)中得到的结论还成立吗?简要说明理由.

(1)当三角尺的两边分别与四边形的两边 BC,CD 相交于点 E,F 时(如图(1)),通过比较 BE,CF 的长度,你能得出什么结论?并说明理由.
(2)当三角尺的两边分别与四边形的两边 BC,CD 的延长线相交于点 E,F 时(如图(2)),你在(1)中得到的结论还成立吗?简要说明理由.

答案:
(1)BE = CF. 理由如下:
∵△ABC 和△ACD 都是等边三角形,
∴∠BAC = ∠B = ∠ACD = 60°,AB = AC.
∵∠EAF = ∠BAC = 60°,
∴∠CAF + ∠CAE = ∠CAE + ∠BAE,
∴∠CAF = ∠BAE.
在△ABE 和△ACF 中,{∠B = ∠ACF,AB = AC,∠BAE = ∠CAF},
∴△ABE≌△ACF(ASA),
∴BE = CF.
(2)成立. 理由如下:
∵△ABC 和△ACD 都是等边三角形,
∴∠ACB = ∠ADC = ∠CAD = 60°,AC = AD = BC = CD,
∴∠ACE = ∠ADF = 120°.
∵∠EAF = ∠CAD = 60°,
∴∠EAF - ∠EAD = ∠CAD - ∠EAD,
∴∠CAE = ∠DAF.
在△ACE 和△ADF 中,{∠CAE = ∠DAF,AC = AD,∠ACE = ∠ADF},
∴△ACE≌△ADF(ASA),
∴CE = DF,
∴CE + BC = DF + CD,即 BE = CF.
归纳总结:三角形全等的判定是中考的热点,一般以考查三角形全等的判定方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.
(1)BE = CF. 理由如下:
∵△ABC 和△ACD 都是等边三角形,
∴∠BAC = ∠B = ∠ACD = 60°,AB = AC.
∵∠EAF = ∠BAC = 60°,
∴∠CAF + ∠CAE = ∠CAE + ∠BAE,
∴∠CAF = ∠BAE.
在△ABE 和△ACF 中,{∠B = ∠ACF,AB = AC,∠BAE = ∠CAF},
∴△ABE≌△ACF(ASA),
∴BE = CF.
(2)成立. 理由如下:
∵△ABC 和△ACD 都是等边三角形,
∴∠ACB = ∠ADC = ∠CAD = 60°,AC = AD = BC = CD,
∴∠ACE = ∠ADF = 120°.
∵∠EAF = ∠CAD = 60°,
∴∠EAF - ∠EAD = ∠CAD - ∠EAD,
∴∠CAE = ∠DAF.
在△ACE 和△ADF 中,{∠CAE = ∠DAF,AC = AD,∠ACE = ∠ADF},
∴△ACE≌△ADF(ASA),
∴CE = DF,
∴CE + BC = DF + CD,即 BE = CF.
归纳总结:三角形全等的判定是中考的热点,一般以考查三角形全等的判定方法为主,判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.