23.(2024·苏州昆山一模)如图,在△ABC 中,D 为 AB 上一点,E 为 AC 中点,连接 DE 并延长至点 F,使得 EF= ED,连接 CF.
(1)求证:CF//AB;
(2)若$∠A= 70^\circ,$$∠F= 35^\circ,$BE⊥AC,求∠BED 的度数.
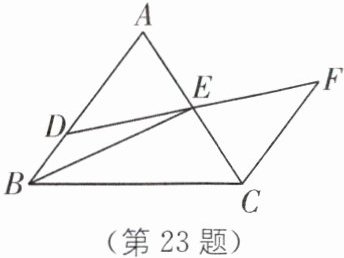
(1)求证:CF//AB;
(2)若$∠A= 70^\circ,$$∠F= 35^\circ,$BE⊥AC,求∠BED 的度数.

答案:
(1)
∵E 为 AC 中点,
∴AE = CE,
在△AED 和△CEF 中,{AE = CE,∠AED = ∠CEF,DE = EF},
∴△AED≌△CEF(SAS),
∴∠A = ∠ACF,
∴CF//AB.
(2)
∵∠A = ∠ACF = 70°,∠F = 35°,
∴∠AED = ∠CEF = 180° - 70° - 35° = 75°,
∵BE⊥AC,
∴∠AEB = 90°,
∴∠BED = 90° - 75° = 15°.
(1)
∵E 为 AC 中点,
∴AE = CE,
在△AED 和△CEF 中,{AE = CE,∠AED = ∠CEF,DE = EF},
∴△AED≌△CEF(SAS),
∴∠A = ∠ACF,
∴CF//AB.
(2)
∵∠A = ∠ACF = 70°,∠F = 35°,
∴∠AED = ∠CEF = 180° - 70° - 35° = 75°,
∵BE⊥AC,
∴∠AEB = 90°,
∴∠BED = 90° - 75° = 15°.
24.(2024·泰州高港区期中)如图,ED⊥AB,FC⊥AB,垂足分别为 D,C,请从①AE//BF;②AE= BF;③AC= BD 中选择两个作为补充条件,余下一个作为结论,并写出结论成立的证明过程. 你选的补充条件是

①②
,结论是③
.(填序号)
答案:补充条件选①②,结论为③.(答案不唯一)证明如下:
∵AE//BF,
∴∠A = ∠B.
∵ED⊥AB,FC⊥AB,
∴∠ADE = ∠FCB = 90°.
在△ADE 与△BCF 中,{∠ADE = ∠BCF,∠A = ∠B,AE = BF},
∴△ADE≌△BCF(AAS),
∴AD = CB,
∴AC = BD.
或补充条件是①③,结论是②或补充条件是②③,结论是①,证明略.
∵AE//BF,
∴∠A = ∠B.
∵ED⊥AB,FC⊥AB,
∴∠ADE = ∠FCB = 90°.
在△ADE 与△BCF 中,{∠ADE = ∠BCF,∠A = ∠B,AE = BF},
∴△ADE≌△BCF(AAS),
∴AD = CB,
∴AC = BD.
或补充条件是①③,结论是②或补充条件是②③,结论是①,证明略.
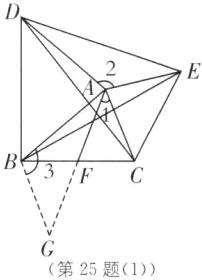
25.(2025·无锡锡山高级中学实验学校期中)如图,在△ABC 中,以 AB,AC 为边向外作等腰三角形 ABD,△ACE,且 AB= AD,AC= AE,F 为 BC 中点,∠DAB= ∠CAE= α. 连接 DE,DC,BE,AF.
(1)证明△ADC≌△ABE;
(2)当 DE= 2AF 时,
①求 α 的大小;
②判断△ABC 与△ADE 面积之间的关系,并说明理由.

(1)证明△ADC≌△ABE;
(2)当 DE= 2AF 时,
①求 α 的大小;
②判断△ABC 与△ADE 面积之间的关系,并说明理由.

答案:
(1)
∵∠DAB = ∠CAE = α,
∴∠DAB + ∠BAC = ∠CAE + ∠BAC,
即∠DAC = ∠EAB,
在△DAC 和△BAE 中,{AB = AD,∠DAC = ∠EAB,AC = AE},
∴△ADC≌△ABE(SAS).
(2)①如图
(1),延长 AF 至 G,使得 GF = AF,连接 BG.
∵F 为 BC 中点,
∴BF = CF = $\frac{1}{2}$BC.
在△GFB 和△AFC 中,{GF = AF,∠BFG = ∠AFC,BF = CF},
∴△GFB≌△AFC(SAS),
∴AC = BG,∠1 = ∠G.
∵DE = 2AF,
∴DE = AG.
∵AB = AD,AC = AE,
∴BG = AE,
在△ABG 和△DAE 中,{AG = DE,AB = AD,BG = AE},
∴△ABG≌△DAE(SSS),
∴∠2 = ∠3.
∵∠3 + ∠BAG + ∠G = 180°,
∴∠2 + ∠BAG + ∠1 = 180°,
即∠DAB + ∠EAC = 360° - (∠2 + ∠BAG + ∠1) = 180°,
∴2α = 180°,则 α = 90°.
②△ABC 与△ADE 面积相等. 理由如下:
如图
(2),过点 C 作 CM⊥AB 于点 M,过点 E 作 EN⊥DA 交 DA 延长线于 N,

∵α = 90°,
∴△ABD 和△ACE 都是等腰直角三角形.
∵∠BAD + ∠CAE + ∠BAC + ∠DAE = 360°,
∴∠BAC + ∠DAE = 180°.
∵∠DAE + ∠EAN = 180°,
∴∠BAC = ∠EAN,
在△ACM 和△AEN 中,{∠MAC = ∠NAE,∠AMC = ∠ANE,AC = AE},
∴△ACM≌△AEN(AAS),
∴CM = EN.
∵S△ABC = $\frac{1}{2}$AB·CM,S△ADE = $\frac{1}{2}$AD·EN,
∴S△ABC = S△ADE.
(1)
∵∠DAB = ∠CAE = α,
∴∠DAB + ∠BAC = ∠CAE + ∠BAC,
即∠DAC = ∠EAB,
在△DAC 和△BAE 中,{AB = AD,∠DAC = ∠EAB,AC = AE},
∴△ADC≌△ABE(SAS).
(2)①如图
(1),延长 AF 至 G,使得 GF = AF,连接 BG.

∵F 为 BC 中点,
∴BF = CF = $\frac{1}{2}$BC.
在△GFB 和△AFC 中,{GF = AF,∠BFG = ∠AFC,BF = CF},
∴△GFB≌△AFC(SAS),
∴AC = BG,∠1 = ∠G.
∵DE = 2AF,
∴DE = AG.
∵AB = AD,AC = AE,
∴BG = AE,
在△ABG 和△DAE 中,{AG = DE,AB = AD,BG = AE},
∴△ABG≌△DAE(SSS),
∴∠2 = ∠3.
∵∠3 + ∠BAG + ∠G = 180°,
∴∠2 + ∠BAG + ∠1 = 180°,
即∠DAB + ∠EAC = 360° - (∠2 + ∠BAG + ∠1) = 180°,
∴2α = 180°,则 α = 90°.
②△ABC 与△ADE 面积相等. 理由如下:
如图
(2),过点 C 作 CM⊥AB 于点 M,过点 E 作 EN⊥DA 交 DA 延长线于 N,

∵α = 90°,
∴△ABD 和△ACE 都是等腰直角三角形.
∵∠BAD + ∠CAE + ∠BAC + ∠DAE = 360°,
∴∠BAC + ∠DAE = 180°.
∵∠DAE + ∠EAN = 180°,
∴∠BAC = ∠EAN,
在△ACM 和△AEN 中,{∠MAC = ∠NAE,∠AMC = ∠ANE,AC = AE},
∴△ACM≌△AEN(AAS),
∴CM = EN.
∵S△ABC = $\frac{1}{2}$AB·CM,S△ADE = $\frac{1}{2}$AD·EN,
∴S△ABC = S△ADE.