11.(2025·连云港期中)如图,在△ABC 中,$∠ACB= 90^\circ,$$∠A= 52^\circ,$将其折叠,使点 A 落在边 BC 上的点 E 处,CA 与 CE 重合,折痕为 CD,则∠EDB 的度数是______.


14°
答案:14° [解析]在△ABC 中,∠ACB = 90°,∠A = 52°,
∴∠B = 90° - 52° = 38°,
由题意,可知△ECD≌△ACD,
∴∠CED = ∠A = 52°,
由图可知,∠CED 是△EBD 的外角,
∴∠CED = ∠B + ∠EDB,
∴52° = 38° + ∠EDB,
∴∠EDB = 14°.
∴∠B = 90° - 52° = 38°,
由题意,可知△ECD≌△ACD,
∴∠CED = ∠A = 52°,
由图可知,∠CED 是△EBD 的外角,
∴∠CED = ∠B + ∠EDB,
∴52° = 38° + ∠EDB,
∴∠EDB = 14°.
12.(2024·牡丹江中考)如图,在△ABC 中,D 是 AB 上一点,CF//AB,D,E,F 三点共线,请添加一个条件______
DE = EF
,使得 AE= CE.(只需填一种情况即可)答案:DE = EF 或 AD = CF(答案不唯一) [解析]
∵CF//AB,
∴∠A = ∠ECF,∠ADE = ∠CFE,
∴添加条件 DE = EF,可以使得△ADE≌△CFE(AAS),添加条件 AD = CF,可以使得△ADE≌△CFE(ASA).
∵CF//AB,
∴∠A = ∠ECF,∠ADE = ∠CFE,
∴添加条件 DE = EF,可以使得△ADE≌△CFE(AAS),添加条件 AD = CF,可以使得△ADE≌△CFE(ASA).
13. 如图,D,C 为 AF 上两点,AD= CF,∠A= ∠EDF,要用 ASA 判定△ABC≌△DEF,需补充角的条件是
∠ACB = ∠F
.答案:∠ACB = ∠F [解析]
∵AD = CF,
∴AC = DF.
∵∠A = ∠EDF,
∴要用 ASA 判定△ABC≌△DEF,需补充角的条件是∠ACB = ∠F.
∵AD = CF,
∴AC = DF.
∵∠A = ∠EDF,
∴要用 ASA 判定△ABC≌△DEF,需补充角的条件是∠ACB = ∠F.
14. 如图,在△ABC 和△ADC 中,AB= AD,AC 平分∠DAB,$∠B= 120^\circ,$$∠DAB= 66^\circ,$则∠DCA 的度数是
27°
.答案:27° [解析]
∵AC 平分∠DAB,∠DAB = 66°,
∴∠DAC = ∠BAC = 33°.
在△ADC 和△ABC 中,{AD = AB,∠DAC = ∠BAC,AC = AC},
∴△ADC≌△ABC(SAS),
∴∠ACD = ∠ACB.
∵∠B = 120°,
∴∠DCA = ∠ACB = 180° - 120° - 33° = 27°.
∵AC 平分∠DAB,∠DAB = 66°,
∴∠DAC = ∠BAC = 33°.
在△ADC 和△ABC 中,{AD = AB,∠DAC = ∠BAC,AC = AC},
∴△ADC≌△ABC(SAS),
∴∠ACD = ∠ACB.
∵∠B = 120°,
∴∠DCA = ∠ACB = 180° - 120° - 33° = 27°.
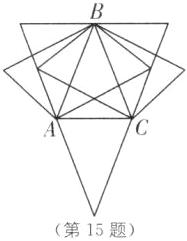
15. 在△ABC 中,已知 AB= BC≠AC,作与△ABC 只有一条公共边,且与△ABC 全等的三角形,这样的三角形一共能作出______个.
答案:
7 [解析]如图,以 AB 为公共边有三个,以 CB 为公共边有三个,以 AC 为公共边有一个,
所以一共能作出 7 个.
归纳总结:本题考查了全等三角形的作法. 作三角形时要根据全等三角形的判定方法的要求,正确对每种情况进行讨论是解决本题的关键.
7 [解析]如图,以 AB 为公共边有三个,以 CB 为公共边有三个,以 AC 为公共边有一个,

所以一共能作出 7 个.
归纳总结:本题考查了全等三角形的作法. 作三角形时要根据全等三角形的判定方法的要求,正确对每种情况进行讨论是解决本题的关键.
16. 中考新考法 满足结论的条件开放 如图,点 A 和动点 P 在直线 l 上,点 P 关于点 A 的对称点为 Q,以 AQ 为边作 Rt△ABQ,使$∠BAQ= 90^\circ,$AQ:AB= 3:4. 直线 l 上有一点 C 在点 P 右侧,PC= 4 cm,过点 C 作射线 CD⊥l,点 F 为射线 CD 上的一个动点,连接 AF. 当△AFC 与△ABQ 全等时,AQ=
12 或 2 或 $\frac{12}{7}$
cm.答案:12 或 2 或 $\frac{12}{7}$ [解析]当点 P 在点 A 的右侧时,AC 不可能等于 AQ,要使三角形全等,只能 AC = AB.
要使△AFC 与△ABQ 全等,则应满足{AB = CA,∠BAQ = ∠ACF,AQ = CF}.
∵AQ:AB = 3:4,AQ = AP,PC = 4cm,
∴设 AQ = 3xcm,AB = 4xcm,则有 4x - 3x = 4,
∴x = 4,
∴AQ = 12cm.
当点 P 在点 A 的左侧时,若 AC = AQ(即 C,Q 重合),可得 AQ = 2cm;
若 AC = AB,可得 AQ = $\frac{12}{7}$cm.
故当△AFC 与△ABQ 全等时,AQ = 12cm 或 2cm 或 $\frac{12}{7}$cm.
要使△AFC 与△ABQ 全等,则应满足{AB = CA,∠BAQ = ∠ACF,AQ = CF}.
∵AQ:AB = 3:4,AQ = AP,PC = 4cm,
∴设 AQ = 3xcm,AB = 4xcm,则有 4x - 3x = 4,
∴x = 4,
∴AQ = 12cm.
当点 P 在点 A 的左侧时,若 AC = AQ(即 C,Q 重合),可得 AQ = 2cm;
若 AC = AB,可得 AQ = $\frac{12}{7}$cm.
故当△AFC 与△ABQ 全等时,AQ = 12cm 或 2cm 或 $\frac{12}{7}$cm.
17.(2024·南京联合体期中)在△ABC 中,$∠A= 30^\circ,$AB= 2. 若对于 BC 的每一个值,对应的△ABC 的形状、大小都唯一确定,则 BC 长的取值范围是
BC = 1 或 BC≥2
.答案:BC = 1 或 BC≥2 [解析]当 BC⊥AC 时,由“HL”判定△ABC 的形状、大小都唯一确定.
∵∠A = 30°,
∴BC = $\frac{1}{2}$AB = $\frac{1}{2}$×2 = 1.
以 B 为圆心,大于或等于 AB 的长为半径画弧,与射线 BC 只有一个交点(A 除外),此时△ABC 的形状、大小都唯一确定,
∴BC≥2,
∴BC 长的取值范围是 BC = 1 或 BC≥2.
∵∠A = 30°,
∴BC = $\frac{1}{2}$AB = $\frac{1}{2}$×2 = 1.
以 B 为圆心,大于或等于 AB 的长为半径画弧,与射线 BC 只有一个交点(A 除外),此时△ABC 的形状、大小都唯一确定,
∴BC≥2,
∴BC 长的取值范围是 BC = 1 或 BC≥2.
18. 如图,在△ABC 中,$∠A= 90^\circ,$AB= AC,∠ABC 的平分线 BD 交 AC 于点 D,CE⊥BD,交 BD 的延长线于点 E,若 BD= 7,则 CE= ______.


答案:
3.5 [解析]如图,延长 BA,CE 相交于点 F.

∵BD 平分∠ABC,
∴∠ABD = ∠CBD.
在△BCE 和△BFE 中,{∠CBE = ∠FBE,BE = BE,∠BEC = ∠BEF = 90°},
∴△BCE≌△BFE(ASA),
∴EC = EF.
∵∠BAC = 90°,CE⊥BD,
∴∠ACF + ∠F = 90°,∠ABD + ∠F = 90°,
∴∠ABD = ∠ACF.
在△ABD 和△ACF 中,{∠ABD = ∠ACF,AB = AC,∠BAD = ∠CAF = 90°},
∴△ABD≌△ACF(ASA),
∴BD = CF.
∵CF = CE + EF = 2CE,
∴BD = 2CE = 7,
∴CE = 3.5.
3.5 [解析]如图,延长 BA,CE 相交于点 F.

∵BD 平分∠ABC,
∴∠ABD = ∠CBD.
在△BCE 和△BFE 中,{∠CBE = ∠FBE,BE = BE,∠BEC = ∠BEF = 90°},
∴△BCE≌△BFE(ASA),
∴EC = EF.
∵∠BAC = 90°,CE⊥BD,
∴∠ACF + ∠F = 90°,∠ABD + ∠F = 90°,
∴∠ABD = ∠ACF.
在△ABD 和△ACF 中,{∠ABD = ∠ACF,AB = AC,∠BAD = ∠CAF = 90°},
∴△ABD≌△ACF(ASA),
∴BD = CF.
∵CF = CE + EF = 2CE,
∴BD = 2CE = 7,
∴CE = 3.5.
19.(2025·无锡江阴期中)如图,四边形 ABCD 中,AC= BC,$∠ACB= ∠ADC= 90^\circ,$CD= 8,则△BCD 的面积为______.


答案:
32 [解析]如图,过点 B 作 BH⊥DC 交 DC 的延长线于点 H.

∵∠H = ∠ACB = ∠ADC = 90°,
∴∠BCH + ∠ACD = 90°,∠ACD + ∠CAD = 90°,
∴∠BCH = ∠CAD,
在△BHC 和△CDA 中,{∠H = ∠ADC,∠BCH = ∠CAD,CB = AC},
∴△BHC≌△CDA(AAS),
∴BH = CD = 8,
∴S△BCD = $\frac{1}{2}$CD·BH = $\frac{1}{2}$×8×8 = 32.
32 [解析]如图,过点 B 作 BH⊥DC 交 DC 的延长线于点 H.

∵∠H = ∠ACB = ∠ADC = 90°,
∴∠BCH + ∠ACD = 90°,∠ACD + ∠CAD = 90°,
∴∠BCH = ∠CAD,
在△BHC 和△CDA 中,{∠H = ∠ADC,∠BCH = ∠CAD,CB = AC},
∴△BHC≌△CDA(AAS),
∴BH = CD = 8,
∴S△BCD = $\frac{1}{2}$CD·BH = $\frac{1}{2}$×8×8 = 32.
20.(2025·南京中华中学初中部期中)在△ABC 中,AC= 5,中线 AD= 4,则边 AB 的取值范围是______.
答案:
3<AB<13 [解析]如图,延长 AD 至点 E,使 DE = AD,连接 CE.

∵AD 是△ABC 的中线,
∴BD = CD.
在△ABD 和△ECD 中,{BD = CD,∠ADB = ∠EDC,AD = DE},
∴△ABD≌△ECD(SAS),
∴AB = EC.
∵AD = 4,
∴AE = 4 + 4 = 8.
∵8 + 5 = 13,8 - 5 = 3,
∴3<EC<13,
即 3<AB<13.
方法诠释:本题主要考查了全等三角形的判定与性质和三角形的三边关系,在三角形中任意两边之和大于第三边,任意两边之差小于第三边,“遇中线,加倍延”构造出全等三角形是解题的关键.
3<AB<13 [解析]如图,延长 AD 至点 E,使 DE = AD,连接 CE.

∵AD 是△ABC 的中线,
∴BD = CD.
在△ABD 和△ECD 中,{BD = CD,∠ADB = ∠EDC,AD = DE},
∴△ABD≌△ECD(SAS),
∴AB = EC.
∵AD = 4,
∴AE = 4 + 4 = 8.
∵8 + 5 = 13,8 - 5 = 3,
∴3<EC<13,
即 3<AB<13.
方法诠释:本题主要考查了全等三角形的判定与性质和三角形的三边关系,在三角形中任意两边之和大于第三边,任意两边之差小于第三边,“遇中线,加倍延”构造出全等三角形是解题的关键.
21. 如图,△ABC 的顶点都在小正方形的顶点上,试在网格纸上按下列要求画格点三角形.
(1)画一个三角形与△ABC 全等且只有一个公共点;
(2)画一个三角形与△ABC 全等且只有一条公共边.

(1)画一个三角形与△ABC 全等且只有一个公共点;
(2)画一个三角形与△ABC 全等且只有一条公共边.

答案:
(1)如图,△A₁BC 即为所求.(答案不唯一)

(2)如图,△ABC₂ 即为所求.(答案不唯一)
(1)如图,△A₁BC 即为所求.(答案不唯一)

(2)如图,△ABC₂ 即为所求.(答案不唯一)
22.(2024·南通一模)如图,已知 A,D,C,E 在同一直线上,BC 和 DF 相交于点 O,AD= CE,AB//DF,AB= DF.
(1)求证:△ABC≌△DFE;
(2)连接 CF,若$∠BCF= 54^\circ,$$∠DFC= 20^\circ,$求∠DFE 的度数.

(1)求证:△ABC≌△DFE;
(2)连接 CF,若$∠BCF= 54^\circ,$$∠DFC= 20^\circ,$求∠DFE 的度数.

答案:
(1)
∵AB//DF,
∴∠A = ∠EDF.
∵AD = CE,
∴AD + CD = CE + CD,即 AC = DE.
在△ABC 和△DFE 中,{AB = DF,∠A = ∠FDE,AC = DE},
∴△ABC≌△DFE(SAS).
(2)
∵∠BCF = 54°,∠DFC = 20°,
∴∠DOC = ∠BCF + ∠DFC = 54° + 20° = 74°.
∵AB//DF,
∴∠B = ∠DOC = 74°.
∵△ABC≌△DFE,
∴∠DFE = ∠B = 74°.
(1)
∵AB//DF,
∴∠A = ∠EDF.
∵AD = CE,
∴AD + CD = CE + CD,即 AC = DE.
在△ABC 和△DFE 中,{AB = DF,∠A = ∠FDE,AC = DE},
∴△ABC≌△DFE(SAS).
(2)
∵∠BCF = 54°,∠DFC = 20°,
∴∠DOC = ∠BCF + ∠DFC = 54° + 20° = 74°.
∵AB//DF,
∴∠B = ∠DOC = 74°.
∵△ABC≌△DFE,
∴∠DFE = ∠B = 74°.