1.(2025·广东广州天河期末)如图,CE 是△ADC 的边 AD 上的高. 若$∠BAD= 40^\circ,$$∠ECD= 25^\circ,$则∠B 的度数为$(
B
).A. 20^\circB. 25^\circC. 30^\circD. 35^\circ$答案:B [解析]
∵CE 是△ADC 边 AD 上的高,∠BAD = 40°,
∴∠CED = 90°.
∵∠ECD = 25°,
∴∠EDC = 90° - 25° = 65°,
∴∠B = ∠EDC - ∠BAD = 65° - 40° = 25°. 故选 B.
∵CE 是△ADC 边 AD 上的高,∠BAD = 40°,
∴∠CED = 90°.
∵∠ECD = 25°,
∴∠EDC = 90° - 25° = 65°,
∴∠B = ∠EDC - ∠BAD = 65° - 40° = 25°. 故选 B.
2.(2025·南通海安期末)如图,将△ABC 绕 B 点顺时针方向旋转到△DBE,点 A 的对应点 D 恰好落在 AC 上,且 BE//AC. 若$∠A= 70^\circ,$则∠C 的度数为$( )$
B
.A. 30°B. 40°C. 45°D. 36°答案:B [解析]由旋转,可得 DB = AB,
∴∠ADB = ∠A = 70°,∠ABC = ∠DBE,
∵点 D 在 AC 上,且 BE//AC,
∴∠DBE = ∠ADB = 70°,
∴∠ABC = ∠DBE = 70°,
∴∠C = 180° - ∠A - ∠ABC = 180° - 70° - 70° = 40°.
故选 B.
归纳总结:本题考查了旋转的性质,在旋转过程中根据旋转的性质确定相等的角和相等的线段是解题的关键.
∴∠ADB = ∠A = 70°,∠ABC = ∠DBE,
∵点 D 在 AC 上,且 BE//AC,
∴∠DBE = ∠ADB = 70°,
∴∠ABC = ∠DBE = 70°,
∴∠C = 180° - ∠A - ∠ABC = 180° - 70° - 70° = 40°.
故选 B.
归纳总结:本题考查了旋转的性质,在旋转过程中根据旋转的性质确定相等的角和相等的线段是解题的关键.
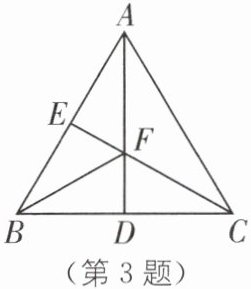
3. 如图,在△ABC 中,AB= BC,AD,CE 分别是边 BC,AB 上的中线,交于点 F,则图中有全等三角形(
A.2 对
B.3 对
C.4 对
D.5 对
D
).
A.2 对
B.3 对
C.4 对
D.5 对
答案:D [解析]
∵AB = BC,AD,CE 分别是边 BC,AB 上的中线,
∴BD = BE = AE = CD.
∵∠ABD = ∠CBE,
∴△ABD≌△CBE(SAS),
∴∠BAD = ∠BCE.
∵∠AFE = ∠CFD,
∴△AEF≌△CDF(AAS),
∴EF = DF,AF = CF,
∴EC = AD,
∴△BEF≌△BDF(SSS),△ABF≌△CBF(SSS),△AEC≌△CDA(SSS). 故选 D.
∵AB = BC,AD,CE 分别是边 BC,AB 上的中线,
∴BD = BE = AE = CD.
∵∠ABD = ∠CBE,
∴△ABD≌△CBE(SAS),
∴∠BAD = ∠BCE.
∵∠AFE = ∠CFD,
∴△AEF≌△CDF(AAS),
∴EF = DF,AF = CF,
∴EC = AD,
∴△BEF≌△BDF(SSS),△ABF≌△CBF(SSS),△AEC≌△CDA(SSS). 故选 D.
4.(2025·扬州江都区期末)根据下列条件,不能画出唯一确定的△ABC 的是(
A.AB= 3,BC= 4,AC= 6
$B.AB= 4,∠B= 45^\circ,∠A= 60^\circ$
C.AB= 4,$BC= 3,$∠A= 30^\circ
$D.∠C= 90^\circ,AB= 8,AC= 4$
C
).A.AB= 3,BC= 4,AC= 6
$B.AB= 4,∠B= 45^\circ,∠A= 60^\circ$
C.AB= 4,$BC= 3,$∠A= 30^\circ
$D.∠C= 90^\circ,AB= 8,AC= 4$
答案:C [解析]A. 三边确定,符合全等三角形判定定理 SSS,能画出唯一的△ABC. 故不符合题意;
B. 已知两个角及其公共边,符合全等三角形判定定理 ASA,能画出唯一的△ABC. 故不符合题意;
C. 已知两边及其中一边的对角,属于“SSA”的情况,不符合全等三角形判定定理. 故不能画出唯一的三角形. 故本选项符合题意;
D. 已知一个直角和一条直角边以及斜边长,符合全等三角形判定定理 HL,能画出唯一的△ABC. 故不符合题意. 故选 C.
B. 已知两个角及其公共边,符合全等三角形判定定理 ASA,能画出唯一的△ABC. 故不符合题意;
C. 已知两边及其中一边的对角,属于“SSA”的情况,不符合全等三角形判定定理. 故不能画出唯一的三角形. 故本选项符合题意;
D. 已知一个直角和一条直角边以及斜边长,符合全等三角形判定定理 HL,能画出唯一的△ABC. 故不符合题意. 故选 C.
5.(2025·连云港海州区期中)如图,已知 OC 平分∠AOB,CD//OB,若 OD= 4,则 CD 的长为(
A.4
B.5
C.3
D.2
A
).A.4
B.5
C.3
D.2
答案:A [解析]
∵OC 平分∠AOB,
∴∠DOC = ∠BOC.
∵CD//OB,
∴根据平行线的性质,得∠DCO = ∠BOC,
∴∠DCO = ∠DOC,
∴根据等腰三角形的性质,CD = OD = 4. 故选 A.
∵OC 平分∠AOB,
∴∠DOC = ∠BOC.
∵CD//OB,
∴根据平行线的性质,得∠DCO = ∠BOC,
∴∠DCO = ∠DOC,
∴根据等腰三角形的性质,CD = OD = 4. 故选 A.
6. 如图,在△ABC 中,AB= AC,D 为 BC 上一点,BF= CD,CE= BD,那么∠EDF 等于

B
$.A. 90^\circ-\angle AB. 90^\circ-\frac{1}{2}\angle AC. 180^\circ-\angle AD. 45^\circ-\frac{1}{2}\angle A$
答案:B [解析]
∵AB = AC,
∴∠B = ∠C.
在△BDF 和△CED 中,{BF = CD,∠B = ∠C,BD = CE},
∴△BDF≌△CED(SAS),
∴∠BFD = ∠CDE,
∴∠FDB + ∠EDC = ∠FDB + ∠BFD = 180° - ∠B = 180° - $\frac{180° - ∠A}{2}$ = 90° + $\frac{1}{2}$∠A,
则∠EDF = 180° - (∠FDB + ∠EDC) = 90° - $\frac{1}{2}$∠A. 故选 B.
∵AB = AC,
∴∠B = ∠C.
在△BDF 和△CED 中,{BF = CD,∠B = ∠C,BD = CE},
∴△BDF≌△CED(SAS),
∴∠BFD = ∠CDE,
∴∠FDB + ∠EDC = ∠FDB + ∠BFD = 180° - ∠B = 180° - $\frac{180° - ∠A}{2}$ = 90° + $\frac{1}{2}$∠A,
则∠EDF = 180° - (∠FDB + ∠EDC) = 90° - $\frac{1}{2}$∠A. 故选 B.
7. 如图,在△ABC 和△DEF 中,给出以下 6 个条件中,以其中 3 个作为已知条件,不能判断△ABC 和△DEF 全等的是(
①AB= DE;②BC= EF;③AC= DF;④∠A= ∠D;⑤∠B= ∠E;⑥∠C= ∠F.

A.①②⑤
B.①②③
C.①④⑥
D.②③④
D
).①AB= DE;②BC= EF;③AC= DF;④∠A= ∠D;⑤∠B= ∠E;⑥∠C= ∠F.

A.①②⑤
B.①②③
C.①④⑥
D.②③④
答案:D [解析]在△ABC 和△DEF 中,{AB = DE,∠B = ∠E,BC = EF},
∴△ABC≌△DEF(SAS). 故选项 A 不符合题意;
在△ABC 和△DEF 中,{AB = DE,BC = EF,AC = DF},
∴△ABC≌△DEF(SSS). 故选项 B 不符合题意;
在△ABC 和△DEF 中,{∠C = ∠F,∠A = ∠D,AB = DE},
∴△ABC≌△DEF(AAS). 故选项 C 不符合题意;
在△ABC 和△DEF 中,BC = EF,AC = DF,∠A = ∠D,不能判断△ABC 和△DEF 全等. 故选 D.
易错警示:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS,SAS,ASA,AAS,HL. 其中 AAA,SSA 不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与. 若有两边一角对应相等时,角必须是两边的夹角.
∴△ABC≌△DEF(SAS). 故选项 A 不符合题意;
在△ABC 和△DEF 中,{AB = DE,BC = EF,AC = DF},
∴△ABC≌△DEF(SSS). 故选项 B 不符合题意;
在△ABC 和△DEF 中,{∠C = ∠F,∠A = ∠D,AB = DE},
∴△ABC≌△DEF(AAS). 故选项 C 不符合题意;
在△ABC 和△DEF 中,BC = EF,AC = DF,∠A = ∠D,不能判断△ABC 和△DEF 全等. 故选 D.
易错警示:本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS,SAS,ASA,AAS,HL. 其中 AAA,SSA 不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与. 若有两边一角对应相等时,角必须是两边的夹角.
8.(2024·无锡梁溪区期中)如图,在△ABC 和△ADE 中,$∠CAB= ∠DAE= 36^\circ,$AB= AC,AD= AE. 连接 CD,连接 BE 并延长交 AC,AD 于点 F,G. 若 BE 恰好平分∠ABC,则下列结论错误的是(
A.∠ADC= ∠AEB
B.CD//AB
C.DE= GE
D.CD= BE
C
).A.∠ADC= ∠AEB
B.CD//AB
C.DE= GE
D.CD= BE
答案:C [解析]
∵∠CAB = ∠DAE = 36°,
∴∠CAB - ∠CAE = ∠DAE - ∠CAE,即∠DAC = ∠EAB.
在△DAC 和△EAB 中,{AD = AE,∠DAC = ∠EAB,AC = AB},
∴△DAC≌△EAB(SAS),
∴∠ADC = ∠AEB,CD = BE,故选项 A,D 不符合题意;
∵AC = AB,
∴∠ACB = ∠ABC.
∵∠CAB = ∠DAE = 36°,
∴∠ACB = ∠ABC = (180° - 36°)÷2 = 72°.
∵BE 平分∠ABC,
∴∠ABE = ∠CBE = 36°,
∴∠ACD = ∠ABE = 36°.
∵∠DCA = ∠CAB = 36°,
∴CD//AB,故选项 B 不符合题意;
根据已知条件无法证明 DE = GE. 故选项 C 符合题意. 故选 C.
知识拓展:本题主要考查了全等三角形的判定与性质、平行线的判定、角平分线的定义、三角形的内角和定理,证明△DAC≌△EAB 是解题的关键.
∵∠CAB = ∠DAE = 36°,
∴∠CAB - ∠CAE = ∠DAE - ∠CAE,即∠DAC = ∠EAB.
在△DAC 和△EAB 中,{AD = AE,∠DAC = ∠EAB,AC = AB},
∴△DAC≌△EAB(SAS),
∴∠ADC = ∠AEB,CD = BE,故选项 A,D 不符合题意;
∵AC = AB,
∴∠ACB = ∠ABC.
∵∠CAB = ∠DAE = 36°,
∴∠ACB = ∠ABC = (180° - 36°)÷2 = 72°.
∵BE 平分∠ABC,
∴∠ABE = ∠CBE = 36°,
∴∠ACD = ∠ABE = 36°.
∵∠DCA = ∠CAB = 36°,
∴CD//AB,故选项 B 不符合题意;
根据已知条件无法证明 DE = GE. 故选项 C 符合题意. 故选 C.
知识拓展:本题主要考查了全等三角形的判定与性质、平行线的判定、角平分线的定义、三角形的内角和定理,证明△DAC≌△EAB 是解题的关键.
9. 已知命题:“如果两个三角形全等,那么这两个三角形的面积相等.”写出它的逆命题:
如果两个三角形的面积相等,那么这两个三角形全等
,该逆命题是假
(填“真”或“假”)命题.答案:如果两个三角形的面积相等,那么这两个三角形全等 假
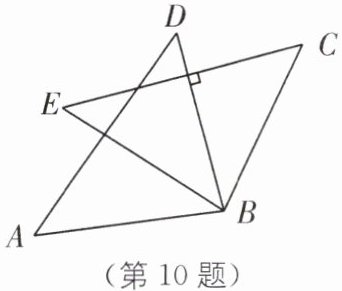
10.(2025·扬州邗江区期中)如图,△ADB≌△ECB,若$∠CBD= 40^\circ,$BD⊥EC,则∠D 的度数为______.

50°
答案:50° [解析]
∵∠CBD = 40°,BD⊥EC,
∴∠C = 90° - ∠CBD = 90° - 40° = 50°.
∵△ADB≌△ECB,
∴∠D = ∠C = 50°.
∵∠CBD = 40°,BD⊥EC,
∴∠C = 90° - ∠CBD = 90° - 40° = 50°.
∵△ADB≌△ECB,
∴∠D = ∠C = 50°.