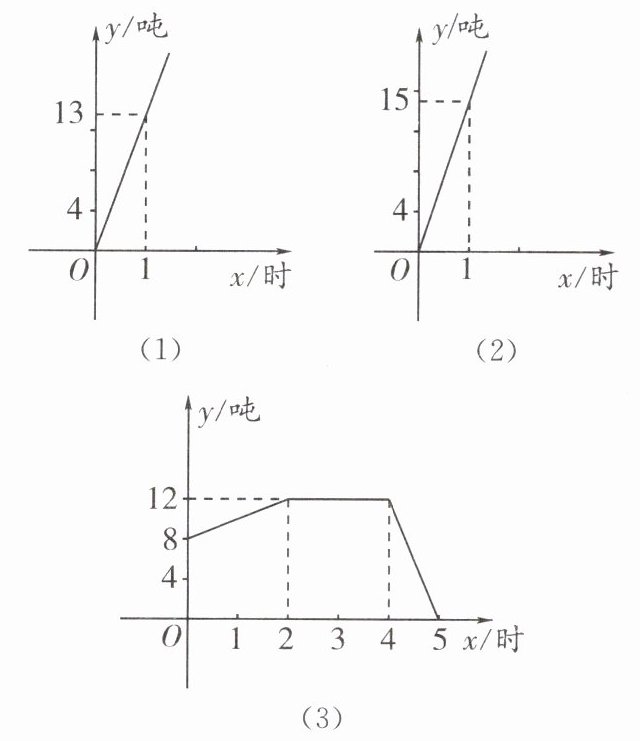
【例】(第二十届省初中数学竞赛)某仓储系统有20条输入传送带、20条输出传送带.某日,控制室的电脑显示,每条输入传送带每小时进库的货物流量如图(1),每条输出传送带每小时出库的货物流量如图(2),而该日仓库中原有货物8吨,在0时至5时,仓库中货物存量变化情况如图(3),则在0时至2时有多少条输入传送带和输出传送带在工作？在4时至5时有多少条输入传送带和输出传送带在工作？
解析：由图(1)可知,每条输入传送带每小时进库的货物流量为13吨；由图(2)可知,每条输出传送带每小时出库的货物流量为15吨.根据图(3)中货物存量变化列出方程求解即可.
答案：设0时至2时有a条输入传送带和b条输出传送带同时工作,则2(13a - 15b)= 4,即13a - 15b= 2.∵a,b为正整数,∴求出此方程的正整数解为a= 14,b= 12.再设4时至5时有m条输入传送带和n条输出传送带同时工作,则13m= 15n - 12,即15n - 13m= 12.∵m,n为正整数,∴求出此方程的正整数解为m= 6,n= 6.故0时至2时有14条输入传送带,12条输出传送带在工作；4时至5时有6条输入传送带,6条输出传送带在工作.
解析：由图(1)可知,每条输入传送带每小时进库的货物流量为13吨；由图(2)可知,每条输出传送带每小时出库的货物流量为15吨.根据图(3)中货物存量变化列出方程求解即可.答案：设0时至2时有a条输入传送带和b条输出传送带同时工作,则2(13a - 15b)= 4,即13a - 15b= 2.∵a,b为正整数,∴求出此方程的正整数解为a= 14,b= 12.再设4时至5时有m条输入传送带和n条输出传送带同时工作,则13m= 15n - 12,即15n - 13m= 12.∵m,n为正整数,∴求出此方程的正整数解为m= 6,n= 6.故0时至2时有14条输入传送带,12条输出传送带在工作；4时至5时有6条输入传送带,6条输出传送带在工作.
答案：【解析】：
本题可根据每条输入传送带和输出传送带每小时的货物流量，结合不同时间段内仓库货物存量的变化情况列出方程，再根据$a$、$b$、$m$、$n$为正整数来求解方程。
由图$(1)$可知，当$x = 1$时，$y = 13$，这表明每条输入传送带每小时进库的货物流量为$13$吨；由图$(2)$可知，当$x = 1$时，$y = 15$，即每条输出传送带每小时出库的货物流量为$15$吨。
在$0$时至$2$时，设$a$条输入传送带和$b$条输出传送带同时工作，$2$小时内输入的货物总量为$13a×2$吨，输出的货物总量为$15b×2$吨，而该时段内货物存量增加了$12 - 8 = 4$吨，原有货物$8$吨，所以可列方程$2(13a - 15b)= 4$，化简得到$13a - 15b = 2$。
因为$a$、$b$为正整数，通过试值法可求出此方程的正整数解为$a = 14$，$b = 12$。
在$4$时至$5$时，设$m$条输入传送带和$n$条输出传送带同时工作，$1$小时内输入的货物总量为$13m$吨，输出的货物总量为$15n$吨，该时段内货物存量减少了$12 - 0 = 12$吨，所以可列方程$13m = 15n - 12$，移项得到$15n - 13m = 12$。
由于$m$、$n$为正整数，同样通过试值法可求出此方程的正整数解为$m = 6$，$n = 6$。
【答案】：
解：由图$(1)$可知每条输入传送带每小时进库的货物流量为$13$吨；由图$(2)$可知每条输出传送带每小时出库的货物流量为$15$吨。
设$0$时至$2$时有$a$条输入传送带和$b$条输出传送带同时工作，则$2(13a - 15b)= 12 - 8$，即$13a - 15b = 2$。
因为$a$、$b$为正整数，所以此方程的正整数解为$a = 14$，$b = 12$。
再设$4$时至$5$时有$m$条输入传送带和$n$条输出传送带同时工作，则$13m = 15n - 12$，即$15n - 13m = 12$。
因为$m$、$n$为正整数，所以此方程的正整数解为$m = 6$，$n = 6$。
故$0$时至$2$时有$14$条输入传送带，$12$条输出传送带在工作；$4$时至$5$时有$6$条输入传送带，$6$条输出传送带在工作。
本题可根据每条输入传送带和输出传送带每小时的货物流量，结合不同时间段内仓库货物存量的变化情况列出方程，再根据$a$、$b$、$m$、$n$为正整数来求解方程。
由图$(1)$可知，当$x = 1$时，$y = 13$，这表明每条输入传送带每小时进库的货物流量为$13$吨；由图$(2)$可知，当$x = 1$时，$y = 15$，即每条输出传送带每小时出库的货物流量为$15$吨。
在$0$时至$2$时，设$a$条输入传送带和$b$条输出传送带同时工作，$2$小时内输入的货物总量为$13a×2$吨，输出的货物总量为$15b×2$吨，而该时段内货物存量增加了$12 - 8 = 4$吨，原有货物$8$吨，所以可列方程$2(13a - 15b)= 4$，化简得到$13a - 15b = 2$。
因为$a$、$b$为正整数，通过试值法可求出此方程的正整数解为$a = 14$，$b = 12$。
在$4$时至$5$时，设$m$条输入传送带和$n$条输出传送带同时工作，$1$小时内输入的货物总量为$13m$吨，输出的货物总量为$15n$吨，该时段内货物存量减少了$12 - 0 = 12$吨，所以可列方程$13m = 15n - 12$，移项得到$15n - 13m = 12$。
由于$m$、$n$为正整数，同样通过试值法可求出此方程的正整数解为$m = 6$，$n = 6$。
【答案】：
解：由图$(1)$可知每条输入传送带每小时进库的货物流量为$13$吨；由图$(2)$可知每条输出传送带每小时出库的货物流量为$15$吨。
设$0$时至$2$时有$a$条输入传送带和$b$条输出传送带同时工作，则$2(13a - 15b)= 12 - 8$，即$13a - 15b = 2$。
因为$a$、$b$为正整数，所以此方程的正整数解为$a = 14$，$b = 12$。
再设$4$时至$5$时有$m$条输入传送带和$n$条输出传送带同时工作，则$13m = 15n - 12$，即$15n - 13m = 12$。
因为$m$、$n$为正整数，所以此方程的正整数解为$m = 6$，$n = 6$。
故$0$时至$2$时有$14$条输入传送带，$12$条输出传送带在工作；$4$时至$5$时有$6$条输入传送带，$6$条输出传送带在工作。
1.[全国初中数学竞赛(海南赛区)初赛]若bk＜0,则直线y= kx + b一定通过(
A.第一、二象限
B.第二、三象限
C.第三、四象限
D.第一、四象限
D
).A.第一、二象限
B.第二、三象限
C.第三、四象限
D.第一、四象限
答案：1.D [解析]
∵bk＜0,
∴b＞0,k＜0或b＜0,k＞0.①当b＞0,k＜0时,直线y=kx+b经过第一、二、四象限;②当b＜0,k＞0时,直线y=kx+b经过第一、三、四象限.综上所述,直线y=kx+b一定经过第一、四象限.故选D.
∵bk＜0,
∴b＞0,k＜0或b＜0,k＞0.①当b＞0,k＜0时,直线y=kx+b经过第一、二、四象限;②当b＜0,k＞0时,直线y=kx+b经过第一、三、四象限.综上所述,直线y=kx+b一定经过第一、四象限.故选D.
2.[全国初中数学竞赛(天津赛区)初赛]某个一次函数的图象与直线y= $\frac{1}{2}$x + 3平行,与x轴、y轴的交点分别为A,B,并且过点(-2,-4),则在线段AB上(包括点A,B),横、纵坐标都是整数的点有(
A.3个
B.4个
C.5个
D.6个
B
).A.3个
B.4个
C.5个
D.6个
答案：2.B [解析]根据题意,设一次函数的表达式为y=$\frac{1}{2}$x+b,由点(-2,-4)在该函数图象上,得-4=$\frac{1}{2}$×(-2)+b,解得b=-3,
∴y=$\frac{1}{2}$x-3.
∴点A(6,0),B(0,-3).由0≤x≤6,且x为整数,取x=0,2,4,6时,对应的y值是整数.因此,在线段AB上(包括点A,B),横、纵坐标都是整数的点有4个.故选B.
∴y=$\frac{1}{2}$x-3.
∴点A(6,0),B(0,-3).由0≤x≤6,且x为整数,取x=0,2,4,6时,对应的y值是整数.因此,在线段AB上(包括点A,B),横、纵坐标都是整数的点有4个.故选B.
3.(四川省初中数学联赛初赛)某服装车间接到一批支援灾区的紧急生产任务,要求在一个月时间内生产尽可能多的套装(1件衣和1条裤为1套).已知第一小组甲、乙、丙、丁四个工人生产衣和裤的能力如下：一天时间甲可做衣4件或裤4条,乙可做衣9件或裤7条,丙可做衣6件或裤8条,丁可做衣11件或裤8条.问：怎样安排生产可使一周(7天)内生产的服装套数最多(因原料和设备安排,每位工人必须全天做衣或全天做裤)？最多是多少套？
答案：3.由题意可知,要尽可能多生产,应安排丁全部做衣,丙全部做裤.设一周内甲做衣x天,则做裤(7-x)天,乙做裤y天,则做衣(7-y)天,由题意,得4x+9(7-y)+11×7=4(7-x)+7y+8×7,整理,得x=2y-7.设一周生产的服装套数为W,则W=4x+9(7-y)+11×7=112-y,
∴W随着y的增大而减小.
∵x,y都是正整数,由x=2y-7,得y≥4,
∴当y=4时,W最大,此时W=108,x=1.
∴应当安排甲做1天衣,6天裤;乙做3天衣,4天裤;丙做7天裤;丁做7天衣,这时一周生产的服装套数最多,为108套.
∴W随着y的增大而减小.
∵x,y都是正整数,由x=2y-7,得y≥4,
∴当y=4时,W最大,此时W=108,x=1.
∴应当安排甲做1天衣,6天裤;乙做3天衣,4天裤;丙做7天裤;丁做7天衣,这时一周生产的服装套数最多,为108套.