6.(2024·北京通州区一模)在平面直角坐标系xOy中,函数$y = kx + b(k \neq 0)$的图象经过点A(0,-1)和B(4,3),与过点(0,-3)且平行于x轴的直线交于点C,当$x>-2$时,对于x的每一个值,函数$y = mx(m \neq 0)的值大于函数y = kx + b(k \neq 0)$的值,写出m的取值范围为______
1≤m≤3/2
.答案:1≤m≤3/2 [解析]将点A(0,-1)和B(4,3)代入y=kx+b(k≠0),得{b=-1,4k+b=3,解得{k=1,b=-1.则函数的表达式为y=x-1.过点(0,-3)且平行于x轴的直线为y=-3.
∵函数y=kx+b(k≠0)的图象经过点A(0,-1)和B(4,3),与过点(0,-3)且平行于x轴的直线交于点C,
∴x-1=-3,解得x=-2,即C(-2,-3).当直线y=mx(m≠0)过点C时,即把C(-2,-3)代入y=mx(m≠0),得-2m=-3,解得m=3/2.
∵当x>-2时,对于x的每一个值,y=mx(m≠0)的值大于y=x-1的值,
∴-2m≥-2-1,解得m≤3/2;当y=mx(m≠0)与直线y=x-1平行时,m=1,此时,满足条件,且当m<1时,不满足条件,
∴1≤m≤3/2. 思路引导 本题考查了待定系数法求一次函数表达式、一次函数的图象与性质,先求出y=kx+b(k≠0)的表达式,分情况讨论:当直线y=mx(m≠0)过点C时和当直线y=mx(m≠0)与直线y=kx+b(k≠0)平行时,即可得到符合条件的m的取值范围.
∵函数y=kx+b(k≠0)的图象经过点A(0,-1)和B(4,3),与过点(0,-3)且平行于x轴的直线交于点C,
∴x-1=-3,解得x=-2,即C(-2,-3).当直线y=mx(m≠0)过点C时,即把C(-2,-3)代入y=mx(m≠0),得-2m=-3,解得m=3/2.
∵当x>-2时,对于x的每一个值,y=mx(m≠0)的值大于y=x-1的值,
∴-2m≥-2-1,解得m≤3/2;当y=mx(m≠0)与直线y=x-1平行时,m=1,此时,满足条件,且当m<1时,不满足条件,
∴1≤m≤3/2. 思路引导 本题考查了待定系数法求一次函数表达式、一次函数的图象与性质,先求出y=kx+b(k≠0)的表达式,分情况讨论:当直线y=mx(m≠0)过点C时和当直线y=mx(m≠0)与直线y=kx+b(k≠0)平行时,即可得到符合条件的m的取值范围.
7. 已知一次函数$y = kx + b的图象平行于y = -2x + 1$,且过点(2,-1).
(1)求这个一次函数的表达式.
(2)当$x = 1$时,求y的值;当$y = 2$时,求x的值.
(3)画出该一次函数的图象.
(4)根据图象回答:当x取何值时,$y>0$;$y = 0$;$y<0$?
(1)求这个一次函数的表达式.
(2)当$x = 1$时,求y的值;当$y = 2$时,求x的值.
(3)画出该一次函数的图象.
(4)根据图象回答:当x取何值时,$y>0$;$y = 0$;$y<0$?
答案:
(1)根据题意,设这个一次函数的表达式为y=-2x+b,将点(2,-1)代入y=-2x+b,得b=3,则一次函数的表达式为y=-2x+3.
(2)由
(1),得一次函数的表达式为y=-2x+3,当x=1时,y=-2×1+3=1;当y=2时,则-2x+3=2,解得x=1/2.
(3)当x=0时,y=3,当y=0时,x=3/2,函数图象如图所示: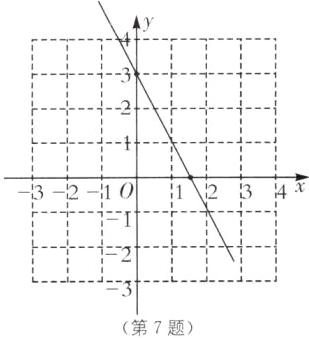
(4)根据图象,得当x<3/2时,y>0;当x=3/2时,y=0;当x>3/2时,y<0. 归纳总结 本题考查一次函数图象的运用及函数表达式的求法,解题时注意数形结合思想的运用.
(1)根据题意,设这个一次函数的表达式为y=-2x+b,将点(2,-1)代入y=-2x+b,得b=3,则一次函数的表达式为y=-2x+3.
(2)由
(1),得一次函数的表达式为y=-2x+3,当x=1时,y=-2×1+3=1;当y=2时,则-2x+3=2,解得x=1/2.
(3)当x=0时,y=3,当y=0时,x=3/2,函数图象如图所示:

(4)根据图象,得当x<3/2时,y>0;当x=3/2时,y=0;当x>3/2时,y<0. 归纳总结 本题考查一次函数图象的运用及函数表达式的求法,解题时注意数形结合思想的运用.
8. 如图,直线$l_1:y = \dfrac{5}{3}x + \dfrac{1}{3}与直线l_2:mx + ny = 5$交于点A(1,2),则方程组$\begin{cases}5x - 3y = -1 \\ mx + ny = 5\end{cases} $的解是(
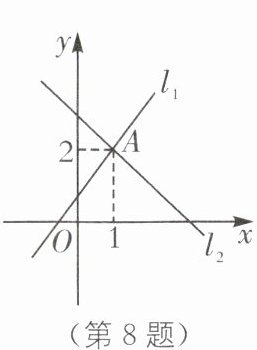
A.$\begin{cases}x = 1 \\ y = 2\end{cases} $
B.$\begin{cases}x = 2 \\ y = 1\end{cases} $
C.$\begin{cases}x = -1 \\ y = -2\end{cases} $
D.$\begin{cases}x = -2 \\ y = -1\end{cases} $
]
A
).
A.$\begin{cases}x = 1 \\ y = 2\end{cases} $
B.$\begin{cases}x = 2 \\ y = 1\end{cases} $
C.$\begin{cases}x = -1 \\ y = -2\end{cases} $
D.$\begin{cases}x = -2 \\ y = -1\end{cases} $
]
答案:A [解析]
∵直线l₁:y=5/3x+1/3与直线l₂:mx+ny=5交于点A(1,2),
∴方程组{y=5/3x+1/3,mx+ny=5的解为{x=1,y=2.即方程组{5x-3y=-1,mx+ny=5的解为{x=1,y=2.故选A.
∵直线l₁:y=5/3x+1/3与直线l₂:mx+ny=5交于点A(1,2),
∴方程组{y=5/3x+1/3,mx+ny=5的解为{x=1,y=2.即方程组{5x-3y=-1,mx+ny=5的解为{x=1,y=2.故选A.
9. 如图,直线$y_1 = x + 3$分别与x轴,y轴交于点A和点C,直线$y_2 = -x + 3$分别与x轴,y轴交于点B和点C,点P(m,1)是△ABC内部(包括边上)的一点,则m的最大值与最小值之差为
4
.答案:4 [解析]当y₁=1时,x+3=1,解得x=-2;当y₂=1时,-x+3=1,解得x=2.
∴-2≤m≤2,即m的最大值与最小值之差为2-(-2)=4.
∴-2≤m≤2,即m的最大值与最小值之差为2-(-2)=4.
10. 如图,直线$l_1:y = x + 1与直线l_2:y = -2x + n$相交于点P(1,b).
(1)求点P的坐标;
(2)点D(m,0)为x轴上的一个动点,过点D作x轴的垂线分别交$l_1和l_2$于点E,F,当$EF = 3$时,求m的值.
]

(1)求点P的坐标;
(2)点D(m,0)为x轴上的一个动点,过点D作x轴的垂线分别交$l_1和l_2$于点E,F,当$EF = 3$时,求m的值.
]

答案:
(1)
∵直线l₁:y=x+1过点P(1,b),
∴b=1+1=2,
∴P(1,2).
(2)将P(1,2)代入y=-2x+n,得-2+n=2,
∴n=4.把x=m分别代入直线l₁:y=x+1与直线l₂:y=-2x+4,得E(m,m+1),F(m,-2m+4).
∵EF=3,
∴当m>1时,EF=m+1-(-2m+4)=3,
∴m=2;当m<1时,-2m+4-m-1=3,
∴m=0.综上,m的值为2或0. 思路引导 本题考查两条直线相交的问题,一次函数与一元一次方程,关键是掌握待定系数法求一次函数表达式,掌握凡是函数图象经过的点必能满足表达式即可.
(1)把P点坐标代入y=x+1可得b的值;
(2)分两种情况:当m>1时,当m<1时,根据题意列出关于m的方程,解方程即可求得m的值.
(1)
∵直线l₁:y=x+1过点P(1,b),
∴b=1+1=2,
∴P(1,2).
(2)将P(1,2)代入y=-2x+n,得-2+n=2,
∴n=4.把x=m分别代入直线l₁:y=x+1与直线l₂:y=-2x+4,得E(m,m+1),F(m,-2m+4).
∵EF=3,
∴当m>1时,EF=m+1-(-2m+4)=3,
∴m=2;当m<1时,-2m+4-m-1=3,
∴m=0.综上,m的值为2或0. 思路引导 本题考查两条直线相交的问题,一次函数与一元一次方程,关键是掌握待定系数法求一次函数表达式,掌握凡是函数图象经过的点必能满足表达式即可.
(1)把P点坐标代入y=x+1可得b的值;
(2)分两种情况:当m>1时,当m<1时,根据题意列出关于m的方程,解方程即可求得m的值.