1. 如图为函数$y = kx + b(k,b$为常数,$k \neq 0)$的图象,则关于x的方程$kx + b = 3$的解为(
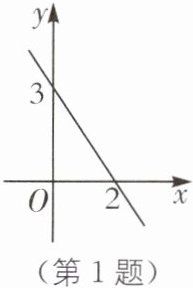
A.$x = 0$
B.$x = 2$
C.$x = 3$
D.无法确定
]
A
).A.$x = 0$
B.$x = 2$
C.$x = 3$
D.无法确定
]
答案：A [解析]观察函数的图象,得y=kx+b的图象经过点(0,3),即当x=0时y=kx+b=3,所以关于x的方程kx+b=3的解为x=0.故选A.
2. 已知一次函数$y = kx + b$的图象如图所示,则下列判断中正确的是(
A.$k＞0,b＜0$
B.y随x的增大而减小
C.当$x＞-3$时,$y＜0$
D.方程$kx + b = 0的解是x = -3$
]
D
).A.$k＞0,b＜0$
B.y随x的增大而减小
C.当$x＞-3$时,$y＜0$
D.方程$kx + b = 0的解是x = -3$
]
答案：D [解析]由图象可得A. k＞0,b＞0,故A选项错误,不符合题意;B. y随x的增大而增大,故B选项错误,不符合题意;C. 当x＞-3时,y＞0,故C选项错误,不符合题意;D. 一次函数y=kx+b与x轴的交点为(-3,0),即方程kx+b=0的解是x=-3,故D选项正确,符合题意.故选D.
3. 如图,已知一次函数$y = kx + b$的图象与x轴、y轴分别交于点(2,0),点(0,3),有下列结论：①图象经过点(1,-3)；②关于x的方程$kx + b = 0的解为x = 2$；③关于x的方程$kx + b = 3的解为x = 0$；④当$x＞2$时,$y＜0$. 其中正确的是______
]
②③④
.]
答案：②③④ [解析]把点(2,0),(0,3)代入y=kx+b,得{2k+b=0,b=3,解得{k=-3/2,b=3.
∴一次函数的表达式为y=-3/2x+3.当x=1时,y=3/2.
∴图象不经过点(1,-3),故①不符合题意;由图象得关于x的方程kx+b=0的解为x=2,故②符合题意;关于x的方程kx+b=3的解为x=0,故③符合题意;当x＞2时,y＜0,故④符合题意.故正确的有②③④.
∴一次函数的表达式为y=-3/2x+3.当x=1时,y=3/2.
∴图象不经过点(1,-3),故①不符合题意;由图象得关于x的方程kx+b=0的解为x=2,故②符合题意;关于x的方程kx+b=3的解为x=0,故③符合题意;当x＞2时,y＜0,故④符合题意.故正确的有②③④.
4. 分类讨论思想 如图,在平面直角坐标系中,一次函数$y = 2x - 2$的图象与x轴、y轴分别交于点A,B,一次函数$y = kx + b(k \neq 0)$的图象与x轴、y轴分别交于点C,D,且这两个函数图象交于点P,$OC = OD = 4OA$,连接OP,BC.
(1)直接写出C,D两点的坐标：C(______,______),D(______,______);
(2)求四边形OBCP的面积；
(3)若直线AB上存在一点Q,使得$S_{\triangle PQC}= S_{四边形OBCP}$,求点Q的坐标.
]
(1)直接写出C,D两点的坐标：C(______,______),D(______,______);
(2)求四边形OBCP的面积；
(3)若直线AB上存在一点Q,使得$S_{\triangle PQC}= S_{四边形OBCP}$,求点Q的坐标.
]
答案：
(1)4 0 0 4 [解析]将y=0代入一次函数y=2x-2中,得2x-2=0,解得x=1,
∴A(1,0).
∴OA=1.
∴OC=OD=4OA=4.
∴C(4,0),D(0,4).
(2)
∵一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于点C,D,
∴由
(1)可得{4k+b=0,b=4,解得{k=-1,b=4.
∴直线CD的表达式为y=-x+4.在一次函数y=2x-2中,令x=0,则y=-2.
∴点B的坐标为(0,-2).联立{y=2x-2,y=-x+4,解得{x=2,y=2.
∴点P的坐标为(2,2).
∴S四边形OBCP=1/2OC·|yP|+1/2OC·OB=1/2×4×2+1/2×4×2=8.
(3)
∵点Q在直线AB上,
∴设点Q为(a,2a-2).分为以下两种情况讨论:当点Q在点P的下方时,如图中Q₁所示.由
(1),
(2)可得,AC=3,点P的坐标为(2,2),
∴S△PQ₁C=1/2AC·|yP|+1/2AC·|yQ₁|=1/2×3×2+1/2×3×|2a-2|=3+3/2×|2a-2|.
∵S△PQ₁C=S四边形OBCP,
∴3+3/2×|2a-2|=8.
∴3/2(2-2a)=5,解得a=-2/3.
∴2a-2=2×(-2/3)-2=-10/3.
∴点Q₁的坐标为(-2/3,-10/3);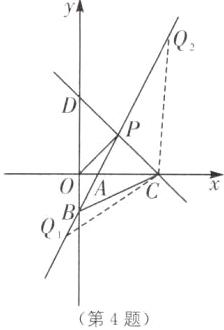
当点Q在点P的上方时,如图中Q₂所示.S△PQ₂C=1/2AC·|yQ₂|-1/2AC·|yP|=1/2×3×|2a-2|-1/2×3×2=3/2×|2a-2|-3.
∴3/2×|2a-2|-3=8.
∴3/2(2a-2)=11.解得a=14/3.
∴2a-2=2×14/3-2=22/3.
∴点Q₂的坐标为(14/3,22/3).综上所述,点Q的坐标为(-2/3,-10/3)或(14/3,22/3). 归纳总结 本题考查一次函数的图象及性质,熟练掌握一次函数的图象及性质、三角形的面积是解题的关键.
(1)4 0 0 4 [解析]将y=0代入一次函数y=2x-2中,得2x-2=0,解得x=1,
∴A(1,0).
∴OA=1.
∴OC=OD=4OA=4.
∴C(4,0),D(0,4).
(2)
∵一次函数y=kx+b(k≠0)的图象与x轴、y轴分别交于点C,D,
∴由
(1)可得{4k+b=0,b=4,解得{k=-1,b=4.
∴直线CD的表达式为y=-x+4.在一次函数y=2x-2中,令x=0,则y=-2.
∴点B的坐标为(0,-2).联立{y=2x-2,y=-x+4,解得{x=2,y=2.
∴点P的坐标为(2,2).
∴S四边形OBCP=1/2OC·|yP|+1/2OC·OB=1/2×4×2+1/2×4×2=8.
(3)
∵点Q在直线AB上,
∴设点Q为(a,2a-2).分为以下两种情况讨论:当点Q在点P的下方时,如图中Q₁所示.由
(1),
(2)可得,AC=3,点P的坐标为(2,2),
∴S△PQ₁C=1/2AC·|yP|+1/2AC·|yQ₁|=1/2×3×2+1/2×3×|2a-2|=3+3/2×|2a-2|.
∵S△PQ₁C=S四边形OBCP,
∴3+3/2×|2a-2|=8.
∴3/2(2-2a)=5,解得a=-2/3.
∴2a-2=2×(-2/3)-2=-10/3.
∴点Q₁的坐标为(-2/3,-10/3);
当点Q在点P的上方时,如图中Q₂所示.S△PQ₂C=1/2AC·|yQ₂|-1/2AC·|yP|=1/2×3×|2a-2|-1/2×3×2=3/2×|2a-2|-3.∴3/2×|2a-2|-3=8.
∴3/2(2a-2)=11.解得a=14/3.
∴2a-2=2×14/3-2=22/3.
∴点Q₂的坐标为(14/3,22/3).综上所述,点Q的坐标为(-2/3,-10/3)或(14/3,22/3). 归纳总结 本题考查一次函数的图象及性质,熟练掌握一次函数的图象及性质、三角形的面积是解题的关键.
5. 已知一次函数$y = mx + n(m＜0)$的图象经过点P(-2,3),则关于x的不等式$mx + n＞3$的解集为( ).
A.$x＞-3$
B.$x＜-3$
C.$x＞-2$
D.$x＜-2$
A.$x＞-3$
B.$x＜-3$
C.$x＞-2$
D.$x＜-2$
答案：
D [解析]
∵一次函数y=mx+n(m＜0)的图象经过点P(-2,3),
∴可画出y=mx+n(m＜0)的大致图象如图:
由图可知,当x＜-2时,mx+n＞3,
∴关于x的不等式mx+n＞3的解集为x＜-2.故选D.
D [解析]
∵一次函数y=mx+n(m＜0)的图象经过点P(-2,3),
∴可画出y=mx+n(m＜0)的大致图象如图:
由图可知,当x＜-2时,mx+n＞3,∴关于x的不等式mx+n＞3的解集为x＜-2.故选D.