7. 若直线$y= kx+3与直线y= 2x+b关于x$轴对称,则$k$,$b$的值分别为(
A.$k= -2$,$b= 3$
B.$k= 2$,$b= -3$
C.$k= -2$,$b= -3$
D.$k= 2$,$b= 3$
C
).A.$k= -2$,$b= 3$
B.$k= 2$,$b= -3$
C.$k= -2$,$b= -3$
D.$k= 2$,$b= 3$
答案:C
解析:
解:在直线$y = kx + 3$上取两点,当$x = 0$时,$y = 3$,得点$(0, 3)$;当$y = 0$时,$kx + 3 = 0$,解得$x=-\dfrac{3}{k}$,得点$\left(-\dfrac{3}{k}, 0\right)$。
因为两直线关于$x$轴对称,所以这两点关于$x$轴的对称点$(0, -3)$、$\left(-\dfrac{3}{k}, 0\right)$在直线$y = 2x + b$上。
将$(0, -3)$代入$y = 2x + b$,得$-3 = 2×0 + b$,解得$b=-3$。
将$\left(-\dfrac{3}{k}, 0\right)$代入$y = 2x - 3$,得$0 = 2×\left(-\dfrac{3}{k}\right)- 3$,即$-\dfrac{6}{k}- 3=0$,解得$k=-2$。
结论:$k = -2$,$b=-3$,选C。
因为两直线关于$x$轴对称,所以这两点关于$x$轴的对称点$(0, -3)$、$\left(-\dfrac{3}{k}, 0\right)$在直线$y = 2x + b$上。
将$(0, -3)$代入$y = 2x + b$,得$-3 = 2×0 + b$,解得$b=-3$。
将$\left(-\dfrac{3}{k}, 0\right)$代入$y = 2x - 3$,得$0 = 2×\left(-\dfrac{3}{k}\right)- 3$,即$-\dfrac{6}{k}- 3=0$,解得$k=-2$。
结论:$k = -2$,$b=-3$,选C。
8. 已知一次函数的图象$l经过点A(0,-2)$,且与正比例函数$y= \frac{1}{3}x的图象交于点(3,a)$.
(1)求一次函数表达式;
(2)若将直线$l$进行平移,使平移后的直线与坐标轴围成的三角形面积为15,求平移后的直线表达式.
(1)求一次函数表达式;
(2)若将直线$l$进行平移,使平移后的直线与坐标轴围成的三角形面积为15,求平移后的直线表达式.
答案:
(1)把(3,a)代入$y=\frac{1}{3}x,$解得a=1,
∴交点坐标为(3,1),设直线l的表达式为y=kx+b,把A(0,-2)和(3,1)代入得$\begin{cases}b=-2, \\3k+b=1,\end{cases}$解得$\begin{cases}k=1, \\b=-2,\end{cases}$
∴一次函数的表达式为y=x-2.
(2)设平移后的直线表达式为y=x+a,则其与x轴交点坐标为(-a,0),与y轴交点坐标为(0,a),
∴平移后的直线与坐标轴围成的三角形面积为$\frac{1}{2}a^{2}=15,$解得$a=±\sqrt{30},$
∴平移后的直线表达式为$y=x+\sqrt{30}$或$y=x-\sqrt{30}.$
(1)把(3,a)代入$y=\frac{1}{3}x,$解得a=1,
∴交点坐标为(3,1),设直线l的表达式为y=kx+b,把A(0,-2)和(3,1)代入得$\begin{cases}b=-2, \\3k+b=1,\end{cases}$解得$\begin{cases}k=1, \\b=-2,\end{cases}$
∴一次函数的表达式为y=x-2.
(2)设平移后的直线表达式为y=x+a,则其与x轴交点坐标为(-a,0),与y轴交点坐标为(0,a),
∴平移后的直线与坐标轴围成的三角形面积为$\frac{1}{2}a^{2}=15,$解得$a=±\sqrt{30},$
∴平移后的直线表达式为$y=x+\sqrt{30}$或$y=x-\sqrt{30}.$
9. (2025·福建宁德期中)福鼎市贯岭镇是黄栀子之乡,今年黄栀子价格大涨,农民收益颇丰,某天一农户采收$A$级、$B$级黄栀子共200千克,$A$级黄栀子售价每千克8元,$B$级黄栀子售价每千克6元.
(1)求该农户全部售出这些黄栀子的收入$y$(元)与采收的$A级黄栀子数量x$(千克)之间的函数表达式;
(2)若当天全部售出这些黄栀子的总收入为1440元,求售出的$A$级黄栀子的数量.
(1)求该农户全部售出这些黄栀子的收入$y$(元)与采收的$A级黄栀子数量x$(千克)之间的函数表达式;
(2)若当天全部售出这些黄栀子的总收入为1440元,求售出的$A$级黄栀子的数量.
答案:
(1)依题意,得y=8x+6(200-x),即y=2x+1200.
(2)当y=1440时,可得2x+1200=1440,解得x=120.故收入1440元时,售出A级黄栀子120千克.
(1)依题意,得y=8x+6(200-x),即y=2x+1200.
(2)当y=1440时,可得2x+1200=1440,解得x=120.故收入1440元时,售出A级黄栀子120千克.
10. (2025·广西期中)甲村和乙村共有22000吨小麦需要分别运往$A$,$B$两地,其运费单价如下表:
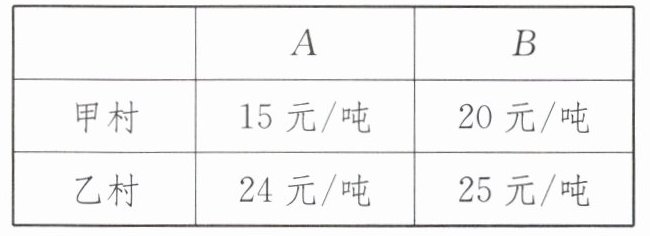
若将甲村的小麦全部运往$B$地,乙村的小麦全部运往$A$地,则所需运费相同.
(1)求甲、乙两村各需要运输多少吨小麦?
(2)若甲、乙两村需要给$A$地运输小麦共9000吨,且甲村最多只能给$A$地运输5000吨小麦,请问怎么调运可使运费最少?并求出最少运费.

若将甲村的小麦全部运往$B$地,乙村的小麦全部运往$A$地,则所需运费相同.
(1)求甲、乙两村各需要运输多少吨小麦?
(2)若甲、乙两村需要给$A$地运输小麦共9000吨,且甲村最多只能给$A$地运输5000吨小麦,请问怎么调运可使运费最少?并求出最少运费.
答案:
(1)设甲村需要运输x吨小麦,乙村需要运输y吨小麦,依题意,得$\begin{cases}x+y=22000, \\20x=24y,\end{cases}$解得$\begin{cases}x=12000, \\y=10000.\end{cases}$故甲村需要运输12000吨小麦,乙村需要运输10000吨小麦.
(2)设甲村给A地运输m吨小麦,总运费为w元,则甲村给B地运输(12000-m)吨小麦,乙村给A地运输(9000-m)吨小麦,乙村给B地运输10000-(9000-m)=(1000+m)吨小麦,依题意,得w=15m+20(12000-m)+24(9000-m)+25(1000+m),即w=-4m+481000.
∵-4<0,
∴w随m的增大而减小.又m≤5000,
∴当m=5000时,w取得最小值,最小值为-4×5000+481000=461000,此时12000-m=12000-5000=7000,9000-m=9000-5000=4000,1000+m=1000+5000=6000.故当甲村给A地运输5000吨小麦,给B地运输7000吨小麦,乙村给A地运输4000吨小麦,给B地运输6000吨小麦时,总运费最少,最少运费为461000元.
(1)设甲村需要运输x吨小麦,乙村需要运输y吨小麦,依题意,得$\begin{cases}x+y=22000, \\20x=24y,\end{cases}$解得$\begin{cases}x=12000, \\y=10000.\end{cases}$故甲村需要运输12000吨小麦,乙村需要运输10000吨小麦.
(2)设甲村给A地运输m吨小麦,总运费为w元,则甲村给B地运输(12000-m)吨小麦,乙村给A地运输(9000-m)吨小麦,乙村给B地运输10000-(9000-m)=(1000+m)吨小麦,依题意,得w=15m+20(12000-m)+24(9000-m)+25(1000+m),即w=-4m+481000.
∵-4<0,
∴w随m的增大而减小.又m≤5000,
∴当m=5000时,w取得最小值,最小值为-4×5000+481000=461000,此时12000-m=12000-5000=7000,9000-m=9000-5000=4000,1000+m=1000+5000=6000.故当甲村给A地运输5000吨小麦,给B地运输7000吨小麦,乙村给A地运输4000吨小麦,给B地运输6000吨小麦时,总运费最少,最少运费为461000元.