1. 若函数$y= (k+3)x^{|k+2|}-5是关于x$的一次函数,则$k$的值是(
A.$-1$
B.$-3$
C.$-1或-3$
D.无法确定
A
).A.$-1$
B.$-3$
C.$-1或-3$
D.无法确定
答案:A [解析]
∵函数y=(k+3)x^{|k+2|}-5是关于x的一次函数,
∴|k+2|=1且k+3≠0,解得k=-1.故选A.
∵函数y=(k+3)x^{|k+2|}-5是关于x的一次函数,
∴|k+2|=1且k+3≠0,解得k=-1.故选A.
2. 若函数$y= (m+3)x^{2m+1}+4x-5(x≠0)$是一次函数,求$m$的值.
答案:
∵y=(m+3)x^{2m+1}+4x-5(x≠0)是一次函数,
∴分情况求解如下:
①当m+3=0时,解得m=-3;
②当2m+1=0时,解得$m=-\frac{1}{2};③$当2m+1=1且m+3+4≠0时,解得m=0.
综上所述,m的值为-3或$-\frac{1}{2}$或0.
∵y=(m+3)x^{2m+1}+4x-5(x≠0)是一次函数,
∴分情况求解如下:
①当m+3=0时,解得m=-3;
②当2m+1=0时,解得$m=-\frac{1}{2};③$当2m+1=1且m+3+4≠0时,解得m=0.
综上所述,m的值为-3或$-\frac{1}{2}$或0.
3. (2025·安徽阜阳月考)一次函数$y= 2kx-3的图象经过点(2,-5)$,则$k=$(
A.$2$
B.$-2$
C.$-\frac{1}{2}$
D.$\frac{1}{2}$
C
).A.$2$
B.$-2$
C.$-\frac{1}{2}$
D.$\frac{1}{2}$
答案:C [解析]
∵一次函数y=2kx-3的图象经过点(2,-5),
∴2k×2-3=-5,解得$k=-\frac{1}{2}.$故选C.
∵一次函数y=2kx-3的图象经过点(2,-5),
∴2k×2-3=-5,解得$k=-\frac{1}{2}.$故选C.
4. 已知一次函数$y= kx+b的图象经过点(-2,10)$,$(3,0)和(1,m)$.
(1)求$m$的值;
(2)当$-4\leq y\leq8$时,求$x$的取值范围.
(1)求$m$的值;
(2)当$-4\leq y\leq8$时,求$x$的取值范围.
答案:
(1)
∵一次函数y=kx+b的图象经过点(-2,10),(3,0),
∴$\begin{cases}-2k+b=10, \\3k+b=0,\end{cases}$解得$\begin{cases}k=-2, \\b=6,\end{cases}$
∴一次函数的表达式为y=-2x+6,
∴m=-2×1+6=4.
(2)
∵-2<0,
∴y随x的增大而减小.当y=-4时,-4=-2x+6,解得x=5;当y=8时,8=-2x+6,解得x=-1.
∴当-4≤y≤8时,x的取值范围为-1≤x≤5.
(1)
∵一次函数y=kx+b的图象经过点(-2,10),(3,0),
∴$\begin{cases}-2k+b=10, \\3k+b=0,\end{cases}$解得$\begin{cases}k=-2, \\b=6,\end{cases}$
∴一次函数的表达式为y=-2x+6,
∴m=-2×1+6=4.
(2)
∵-2<0,
∴y随x的增大而减小.当y=-4时,-4=-2x+6,解得x=5;当y=8时,8=-2x+6,解得x=-1.
∴当-4≤y≤8时,x的取值范围为-1≤x≤5.
5. 如图,一个正比例函数与一个一次函数的图象交于点$A(4,3)$,一次函数的图象与$y轴交于点B$,且$OA= OB$.
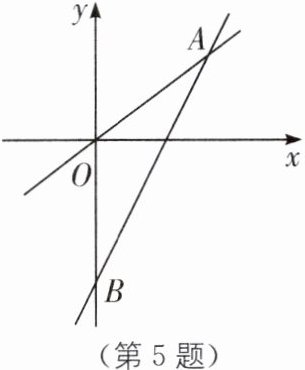
(1)求点$B$的坐标;
(2)求这两个函数的表达式.

(1)求点$B$的坐标;
(2)求这两个函数的表达式.
答案:
(1)
∵A(4,3),
∴$OA=\sqrt{3^{2}+4^{2}}=5.$
∵OA=OB,
∴OB=5,
∴点B的坐标为(0,-5).
(2)设正比例函数的表达式为y=mx,一次函数的表达式为y=kx+b.把A(4,3)代入y=mx,得4m=3,则$m=\frac{3}{4},$
∴正比例函数的表达式为$y=\frac{3}{4}x;$把A(4,3),B(0,-5)代入y=kx+b,得$\begin{cases}4k+b=3, \\b=-5,\end{cases}$解得$\begin{cases}k=2, \\b=-5,\end{cases}$
∴一次函数的表达式为y=2x-5.
(1)
∵A(4,3),
∴$OA=\sqrt{3^{2}+4^{2}}=5.$
∵OA=OB,
∴OB=5,
∴点B的坐标为(0,-5).
(2)设正比例函数的表达式为y=mx,一次函数的表达式为y=kx+b.把A(4,3)代入y=mx,得4m=3,则$m=\frac{3}{4},$
∴正比例函数的表达式为$y=\frac{3}{4}x;$把A(4,3),B(0,-5)代入y=kx+b,得$\begin{cases}4k+b=3, \\b=-5,\end{cases}$解得$\begin{cases}k=2, \\b=-5,\end{cases}$
∴一次函数的表达式为y=2x-5.
6. 甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,轿车比货车晚出发1.5小时,如图,线段$OA表示货车离甲地的距离y$(千米)与时间$x$(小时)之间的函数关系;折线$BCD表示轿车离甲地的距离y$(千米)与时间$x$(小时)之间的函数关系,请根据图象解答下列问题:

(1)轿车到达乙地时,求货车与甲地的距离.
(2)求线段$CD$对应的函数表达式.
(3)在轿车行进过程中,轿车行驶多少时间,两车相距30千米?

(1)轿车到达乙地时,求货车与甲地的距离.
(2)求线段$CD$对应的函数表达式.
(3)在轿车行进过程中,轿车行驶多少时间,两车相距30千米?
答案:
(1)由图象可得,货车的速度为300÷6=50(千米/时),则轿车到达乙地时,货车行驶了5小时,此时货车与甲地的距离是50×5=250(千米),故轿车到达乙地时,货车与甲地的距离是250千米.
(2)设线段CD对应的函数表达式是y=kx+b.
∵点C(3,90),点D(5,300),
∴$\begin{cases}3k+b=90, \\5k+b=300,\end{cases}$解得$\begin{cases}k=105, \\b=-225.\end{cases}$故线段CD对应的函数表达式是y=105x-225(3≤x≤5).
(3)当x=3时,两车之间的距离为50×3-90=60.
∵60>30,
∴在轿车行进过程中,两车相距30千米的时间在3~5之间,由图象,可得线段OA对应的函数表达式为y=50x,则|50x-(105x-225)|=30,解得$x_{1}=\frac{39}{11},x_{2}=\frac{51}{11}.$
∵轿车比货车晚出发1.5小时,
∴$\frac{39}{11}-1.5=\frac{45}{22}($小时$),\frac{51}{11}-1.5=\frac{69}{22}($小时),故在轿车行进过程中,轿车行驶$\frac{45}{22}$小时或$\frac{69}{22}$小时,两车相距30千米.
(1)由图象可得,货车的速度为300÷6=50(千米/时),则轿车到达乙地时,货车行驶了5小时,此时货车与甲地的距离是50×5=250(千米),故轿车到达乙地时,货车与甲地的距离是250千米.
(2)设线段CD对应的函数表达式是y=kx+b.
∵点C(3,90),点D(5,300),
∴$\begin{cases}3k+b=90, \\5k+b=300,\end{cases}$解得$\begin{cases}k=105, \\b=-225.\end{cases}$故线段CD对应的函数表达式是y=105x-225(3≤x≤5).
(3)当x=3时,两车之间的距离为50×3-90=60.
∵60>30,
∴在轿车行进过程中,两车相距30千米的时间在3~5之间,由图象,可得线段OA对应的函数表达式为y=50x,则|50x-(105x-225)|=30,解得$x_{1}=\frac{39}{11},x_{2}=\frac{51}{11}.$
∵轿车比货车晚出发1.5小时,
∴$\frac{39}{11}-1.5=\frac{45}{22}($小时$),\frac{51}{11}-1.5=\frac{69}{22}($小时),故在轿车行进过程中,轿车行驶$\frac{45}{22}$小时或$\frac{69}{22}$小时,两车相距30千米.