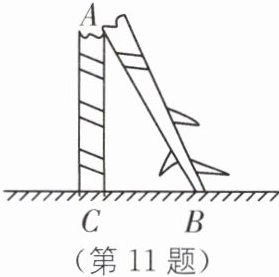
11.传统文化 折竹问题 (2024·淮安期末)折竹问题:今有竹高九尺,末折抵地,去根三尺,问折者高几何?意思是一根竹子原高9尺,中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?即:如图,$AB+AC= 9$尺,$BC= 3$尺,则AC的高为
4
尺.
答案:4 [解析]由题意知,AB + AC = 9尺,BC = 3尺.
在Rt△ABC中,由勾股定理,得$AB^2 = AC^2 + BC^2$,
即$(9 - AC)^2 = AC^2 + 9$,解得AC = 4.
在Rt△ABC中,由勾股定理,得$AB^2 = AC^2 + BC^2$,
即$(9 - AC)^2 = AC^2 + 9$,解得AC = 4.
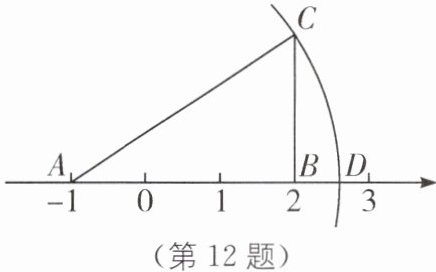
12.(2025·黑龙江大庆期末)如图,在数轴上,点A,B分别表示实数$-1$,2,过点B作$BC\perp AB$,且$BC= 2$,连接AC. 若以点A为圆心,AC长为半径画弧,交数轴正半轴于点D,则点D对应的实数是______
$\sqrt{13} - 1$
.
答案:$\sqrt{13} - 1$ [解析]
∵点A,B分别表示实数 - 1,2,
∴AB = |2 - (-1)| = |2 + 1| = 3.
∵BC⊥AB,
∴∠ABC = 90°,
∴$AC = \sqrt{AB^2 + BC^2} = \sqrt{3^2 + 2^2} = \sqrt{13}$,
由题意可知,AD = AC = $\sqrt{13}$
∵A点表示的数是 - 1,
设点D表示的数为x,
∴|x - (-1)| = $\sqrt{13}$
|x + 1| = $\sqrt{13}$,$x + 1 = ±\sqrt{13}$,
$x = \sqrt{13} - 1$或$-\sqrt{13} - 1$(不合题意,舍去),
∴点D表示的数为$\sqrt{13} - 1$.
归纳总结 本题主要考查了实数与数轴、勾股定理,解题关键是熟练掌握两点间的距离公式和勾股定理.
∵点A,B分别表示实数 - 1,2,
∴AB = |2 - (-1)| = |2 + 1| = 3.
∵BC⊥AB,
∴∠ABC = 90°,
∴$AC = \sqrt{AB^2 + BC^2} = \sqrt{3^2 + 2^2} = \sqrt{13}$,
由题意可知,AD = AC = $\sqrt{13}$
∵A点表示的数是 - 1,
设点D表示的数为x,
∴|x - (-1)| = $\sqrt{13}$
|x + 1| = $\sqrt{13}$,$x + 1 = ±\sqrt{13}$,
$x = \sqrt{13} - 1$或$-\sqrt{13} - 1$(不合题意,舍去),
∴点D表示的数为$\sqrt{13} - 1$.
归纳总结 本题主要考查了实数与数轴、勾股定理,解题关键是熟练掌握两点间的距离公式和勾股定理.
13.(2025·南京联合体期末)与$\sqrt{20}$最接近的整数是
4
.答案:4 [解析]
∵$\sqrt{16} < \sqrt{20} < \sqrt{20.25}$,
∴4 < $\sqrt{20} < 4.5$,
∴$\sqrt{20}$最接近的整数是4.
∵$\sqrt{16} < \sqrt{20} < \sqrt{20.25}$,
∴4 < $\sqrt{20} < 4.5$,
∴$\sqrt{20}$最接近的整数是4.
14.(2025·泰州姜堰区期末)若k,b都是实数,且$\sqrt{k-1}+\sqrt{1-k}+b= 3$,则$k+b= $
4
.答案:4 [解析]根据题意,得$\begin{cases}k - 1 \geq 0 \\ 1 - k \geq 0 \end{cases}$,
解得k = 1,
∴0 + 0 + b = 3,
∴b = 3,
∴k + b = 1 + 3 = 4.
解得k = 1,
∴0 + 0 + b = 3,
∴b = 3,
∴k + b = 1 + 3 = 4.
15.若$2a-1$和$5-a$是一个数m的平方根,则$a=$
-4
,$m=$81
.答案:- 4 81 [解析]由题意,得2a - 1 + 5 - a = 0,
解得a = - 4,则$m = (2a - 1)^2 = 81$.
解得a = - 4,则$m = (2a - 1)^2 = 81$.
16.(2024·陕西中考)如图,在$\triangle ABC$中,$AB= AC$,E是边AB上一点,连接CE,在BC的右侧作$BF// AC$,且$BF= AE$,连接CF. 若$AC= 13$,$BC= 10$,则四边形EBFC的面积为______

60
.
答案:60 [解析]
∵AB = AC,
∴∠ABC = ∠ACB.
∵BF//AC,
∴∠ACB = ∠CBF,
∴∠ABC = ∠CBF,
∴BC平分∠ABF.
如图,过点C作CM⊥AB于点M,CN⊥BF于点N,则CM = CN.
∵$S_{\triangle ACE} = \frac{1}{2}AE\cdot CM$,$S_{\triangle CBF} = \frac{1}{2}BF\cdot CN$,且BF = AE,
∴$S_{\triangle CBF} = S_{\triangle ACE}$,
∴四边形EBFC的面积 = $S_{\triangle CBF} + S_{\triangle CBE} = S_{\triangle ACE} + S_{\triangle CBE} = S_{\triangle CBA}$.
∵AC = 13,
∴AB = 13.
设AM = x,则BM = 13 - x,
由勾股定理,得$CM^2 = AC^2 - AM^2 = BC^2 - BM^2$,
∴$13^2 - x^2 = 10^2 - (13 - x)^2$,解得$x = \frac{119}{13}$,
∴$CM = \sqrt{13^2 - (\frac{119}{13})^2} = \frac{120}{13}$,
∴$S_{\triangle CBA} = \frac{1}{2}AB\cdot CM = 60$,
∴四边形EBFC的面积为60.
归纳总结 本题考查角平分线的性质、三角形的面积、勾股定理,关键是由三角形的面积得到$S_{\triangle CBF} = S_{\triangle ACE}$.
∵AB = AC,
∴∠ABC = ∠ACB.
∵BF//AC,
∴∠ACB = ∠CBF,
∴∠ABC = ∠CBF,
∴BC平分∠ABF.
如图,过点C作CM⊥AB于点M,CN⊥BF于点N,则CM = CN.
∵$S_{\triangle ACE} = \frac{1}{2}AE\cdot CM$,$S_{\triangle CBF} = \frac{1}{2}BF\cdot CN$,且BF = AE,
∴$S_{\triangle CBF} = S_{\triangle ACE}$,
∴四边形EBFC的面积 = $S_{\triangle CBF} + S_{\triangle CBE} = S_{\triangle ACE} + S_{\triangle CBE} = S_{\triangle CBA}$.
∵AC = 13,
∴AB = 13.
设AM = x,则BM = 13 - x,
由勾股定理,得$CM^2 = AC^2 - AM^2 = BC^2 - BM^2$,
∴$13^2 - x^2 = 10^2 - (13 - x)^2$,解得$x = \frac{119}{13}$,
∴$CM = \sqrt{13^2 - (\frac{119}{13})^2} = \frac{120}{13}$,
∴$S_{\triangle CBA} = \frac{1}{2}AB\cdot CM = 60$,
∴四边形EBFC的面积为60.
归纳总结 本题考查角平分线的性质、三角形的面积、勾股定理,关键是由三角形的面积得到$S_{\triangle CBF} = S_{\triangle ACE}$.
17.为了比较$\sqrt{5}+1与\sqrt{10}$的大小,可以构造如图所示的图形进行推算,其中$\angle C= 90^\circ$,$BC= 3$,点D在BC上且$BD= AC= 1$. 通过计算可得$\sqrt{5}+1$

>
$\sqrt{10}$.(填“>”“<”或“=”)
答案:> [解析]
∵∠C = 90°,BC = 3,BD = AC = 1,
∴CD = 2,
∴在Rt△ADC中,$AD = \sqrt{CD^2 + AC^2} = \sqrt{5}$,在Rt△ABC中,$AB = \sqrt{BC^2 + AC^2} = \sqrt{10}$
∴BD + AD = $\sqrt{5} + 1$.
在△ABD中,AD + BD>AB,
∴$\sqrt{5} + 1>\sqrt{10}$
归纳总结 本题主要考查了实数的大小比较、三角形三边关系以及勾股定理的运用,解题时注意:三角形任意两边之和大于第三边.
∵∠C = 90°,BC = 3,BD = AC = 1,
∴CD = 2,
∴在Rt△ADC中,$AD = \sqrt{CD^2 + AC^2} = \sqrt{5}$,在Rt△ABC中,$AB = \sqrt{BC^2 + AC^2} = \sqrt{10}$
∴BD + AD = $\sqrt{5} + 1$.
在△ABD中,AD + BD>AB,
∴$\sqrt{5} + 1>\sqrt{10}$
归纳总结 本题主要考查了实数的大小比较、三角形三边关系以及勾股定理的运用,解题时注意:三角形任意两边之和大于第三边.
18.如图,已知在$\triangle ABC$中,$AB= 6$,$AC= 8$,$BC= 10$,P为边BC上的一个动点,连接AP,$DE\perp AP$,分别交AB,AC于点D,E,垂足为M,点N为DE的中点,若四边形ADPE的面积为18,则AN的最大值为______

$\frac{15}{4}$
.
答案:$\frac{15}{4}$ [解析]
∵在△ABC中,AB = 6,AC = 8,BC = 10,
∴$AB^2 + AC^2 = BC^2$,
∴△ABC为直角三角形,且∠BAC = 90°.
∵N为DE的中点,
∴$AN = \frac{1}{2}DE$.
∵四边形ADPE的面积为18,DE⊥AP,
∴$\frac{1}{2}DE\cdot AP = 18$,即AN·AP = 18,
∴当AP取最小值时,AN有最大值,
故当AP⊥BC时,AP值最小,最小值为$\frac{6×8}{10} = \frac{24}{5}$,
此时$AN = 18÷\frac{24}{5} = \frac{15}{4}$.
∵在△ABC中,AB = 6,AC = 8,BC = 10,
∴$AB^2 + AC^2 = BC^2$,
∴△ABC为直角三角形,且∠BAC = 90°.
∵N为DE的中点,
∴$AN = \frac{1}{2}DE$.
∵四边形ADPE的面积为18,DE⊥AP,
∴$\frac{1}{2}DE\cdot AP = 18$,即AN·AP = 18,
∴当AP取最小值时,AN有最大值,
故当AP⊥BC时,AP值最小,最小值为$\frac{6×8}{10} = \frac{24}{5}$,
此时$AN = 18÷\frac{24}{5} = \frac{15}{4}$.
19.(2024·滨州中考)计算:$2^{-1}+(-2)×(-\frac{1}{2})-\sqrt{\frac{9}{4}}$.
答案:原式 = $\frac{1}{2} + 1 - \frac{3}{2} = 0$.
20.在如图所示的数轴上画出表示下列各数的点,并用“<”号将这些数按从小到大的顺序连接起来.
$-|-3.5|$,$1\frac{1}{2}$,0,$-(-2\frac{1}{2})$,$+(-1)$,$(-2)^2$.

$-|-3.5|$,$1\frac{1}{2}$,0,$-(-2\frac{1}{2})$,$+(-1)$,$(-2)^2$.

答案:- | - 3.5| = - 3.5,$-(-2\frac{1}{2}) = 2\frac{1}{2}$,$+( - 1) = - 1$,$(-2)^2 = 4$,在数轴上画出表示各数的点如图所示:
∴ - | - 3.5| < +( - 1) < 0 < $1\frac{1}{2}$ < $-(-2\frac{1}{2})$ < $(-2)^2$.
∴ - | - 3.5| < +( - 1) < 0 < $1\frac{1}{2}$ < $-(-2\frac{1}{2})$ < $(-2)^2$.
21.(2025·徐州期末)如图,在长方形ABCD中,$AB= 4$,$AD= 5$,E为BC上的点. 将$\triangle ABE$沿AE折叠,使点B落在长方形内的点F处. 连接DF,已知$DF= 3$.
(1)求证:$\triangle ADF$为直角三角形;
(2)求线段BE的长.

(1)求证:$\triangle ADF$为直角三角形;
(2)求线段BE的长.

答案:
(1)
∵将△ABE沿AE折叠,使点B落在长方形内的点F处,AB = 4,
∴AB = AF = 4,
在△ADF中,AD = 5,DF = 3,且$3^2 + 4^2 = 5^2$,
∴$FD^2 + AF^2 = AD^2$,
∴△ADF是直角三角形.
(2)由
(1)知,∠AFD = 90°.
设BE = x,则EF = x,
根据折叠可知,∠AFE = ∠B = 90°.
∵∠AFD = 90°,
∴∠DFE = 180°,
∴D,F,E三点在同一条直线上,
∴DE = 3 + x,
CE = 5 - x,DC = AB = 4,
在Rt△DCE中,根据勾股定理,得$DE^2 = DC^2 + EC^2$,
∴$(3 + x)^2 = 4^2 + (5 - x)^2$,解得x = 2.
故BE的长为2.
(1)
∵将△ABE沿AE折叠,使点B落在长方形内的点F处,AB = 4,
∴AB = AF = 4,
在△ADF中,AD = 5,DF = 3,且$3^2 + 4^2 = 5^2$,
∴$FD^2 + AF^2 = AD^2$,
∴△ADF是直角三角形.
(2)由
(1)知,∠AFD = 90°.
设BE = x,则EF = x,
根据折叠可知,∠AFE = ∠B = 90°.
∵∠AFD = 90°,
∴∠DFE = 180°,
∴D,F,E三点在同一条直线上,
∴DE = 3 + x,
CE = 5 - x,DC = AB = 4,
在Rt△DCE中,根据勾股定理,得$DE^2 = DC^2 + EC^2$,
∴$(3 + x)^2 = 4^2 + (5 - x)^2$,解得x = 2.
故BE的长为2.