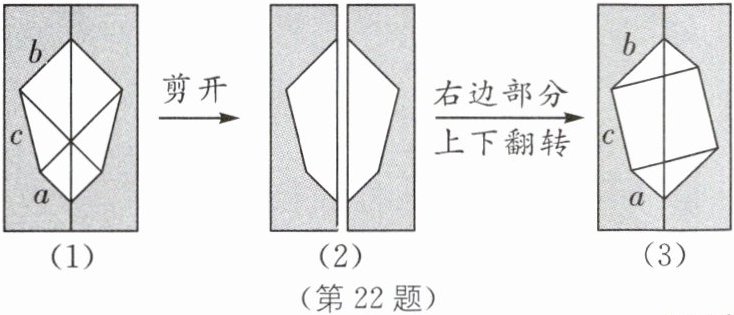
22.(2024·连云港海州区期中)意大利著名画家达·芬奇用如图所示的方法证明了勾股定理,其中图(1)的空白部分由两个正方形和两个直角三角形组成,图(3)的空白部分由两个直角三角形和一个正方形组成. 设图(1)中空白部分的面积为$S_1$,图(3)中空白部分的面积为$S_2$.
(1)请用含a,b,c的代数式分别表示$S_1$,$S_2$;
(2)请利用达·芬奇的方法证明勾股定理.
(1)请用含a,b,c的代数式分别表示$S_1$,$S_2$;
(2)请利用达·芬奇的方法证明勾股定理.

答案:
(1)根据题意,得题图
(1)中空白部分的面积为$S_1 = a^2 + b^2 + 2×\frac{1}{2}ab = a^2 + b^2 + ab$,
题图
(3)中空白部分的面积为$S_2 = c^2 + 2×\frac{1}{2}ab = c^2 + ab$.
(2)由$S_1 = S_2$,得$a^2 + b^2 + ab = c^2 + ab$,
∴$a^2 + b^2 = c^2$.
(1)根据题意,得题图
(1)中空白部分的面积为$S_1 = a^2 + b^2 + 2×\frac{1}{2}ab = a^2 + b^2 + ab$,
题图
(3)中空白部分的面积为$S_2 = c^2 + 2×\frac{1}{2}ab = c^2 + ab$.
(2)由$S_1 = S_2$,得$a^2 + b^2 + ab = c^2 + ab$,
∴$a^2 + b^2 = c^2$.
23.在$\triangle ABC$中,$\angle C= 90^\circ$,$AC= 6$,$BC= 8$,D,E分别是斜边AB和直角边CB上的点,把$\triangle ABC$沿着直线DE折叠,顶点B的对应点是$B'$.
(1)如图(1),如果点$B'$和顶点A重合,求CE的长;
(2)如图(2),如果点$B'$落在AC的中点上,求CE的长.

(1)如图(1),如果点$B'$和顶点A重合,求CE的长;
(2)如图(2),如果点$B'$落在AC的中点上,求CE的长.

答案:
(1)设CE = x,则BE = 8 - x,
由题意,得AE = BE = 8 - x,
在Rt△ACE中,由勾股定理,得$x^2 + 6^2 = (8 - x)^2$,
解得$x = \frac{7}{4}$,即CE的长为$\frac{7}{4}$.
(2)
∵点B'落在AC的中点,
∴$CB' = \frac{1}{2}AC = 3$.
设CE = x,则BE = 8 - x,
由题意,得B'E = BE = 8 - x,
由勾股定理,得$x^2 + 3^2 = (8 - x)^2$,
解得$x = \frac{55}{16}$,即CE的长为$\frac{55}{16}$.
归纳总结 本题主要考查了翻折变换的性质及其应用问题,解题的关键是灵活运用翻折变换的性质,找出图形中隐含的等量关系,借助勾股定理等几何知识来分析、判断、推理或解答.
(1)设CE = x,则BE = 8 - x,
由题意,得AE = BE = 8 - x,
在Rt△ACE中,由勾股定理,得$x^2 + 6^2 = (8 - x)^2$,
解得$x = \frac{7}{4}$,即CE的长为$\frac{7}{4}$.
(2)
∵点B'落在AC的中点,
∴$CB' = \frac{1}{2}AC = 3$.
设CE = x,则BE = 8 - x,
由题意,得B'E = BE = 8 - x,
由勾股定理,得$x^2 + 3^2 = (8 - x)^2$,
解得$x = \frac{55}{16}$,即CE的长为$\frac{55}{16}$.
归纳总结 本题主要考查了翻折变换的性质及其应用问题,解题的关键是灵活运用翻折变换的性质,找出图形中隐含的等量关系,借助勾股定理等几何知识来分析、判断、推理或解答.
24.(2025·盐城建湖期中)综合与实践
[问题驱动]如何验证勾股定理及探究勾股数?
[活动操作]小明参照教材用4张全等的直角三角形纸片拼成如图所示的五边形ABEFG.

[探索新知]
(1)从面积的角度思考,请用两种方法计算五边形ABEFG的面积,并写出得到等式$a^2+b^2= c^2$的过程;
(2)如果满足等式$a^2+b^2= c^2$的a,b,c是三个正整数,我们称a,b,c为勾股数. 已知m,n是正整数且$m>n$,证明:$2mn$,$m^2-n^2$,$m^2+n^2$是勾股数;
[灵活运用]
(3)在如图所示的五边形ABEFG中,若$a= 4$,$b= 8$,则空白部分的面积为______;
(4)请写出任意一组含有85的“勾股数”:______;
(5)小明在他找到的勾股数的表达式中,用$2n^2+4n+4$(n为任意正整数)表示勾股数中的最大的一个数,则另两个数的表达式是______,______.
[问题驱动]如何验证勾股定理及探究勾股数?
[活动操作]小明参照教材用4张全等的直角三角形纸片拼成如图所示的五边形ABEFG.

[探索新知]
(1)从面积的角度思考,请用两种方法计算五边形ABEFG的面积,并写出得到等式$a^2+b^2= c^2$的过程;
如图,延长GM交BE于点D.
方法一:$S_{五边形ABEFG} = S_{正方形ABDN} + S_{正方形MDEF} + S_{\triangle AFG} + S_{\triangle ANG} = b^2 + a^2 + \frac{1}{2}ab + \frac{1}{2}ab = a^2 + b^2 + ab$,
方法二:$S_{五边形ABEFG} = S_{正方形ACFG} + S_{\triangle ABC} + S_{\triangle CEF} = c^2 + \frac{1}{2}ab + \frac{1}{2}ab = c^2 + ab$,
∴$a^2 + b^2 + ab = c^2 + ab$,
∴$a^2 + b^2 = c^2$.
方法一:$S_{五边形ABEFG} = S_{正方形ABDN} + S_{正方形MDEF} + S_{\triangle AFG} + S_{\triangle ANG} = b^2 + a^2 + \frac{1}{2}ab + \frac{1}{2}ab = a^2 + b^2 + ab$,
方法二:$S_{五边形ABEFG} = S_{正方形ACFG} + S_{\triangle ABC} + S_{\triangle CEF} = c^2 + \frac{1}{2}ab + \frac{1}{2}ab = c^2 + ab$,
∴$a^2 + b^2 + ab = c^2 + ab$,
∴$a^2 + b^2 = c^2$.
(2)如果满足等式$a^2+b^2= c^2$的a,b,c是三个正整数,我们称a,b,c为勾股数. 已知m,n是正整数且$m>n$,证明:$2mn$,$m^2-n^2$,$m^2+n^2$是勾股数;
∵$(2mn)^2 = 4m^2n^2$,$(m^2 - n^2)^2 = m^4 + n^4 - 2m^2n^2$,
∴$(2mn)^2 + (m^2 - n^2)^2 = 4m^2n^2 + m^4 + n^4 - 2m^2n^2 = (m^2 + n^2)^2$.
∵m,n是正整数且m>n,
∴2mn,$m^2 - n^2$,$m^2 + n^2$都是正整数,
∴2mn,$m^2 - n^2$,$m^2 + n^2$是勾股数.
∴$(2mn)^2 + (m^2 - n^2)^2 = 4m^2n^2 + m^4 + n^4 - 2m^2n^2 = (m^2 + n^2)^2$.
∵m,n是正整数且m>n,
∴2mn,$m^2 - n^2$,$m^2 + n^2$都是正整数,
∴2mn,$m^2 - n^2$,$m^2 + n^2$是勾股数.
[灵活运用]
(3)在如图所示的五边形ABEFG中,若$a= 4$,$b= 8$,则空白部分的面积为______;
48
(4)请写出任意一组含有85的“勾股数”:______;
85,3612,3613(答案不唯一)
(5)小明在他找到的勾股数的表达式中,用$2n^2+4n+4$(n为任意正整数)表示勾股数中的最大的一个数,则另两个数的表达式是______,______.
$2n^2 + 4n$
$4n + 4$
答案:
(1)如图,延长GM交BE于点D.
方法一:$S_{五边形ABEFG} = S_{正方形ABDN} + S_{正方形MDEF} + S_{\triangle AFG} + S_{\triangle ANG} = b^2 + a^2 + \frac{1}{2}ab + \frac{1}{2}ab = a^2 + b^2 + ab$,
方法二:$S_{五边形ABEFG} = S_{正方形ACFG} + S_{\triangle ABC} + S_{\triangle CEF} = c^2 + \frac{1}{2}ab + \frac{1}{2}ab = c^2 + ab$,
∴$a^2 + b^2 + ab = c^2 + ab$,
∴$a^2 + b^2 = c^2$.
(2)
∵$(2mn)^2 = 4m^2n^2$,$(m^2 - n^2)^2 = m^4 + n^4 - 2m^2n^2$,
∴$(2mn)^2 + (m^2 - n^2)^2 = 4m^2n^2 + m^4 + n^4 - 2m^2n^2 = (m^2 + n^2)^2$.
∵m,n是正整数且m>n,
∴2mn,$m^2 - n^2$,$m^2 + n^2$都是正整数,
∴2mn,$m^2 - n^2$,$m^2 + n^2$是勾股数.
(3)48 [解析]
∵a = 4,b = 8,
∴由
(1)可知,
$S_{五边形ABEFG} = a^2 + b^2 + ab = 4^2 + 8^2 + 4×8 = 112$.
又$S_{\triangle ABC} = \frac{1}{2}ab = \frac{1}{2}×4×8 = 16$,
∴图中空白部分的面积为112 - 4×16 = 48.
(4)85,3612,3613(答案不唯一) [解析]不妨假设$m^2 - n^2 = 85$,m,n是正整数且m>n,
∴(m + n)(m - n) = 85 = 1×85 = 5×17,
$\begin{cases}m + n = 85 \\ m - n = 1 \end{cases}$ 解得$\begin{cases}m = 43 \\ n = 42 \end{cases}$,
∴2mn = 3612,$m^2 + n^2 = 3613$,
∴85,3612,3613是一组勾股数;
$\begin{cases}m + n = 17 \\ m - n = 5 \end{cases}$ 解得$\begin{cases}m = 11 \\ n = 6 \end{cases}$,
∴2mn = 132,$m^2 + n^2 = 157$,
∴85,132,157是一组勾股数.
(5)$2n^2 + 4n$ $4n + 4$ [解析]$(2n^2 + 4n + 4)^2 = 4n^4 + 16n^2 + 16 + 16n^3 + 16n^2 + 32n = (4n^4 + 16n^3 + 16n^2) + (16n^2 + 32n + 16) = (2n^2 + 4n)^2 + (4n + 4)^2$,
∴另两个表达式为$2n^2 + 4n$,$4n + 4$.
(1)如图,延长GM交BE于点D.
方法一:$S_{五边形ABEFG} = S_{正方形ABDN} + S_{正方形MDEF} + S_{\triangle AFG} + S_{\triangle ANG} = b^2 + a^2 + \frac{1}{2}ab + \frac{1}{2}ab = a^2 + b^2 + ab$,
方法二:$S_{五边形ABEFG} = S_{正方形ACFG} + S_{\triangle ABC} + S_{\triangle CEF} = c^2 + \frac{1}{2}ab + \frac{1}{2}ab = c^2 + ab$,
∴$a^2 + b^2 + ab = c^2 + ab$,
∴$a^2 + b^2 = c^2$.
(2)
∵$(2mn)^2 = 4m^2n^2$,$(m^2 - n^2)^2 = m^4 + n^4 - 2m^2n^2$,
∴$(2mn)^2 + (m^2 - n^2)^2 = 4m^2n^2 + m^4 + n^4 - 2m^2n^2 = (m^2 + n^2)^2$.
∵m,n是正整数且m>n,
∴2mn,$m^2 - n^2$,$m^2 + n^2$都是正整数,
∴2mn,$m^2 - n^2$,$m^2 + n^2$是勾股数.
(3)48 [解析]
∵a = 4,b = 8,
∴由
(1)可知,
$S_{五边形ABEFG} = a^2 + b^2 + ab = 4^2 + 8^2 + 4×8 = 112$.
又$S_{\triangle ABC} = \frac{1}{2}ab = \frac{1}{2}×4×8 = 16$,
∴图中空白部分的面积为112 - 4×16 = 48.
(4)85,3612,3613(答案不唯一) [解析]不妨假设$m^2 - n^2 = 85$,m,n是正整数且m>n,
∴(m + n)(m - n) = 85 = 1×85 = 5×17,
$\begin{cases}m + n = 85 \\ m - n = 1 \end{cases}$ 解得$\begin{cases}m = 43 \\ n = 42 \end{cases}$,
∴2mn = 3612,$m^2 + n^2 = 3613$,
∴85,3612,3613是一组勾股数;
$\begin{cases}m + n = 17 \\ m - n = 5 \end{cases}$ 解得$\begin{cases}m = 11 \\ n = 6 \end{cases}$,
∴2mn = 132,$m^2 + n^2 = 157$,
∴85,132,157是一组勾股数.
(5)$2n^2 + 4n$ $4n + 4$ [解析]$(2n^2 + 4n + 4)^2 = 4n^4 + 16n^2 + 16 + 16n^3 + 16n^2 + 32n = (4n^4 + 16n^3 + 16n^2) + (16n^2 + 32n + 16) = (2n^2 + 4n)^2 + (4n + 4)^2$,
∴另两个表达式为$2n^2 + 4n$,$4n + 4$.