25.如图,在数轴上A点表示数a,B点表示数b,C点表示数c,b是最小的正整数,且a,c满足$|a+2|+(c-6)^2= 0$.
(1)$a=$
(2)若将数轴折叠,使得点A与点C重合,则点B与数
(3)点A,B,C开始在数轴上运动,若点A以每秒2个单位长度的速度向左运动,同时,点B和点C分别以每秒1个单位长度和2个单位长度的速度向右运动,假设t秒过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,则$AB=$
(4)在(3)的条件下,请问:是否存在一个常数m,使得$m\cdot BC-AB$不随运动时间t的改变而改变?若存在,请求出m和这个不变化的数值;若不存在,请说明理由.
(1)$a=$
-2
,$b=$1
,$c=$6
.(2)若将数轴折叠,使得点A与点C重合,则点B与数
3
表示的点重合.(3)点A,B,C开始在数轴上运动,若点A以每秒2个单位长度的速度向左运动,同时,点B和点C分别以每秒1个单位长度和2个单位长度的速度向右运动,假设t秒过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,则$AB=$
3t + 3
,$AC=$4t + 8
,$BC=$t + 5
.(用含t的代数式表示)(4)在(3)的条件下,请问:是否存在一个常数m,使得$m\cdot BC-AB$不随运动时间t的改变而改变?若存在,请求出m和这个不变化的数值;若不存在,请说明理由.
存在.理由如下:m·BC - AB = mt + 5m - 3t - 3 = (m - 3)t + 5m - 3,当m = 3时,不变化的数值为12.
答案:
(1) - 2 1 6 [解析]
∵$|a + 2| + (c - 6)^2 = 0$,b是最小的正整数,
∴a = - 2,b = 1,c = 6.
(2)3 [解析]
∵(6 - 2)÷2 = 2,
∴对称点为2,
∴点B表示的数为2×2 - 1 = 3.
(3)3t + 3 4t + 8 t + 5 [解析]AB = 1 + t - (-2 - 2t) = 3t + 3,AC = 6 + 2t - (-2 - 2t) = 4t + 8,BC = 6 + 2t - (1 + t) = t + 5.
(4)存在.理由如下:m·BC - AB = mt + 5m - 3t - 3 = (m - 3)t + 5m - 3,
∴当m = 3时,不变化的数值为12.
(1) - 2 1 6 [解析]
∵$|a + 2| + (c - 6)^2 = 0$,b是最小的正整数,
∴a = - 2,b = 1,c = 6.
(2)3 [解析]
∵(6 - 2)÷2 = 2,
∴对称点为2,
∴点B表示的数为2×2 - 1 = 3.
(3)3t + 3 4t + 8 t + 5 [解析]AB = 1 + t - (-2 - 2t) = 3t + 3,AC = 6 + 2t - (-2 - 2t) = 4t + 8,BC = 6 + 2t - (1 + t) = t + 5.
(4)存在.理由如下:m·BC - AB = mt + 5m - 3t - 3 = (m - 3)t + 5m - 3,
∴当m = 3时,不变化的数值为12.
26.中考新考法 数形结合思想证明等量关系 数形结合是解决数学问题的一种重要的思想方法,借助这种方法可将抽象的数学知识变得直观,从而可以帮助我们快速解题,初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.
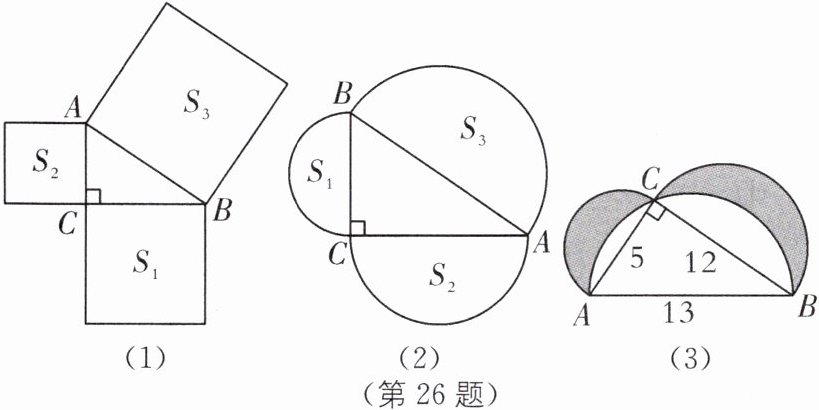
(1)如图(1),在Rt$\triangle ABC$中,$\angle ACB= 90^\circ$,$BC= a$,$AC= b$,$AB= c$,以Rt$\triangle ABC的三边长向外作正方形的面积分别为S_1$,$S_2$,$S_3$,试猜想$S_1$,$S_2$,$S_3$之间存在的等量关系,直接写出结论.
(2)如图(2),如果以Rt$\triangle ABC$的三边长a,b,c为直径向外作半圆,那么第(1)问的结论是否成立?请说明理由.
(3)如图(3),在Rt$\triangle ABC$中,$\angle ACB= 90^\circ$,三边分别为5,12,13,分别以它的三边为直径向上作半圆,求图中阴影部分的面积.

(1)如图(1),在Rt$\triangle ABC$中,$\angle ACB= 90^\circ$,$BC= a$,$AC= b$,$AB= c$,以Rt$\triangle ABC的三边长向外作正方形的面积分别为S_1$,$S_2$,$S_3$,试猜想$S_1$,$S_2$,$S_3$之间存在的等量关系,直接写出结论.
(2)如图(2),如果以Rt$\triangle ABC$的三边长a,b,c为直径向外作半圆,那么第(1)问的结论是否成立?请说明理由.
(3)如图(3),在Rt$\triangle ABC$中,$\angle ACB= 90^\circ$,三边分别为5,12,13,分别以它的三边为直径向上作半圆,求图中阴影部分的面积.
答案:
(1)$S_1 + S_2 = S_3$.
(2)成立.理由如下:
设直角三角形两条直角边分别为a,b,斜边为c,
∴$S_2 = \frac{1}{2}\pi\cdot(\frac{b}{2})^2 = \frac{b^2\pi}{8}$,$S_1 = \frac{1}{2}\pi\cdot(\frac{a}{2})^2 = \frac{a^2\pi}{8}$,
$S_3 = \frac{1}{2}\pi\cdot(\frac{c}{2})^2 = \frac{c^2\pi}{8}$.
∵$\frac{a^2\pi}{8} + \frac{b^2\pi}{8} = \frac{\pi(a^2 + b^2)}{8} = \frac{\pi c^2}{8} = S_3$,
∴$S_1 + S_2 = S_3$.
(3)根据
(2)的结论,两个以直角边为直径的半圆面积等于斜边为直径的半圆面积,故阴影部分的面积 = 两个小半圆的面积
∴阴影部分的面积 = $S_{\triangle ABC}$,
∴阴影部分的面积为5×12÷2 = 30.
(1)$S_1 + S_2 = S_3$.
(2)成立.理由如下:
设直角三角形两条直角边分别为a,b,斜边为c,
∴$S_2 = \frac{1}{2}\pi\cdot(\frac{b}{2})^2 = \frac{b^2\pi}{8}$,$S_1 = \frac{1}{2}\pi\cdot(\frac{a}{2})^2 = \frac{a^2\pi}{8}$,
$S_3 = \frac{1}{2}\pi\cdot(\frac{c}{2})^2 = \frac{c^2\pi}{8}$.
∵$\frac{a^2\pi}{8} + \frac{b^2\pi}{8} = \frac{\pi(a^2 + b^2)}{8} = \frac{\pi c^2}{8} = S_3$,
∴$S_1 + S_2 = S_3$.
(3)根据
(2)的结论,两个以直角边为直径的半圆面积等于斜边为直径的半圆面积,故阴影部分的面积 = 两个小半圆的面积
∴阴影部分的面积 = $S_{\triangle ABC}$,
∴阴影部分的面积为5×12÷2 = 30.