18.(2024·赤峰中考)写出一个比$\sqrt{5}$小的整数
2
.答案:2(答案不唯一) [解析]由于$\sqrt{4}<\sqrt{5}<\sqrt{9}$,即2<$\sqrt{5}$<3,
∴比$\sqrt{5}$小的整数可以是2(答案不唯一).
∴比$\sqrt{5}$小的整数可以是2(答案不唯一).
19.(2024·河北中考)已知a,b,n均为正整数.
(1)若$n<\sqrt{10}<n+1$,则$n= $
(2)若$n-1<\sqrt{a}<n$,$n<\sqrt{b}<n+1$,则满足条件的a的个数总比b的个数少
(1)若$n<\sqrt{10}<n+1$,则$n= $
3
;(2)若$n-1<\sqrt{a}<n$,$n<\sqrt{b}<n+1$,则满足条件的a的个数总比b的个数少
2
个.答案:
(1)3
(2)2 [解析]
(1)
∵$\sqrt{9}<\sqrt{10}<\sqrt{16}$,
∴3<$\sqrt{10}$<4.
∵n<$\sqrt{10}$<n+1,n为正整数,
∴n=3.
(2)
∵n - 1<$\sqrt{a}$<n,
∴$(n - 1)^{2}<a<n^{2}$,
∴a的个数为$n^{2}-(n - 1)^{2}-1=n^{2}-n^{2}+2n - 1 - 1=2n - 2$.
∵n<$\sqrt{b}$<n+1,
∴$n^{2}<b<(n + 1)^{2}$,
∴b的个数为$(n + 1)^{2}-n^{2}-1=n^{2}+2n + 1 - n^{2}-1=2n$.
∵2n-(2n - 2)=2,
∴满足条件的a的个数总比b的个数少2个.
(1)3
(2)2 [解析]
(1)
∵$\sqrt{9}<\sqrt{10}<\sqrt{16}$,
∴3<$\sqrt{10}$<4.
∵n<$\sqrt{10}$<n+1,n为正整数,
∴n=3.
(2)
∵n - 1<$\sqrt{a}$<n,
∴$(n - 1)^{2}<a<n^{2}$,
∴a的个数为$n^{2}-(n - 1)^{2}-1=n^{2}-n^{2}+2n - 1 - 1=2n - 2$.
∵n<$\sqrt{b}$<n+1,
∴$n^{2}<b<(n + 1)^{2}$,
∴b的个数为$(n + 1)^{2}-n^{2}-1=n^{2}+2n + 1 - n^{2}-1=2n$.
∵2n-(2n - 2)=2,
∴满足条件的a的个数总比b的个数少2个.
20.(2024·自贡中考)一次函数$y= (3m+1)x-2$的值随x的增大而增大,请写出一个满足条件的m的值______
1
.答案:1(答案不唯一) [解析]
∵y=(3m + 1)x - 2的值随x的增大而增大,
∴3m + 1>0,
∴$m>-\frac{1}{3}$,
∴m可以为1(答案不唯一).
∵y=(3m + 1)x - 2的值随x的增大而增大,
∴3m + 1>0,
∴$m>-\frac{1}{3}$,
∴m可以为1(答案不唯一).
21.(2024·攀枝花中考)如图,折线OABC表示了距离s(米)与时间t(分)之间的函数关系.
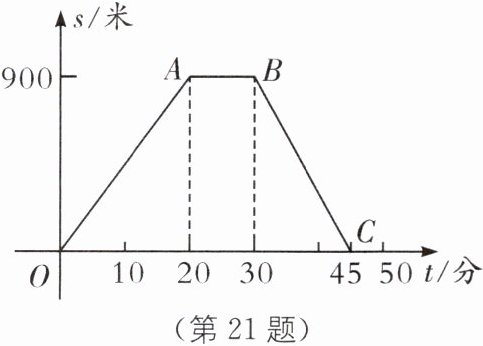
(1)分别直接写出线段OA,AB所对应的函数表达式,并注明相应的t的取值范围;
(2)请你想象一个符合函数图象的实际情境,并用语言进行描述(不必描述具体的速度).

(1)分别直接写出线段OA,AB所对应的函数表达式,并注明相应的t的取值范围;
(2)请你想象一个符合函数图象的实际情境,并用语言进行描述(不必描述具体的速度).
答案:
(1)设线段OA对应的函数表达式为s=kt.
∵点(20,900)在该函数图象上,
∴900=20k,得k=45,
∴线段OA对应的函数表达式为s=45t(0≤t≤20).由图象,可得线段AB对应的函数表达式为s=900(20≤t<30);
(2)小明从家步行去图书馆,图书馆距离小明家900米,用时20分钟,然后小明在图书馆看书用了10分钟,再步行回家,用时15分钟(答案不唯一,符合图象即可).
(1)设线段OA对应的函数表达式为s=kt.
∵点(20,900)在该函数图象上,
∴900=20k,得k=45,
∴线段OA对应的函数表达式为s=45t(0≤t≤20).由图象,可得线段AB对应的函数表达式为s=900(20≤t<30);
(2)小明从家步行去图书馆,图书馆距离小明家900米,用时20分钟,然后小明在图书馆看书用了10分钟,再步行回家,用时15分钟(答案不唯一,符合图象即可).
22.(2024·新疆中考)[探究]
(1)已知$\triangle ABC和\triangle ADE$都是等边三角形.
①如图(1),当点D在BC上时,连接CE.请探究CA,CE和CD之间的数量关系,并说明理由;
②如图(2),当点D在线段BC的延长线上时,连接CE.请再次探究CA,CE和CD之间的数量关系,并说明理由.
[运用]
(2)如图(3),等边三角形ABC中,$AB= 6$,点E在AC上,$CE= 2\sqrt{3}$.点D是直线BC上的动点,连接DE,以DE为边在DE的右侧作等边三角形DEF,连接CF.当$\triangle CEF$为直角三角形时,请直接写出BD的长.

(1)已知$\triangle ABC和\triangle ADE$都是等边三角形.
①如图(1),当点D在BC上时,连接CE.请探究CA,CE和CD之间的数量关系,并说明理由;
②如图(2),当点D在线段BC的延长线上时,连接CE.请再次探究CA,CE和CD之间的数量关系,并说明理由.
[运用]
(2)如图(3),等边三角形ABC中,$AB= 6$,点E在AC上,$CE= 2\sqrt{3}$.点D是直线BC上的动点,连接DE,以DE为边在DE的右侧作等边三角形DEF,连接CF.当$\triangle CEF$为直角三角形时,请直接写出BD的长.

答案:
(1)①CE+CD=CA.理由如下:
∵△ABC和△ADE是等边三角形,
∴AB=AC=BC,AD=AE=DE,∠BAC=∠DAE=60°,
∴∠BAC - ∠DAC=∠DAE - ∠DAC,
∴∠BAD=∠CAE.在△ABD和△ACE中,$\left\{\begin{array}{l} AB=AC,\\ ∠BAD=∠CAE,\\ AD=AE,\end{array}\right. $
∴△ABD≌△ACE(SAS).
∴CE=BD.
∵BD+CD=BC,
∴CE+CD=CA.
②CA+CD=CE.理由如下:
∵△ABC和△ADE是等边三角形,
∴AB=AC=BC,AD=AE=DE,∠BAC=∠DAE=60°,
∴∠BAC + ∠DAC=∠DAE + ∠DAC,
∴∠BAD=∠CAE.在△ABD和△ACE中,$\left\{\begin{array}{l} AB=AC,\\ ∠BAD=∠CAE,\\ AD=AE,\end{array}\right. $
∴△ABD≌△ACE(SAS).
∴CE=BD.
∵CB+CD=BD,
∴CA+CD=CE.
(2)$6 - \sqrt{3}$或$6 + 2\sqrt{3}$
(1)①CE+CD=CA.理由如下:
∵△ABC和△ADE是等边三角形,
∴AB=AC=BC,AD=AE=DE,∠BAC=∠DAE=60°,
∴∠BAC - ∠DAC=∠DAE - ∠DAC,
∴∠BAD=∠CAE.在△ABD和△ACE中,$\left\{\begin{array}{l} AB=AC,\\ ∠BAD=∠CAE,\\ AD=AE,\end{array}\right. $
∴△ABD≌△ACE(SAS).
∴CE=BD.
∵BD+CD=BC,
∴CE+CD=CA.
②CA+CD=CE.理由如下:
∵△ABC和△ADE是等边三角形,
∴AB=AC=BC,AD=AE=DE,∠BAC=∠DAE=60°,
∴∠BAC + ∠DAC=∠DAE + ∠DAC,
∴∠BAD=∠CAE.在△ABD和△ACE中,$\left\{\begin{array}{l} AB=AC,\\ ∠BAD=∠CAE,\\ AD=AE,\end{array}\right. $
∴△ABD≌△ACE(SAS).
∴CE=BD.
∵CB+CD=BD,
∴CA+CD=CE.
(2)$6 - \sqrt{3}$或$6 + 2\sqrt{3}$