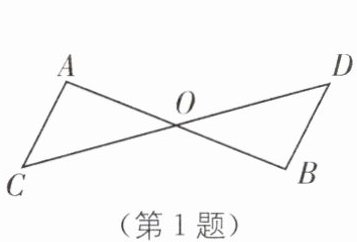
1.(2023·甘孜州中考)如图,AB 与 CD 相交于点 O,AC//BD,只添加一个条件,能判定△AOC≌△BOD 的是(
A.∠A= ∠D
B.AO= BO
C.AC= BO
D.AB= CD
]
B
).
A.∠A= ∠D
B.AO= BO
C.AC= BO
D.AB= CD
]
答案:B
解析:
∵AC//BD,
∴∠A=∠B,∠C=∠D,
∵AB与CD相交于点O,
∴∠AOC=∠BOD,
添加条件AO=BO,
在△AOC和△BOD中,
∠A=∠B,
AO=BO,
∠AOC=∠BOD,
∴△AOC≌△BOD(ASA),
B
2.(2025·无锡宜兴期末)如图,已知 AB//CD,AD//BC,AC 与 BD 交于点 O,AE⊥BD 于点 E,CF⊥BD 于点 F,那么图中全等的三角形有(
A.5对
B.6对
C.7对
D.8对
C
).A.5对
B.6对
C.7对
D.8对
答案:C
解析:
∵AB//CD,AD//BC,
∴四边形ABCD是平行四边形,
∴AD=BC,AB=CD,∠BAD=∠BCD,∠ABC=∠ADC,OA=OC,OB=OD。
1. △ABD≌△CDB(SAS,AB=CD,∠BAD=∠BCD,AD=BC);
2. △ABC≌△CDA(SAS,AB=CD,∠ABC=∠ADC,BC=AD);
3. △AOB≌△COD(SAS,OA=OC,∠AOB=∠COD,OB=OD);
4. △AOD≌△COB(SAS,OA=OC,∠AOD=∠COB,OD=OB);
5. △AOE≌△COF(AAS,∠AOE=∠COF,∠AEO=∠CFO=90°,OA=OC);
6. △ADE≌△CBF(HL,AD=BC,DE=BF,AE=CF);
7. △ABE≌△CDF(HL,AB=CD,BE=DF,AE=CF)。
共有7对全等三角形。
C
证明:在△DEC 和△ABC 中,
$\begin{cases} CD=
∴△DEC≌△ABC(SAS),∴
$\begin{cases} CD=
CA
, \\ ∠DCE=∠ACB
, \\ CE= CB
, \end{cases} $∴△DEC≌△ABC(SAS),∴
DE=AB
.答案:CA ∠DCE=∠ACB CB DE=AB
解析:
证明:在△DEC 和△ABC 中,
$\begin{cases} CD= CA, \\ ∠DCE=∠ACB, \\ CE= CB, \end{cases} $
∴△DEC≌△ABC(SAS),
∴DE=AB.
$\begin{cases} CD= CA, \\ ∠DCE=∠ACB, \\ CE= CB, \end{cases} $
∴△DEC≌△ABC(SAS),
∴DE=AB.
4. 教材 P30 习题 T2·变式 如图,在△ABC 和△DCB 中,∠ACB= ∠DBC,添加一个条件,不能证明△ABC 和△DCB 全等的是(

A.∠ABC= ∠DCB
B.AB= DC
C.AC= DB
D.∠A= ∠D
]
B
).
A.∠ABC= ∠DCB
B.AB= DC
C.AC= DB
D.∠A= ∠D
]
答案:B
5.如图,在△ABC 中,AB= AC,AB>BC,点 D 在边 BC 上,CD= 2BD,点 E,F 在线段 AD 上,∠1= ∠2= ∠BAC,若△ABC 的面积为 21,则△FAC 与△BDE 的面积之和是(

A.6
B.7
C.8
D.9
B
).
A.6
B.7
C.8
D.9
答案:B
解析:
设∠BAC=α,则∠1=∠2=α。
∵∠1=∠BAC,∠ABE=∠ABD,
∴△ABE∽△CBA,
∴∠AEB=∠ACB。
∵AB=AC,
∴∠ABC=∠ACB,
∴∠AEB=∠ABC。
∵∠AEB=∠EDB+∠1,∠ABC=∠EBD+∠ABE,∠1=∠BAC=α,∠ABE=∠ABD,
∴∠EDB=∠EBD,
∴EB=ED。
同理可得FA=FC。
设S△BDE=x,S△FAC=y。
∵CD=2BD,S△ABC=21,
∴S△ABD=7,S△ADC=14。
设S△AEF=m,S△BEF=n,则S△ABD=S△BDE+S△BEF+S△AEF=x+n+m=7,S△ADC=S△FAC+S△FDC= y + (S△ADC - S△AFC)=14,又
∵∠2=∠BAC,可证△AFE∽△ADC,△BED∽△BAD,
∴$\frac{m}{14}=\left(\frac{AF}{AD}\right)^2$,$\frac{x}{7}=\left(\frac{DE}{AD}\right)^2$。
∵FA=FC,EB=ED,
∴S△FAC=S△FAD=y,S△BDE=S△BED=x,
∴S△FAD=y = m + n + x,S△ADC= y + S△FDC=14,S△FDC=14 - y。
又S△ABD= x + n + m=7,S△FAD= m + n + x = y,
∴y=7,x + y=7。
即△FAC与△BDE的面积之和是7。
7
∵∠1=∠BAC,∠ABE=∠ABD,
∴△ABE∽△CBA,
∴∠AEB=∠ACB。
∵AB=AC,
∴∠ABC=∠ACB,
∴∠AEB=∠ABC。
∵∠AEB=∠EDB+∠1,∠ABC=∠EBD+∠ABE,∠1=∠BAC=α,∠ABE=∠ABD,
∴∠EDB=∠EBD,
∴EB=ED。
同理可得FA=FC。
设S△BDE=x,S△FAC=y。
∵CD=2BD,S△ABC=21,
∴S△ABD=7,S△ADC=14。
设S△AEF=m,S△BEF=n,则S△ABD=S△BDE+S△BEF+S△AEF=x+n+m=7,S△ADC=S△FAC+S△FDC= y + (S△ADC - S△AFC)=14,又
∵∠2=∠BAC,可证△AFE∽△ADC,△BED∽△BAD,
∴$\frac{m}{14}=\left(\frac{AF}{AD}\right)^2$,$\frac{x}{7}=\left(\frac{DE}{AD}\right)^2$。
∵FA=FC,EB=ED,
∴S△FAC=S△FAD=y,S△BDE=S△BED=x,
∴S△FAD=y = m + n + x,S△ADC= y + S△FDC=14,S△FDC=14 - y。
又S△ABD= x + n + m=7,S△FAD= m + n + x = y,
∴y=7,x + y=7。
即△FAC与△BDE的面积之和是7。
7
6.(广东广州大学附中自主招生)在△ABC 中,高 AD 和高 BE 所在的直线相交于点 F,且 BF= AC,则∠ABC 的度数为
45°或135°
.答案:45°或135°
解析:
情况一:△ABC为锐角三角形
∵AD、BE为高,
∴∠ADB=∠BEC=90°,∠FBD+∠C=∠CAD+∠C=90°,
∴∠FBD=∠CAD
在△FBD和△CAD中,∠FDB=∠CDA=90°,∠FBD=∠CAD,BF=AC
∴△FBD≌△CAD(AAS),
∴BD=AD
∵∠ADB=90°,
∴∠ABC=45°
情况二:△ABC为钝角三角形
同理可证△FBD≌△CAD(AAS),得BD=AD
∵∠ADB=90°,
∴∠ABD=45°,
∴∠ABC=180°-45°=135°
∠ABC的度数为45°或135°
∵AD、BE为高,
∴∠ADB=∠BEC=90°,∠FBD+∠C=∠CAD+∠C=90°,
∴∠FBD=∠CAD
在△FBD和△CAD中,∠FDB=∠CDA=90°,∠FBD=∠CAD,BF=AC
∴△FBD≌△CAD(AAS),
∴BD=AD
∵∠ADB=90°,
∴∠ABC=45°
情况二:△ABC为钝角三角形
同理可证△FBD≌△CAD(AAS),得BD=AD
∵∠ADB=90°,
∴∠ABD=45°,
∴∠ABC=180°-45°=135°
∠ABC的度数为45°或135°
7.教材 P17 例 2·变式 (2025·淮安期中)如图,在△ABC 和△ADE 中,∠C= ∠E,∠1= ∠2,AC= AE,AD,BC 相交于点 F.
(1)求证:△ABC≌△ADE;
(2)若 AB//DE,∠D= 35°,求∠AFB 的度数.
]

(1)求证:△ABC≌△ADE;
(2)若 AB//DE,∠D= 35°,求∠AFB 的度数.
]

答案:
(1)
∵∠1=∠2,
∴∠1+∠CAD=∠2+∠CAD,
∴∠CAB=∠EAD.在△ABC和△ADE中,$\left\{\begin{array}{l} ∠C=∠E,\\ AC=AE,\\ ∠CAB=∠EAD,\end{array}\right.$
∴△ABC≌△ADE(ASA).
(2)
∵AB//DE,∠D=35°,
∴∠1=∠D=35°,由
(1)可知,∠B=∠D=35°,
∴∠AFB=180°−∠1−∠B=180°−35°−35°=110°.
(1)
∵∠1=∠2,
∴∠1+∠CAD=∠2+∠CAD,
∴∠CAB=∠EAD.在△ABC和△ADE中,$\left\{\begin{array}{l} ∠C=∠E,\\ AC=AE,\\ ∠CAB=∠EAD,\end{array}\right.$
∴△ABC≌△ADE(ASA).
(2)
∵AB//DE,∠D=35°,
∴∠1=∠D=35°,由
(1)可知,∠B=∠D=35°,
∴∠AFB=180°−∠1−∠B=180°−35°−35°=110°.