1.下列条件中,不能判定两个直角三角形全等的是(
A.一个锐角和斜边对应相等
B.两条直角边对应相等
C.两个锐角对应相等
D.斜边和一条直角边对应相等
C
).A.一个锐角和斜边对应相等
B.两条直角边对应相等
C.两个锐角对应相等
D.斜边和一条直角边对应相等
答案:C
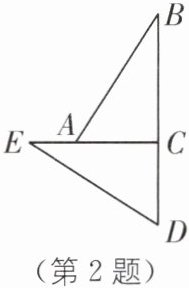
2.(2025·盐城盐都区月考)如图,EC⊥BD,垂足为 C,A 是 EC 上一点,且 AC= CD,AB= DE.若 AC= 3.5,BD= 9,则 AE 的长为(
A.2
B.2.5
C.3
D.5.5
]
A
).
A.2
B.2.5
C.3
D.5.5
]
答案:A
解析:
∵EC⊥BD,
∴∠ACB=∠DCE=90°。
∵AC=CD,AB=DE,
∴Rt△ACB≌Rt△DCE(HL)。
∴BC=CE。
∵AC=3.5,
∴CD=AC=3.5。
∵BD=9,
∴BC=BD - CD=9 - 3.5=5.5。
∴CE=BC=5.5。
∴AE=CE - AC=5.5 - 3.5=2。
A
3.(2025·南京玄武区期中)如图,在△ABC 中,AD⊥BC 于点 D,要使△ABD≌△ACD,若根据“HL”判定,还需要加条件:
AB=AC
.答案:AB=AC
4. 教材 P30 习题 T2·变式 如图,已知∠A= ∠D= 90°,AC= DB.求证:∠ABO= ∠DCO.
]

]

答案:
∵∠A=∠D=90°,
∴△ABC和△DCB是直角三角形.在Rt△ABC和Rt△DCB中,$\left\{\begin{array}{l} AC=DB,\\ BC=CB,\end{array}\right.$
∴Rt△ABC≌Rt△DCB(HL),
∴∠ABC=∠DCB,∠ACB=∠DBC,
∴∠ABC−∠DBC=∠DCB−∠ACB,即∠ABO=∠DCO.
∵∠A=∠D=90°,
∴△ABC和△DCB是直角三角形.在Rt△ABC和Rt△DCB中,$\left\{\begin{array}{l} AC=DB,\\ BC=CB,\end{array}\right.$
∴Rt△ABC≌Rt△DCB(HL),
∴∠ABC=∠DCB,∠ACB=∠DBC,
∴∠ABC−∠DBC=∠DCB−∠ACB,即∠ABO=∠DCO.
5.(2024·苏州吴中区期中)如图,PD⊥AB,PE⊥AC,垂足分别为 D,E,且 PD= PE,则△APD 与△APE 全等的直接理由是(

A.SSS
B.AAS
C.HL
D.ASA
]
C
).
A.SSS
B.AAS
C.HL
D.ASA
]
答案:C
6. 教材 P32 习题 T12·变式 (2025·镇江期中)如图,BE= CF,AE⊥BC,DF⊥BC,要根据“HL”证明 Rt△ABE≌Rt△DCF,则还需要添加一个条件是(

A.AE= DF
B.∠A= ∠D
C.∠B= ∠C
D.AB= DC
D
).
A.AE= DF
B.∠A= ∠D
C.∠B= ∠C
D.AB= DC
答案:D
7.(2024·常州二十四中月考)如图,在 Rt△ABC 中,∠C= 90°,AC= 10,BC= 5,线段 PQ= AB,P,Q 两点分别在 AC 和过点 A 且垂直于 AC 的射线 AO 上运动,则当 AP=
5或10
时,△ABC 和△PQA 全等.答案:5或10
解析:
在Rt△ABC中,∠C=90°,AC=10,BC=5,AO⊥AC,PQ=AB。
情况一:当△ABC≌△QPA时,AP=BC=5;
情况二:当△ABC≌△PQA时,AP=AC=10。
5或10
情况一:当△ABC≌△QPA时,AP=BC=5;
情况二:当△ABC≌△PQA时,AP=AC=10。
5或10
8.实验班原创 如图,点 B,F,C,E 在同一直线上,AC 与 DF 相交于点 G,AB⊥BE,垂足为 B,DE⊥BE,垂足为 E,且 AC= DF,BF= CE.
(1)求证:△ABC≌△DEF;
(2)若∠A= 70°,求∠AGF 的度数.
]

(1)求证:△ABC≌△DEF;
(2)若∠A= 70°,求∠AGF 的度数.
]

答案:
(1)
∵AB⊥BE,
∴∠B=90°.
∵DE⊥BE,
∴∠E=90°.
∵BF=CE,
∴BF+CF=CE+CF,即BC=EF.在Rt△ABC和Rt△DEF中,$\left\{\begin{array}{l} AC=DF,\\ BC=EF,\end{array}\right.$
∴Rt△ABC≌Rt△DEF(HL).
(2)
∵∠A=70°,∠B=90°,
∴∠ACB=90°−70°=20°.由
(1)知,Rt△ABC≌Rt△DEF,
∴∠DFE=∠ACB=20°,
∴∠AGF=∠ACB+∠DFE=40°.
(1)
∵AB⊥BE,
∴∠B=90°.
∵DE⊥BE,
∴∠E=90°.
∵BF=CE,
∴BF+CF=CE+CF,即BC=EF.在Rt△ABC和Rt△DEF中,$\left\{\begin{array}{l} AC=DF,\\ BC=EF,\end{array}\right.$
∴Rt△ABC≌Rt△DEF(HL).
(2)
∵∠A=70°,∠B=90°,
∴∠ACB=90°−70°=20°.由
(1)知,Rt△ABC≌Rt△DEF,
∴∠DFE=∠ACB=20°,
∴∠AGF=∠ACB+∠DFE=40°.