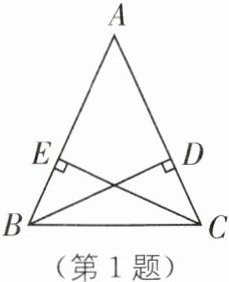
2025年实验班提优训练八年级数学上册苏科版第24页解析答案

1.(2024·连云港期末)如图,在△ABC 中,AB= AC,BD,CE 是高.求证：
(1)△ABD≌△ACE；
(2)BE= CD.

答案：
(1)
∵BD,CE是△ABC的两条高，
∴∠AEC=∠ADB=90°.在△ABD和△ACE中，∠A=∠A，∠ADB=∠AEC，AB=AC，
∴△ABD≌△ACE(AAS).
(2)
∵△ABD≌△ACE，
∴AD=AE.
∵AB=AC，
∴AB - AE=AC - AD，
∴BE=CD.

2. 如图,已知 BE⊥AC,CF⊥AB,BM= AC,CN= AB.求证：AM⊥AN.

答案：
∵BE⊥AC，CF⊥AB，
∴∠B+∠BAC=90°，∠C+∠BAC=90°，
∴∠B=∠C.又BM=CA，AB=NC，
∴△ABM≌△NCA(SAS)，
∴∠BAM=∠N.
∵∠N+∠NAF=90°，
∴∠BAM+∠NAF=90°，即∠MAN=90°，
∴AM⊥AN.

3. 中考新考法猜想探究(2025·扬州宝应期中)如图,已知 AD⊥BC 于点 D,点 E 在 AB 上,CE 交 AD 于点 F,△ABD≌△CFD.
(1)若 BC= 12,AD= 8,求 BD 的长；
(2)试判断 AB 和 CF 的数量关系和位置关系,并说明理由.

答案：
(1)
∵△ABD≌△CFD，
∴BD=DF，AD=DC.
∵BC=12，AD=8，
∴CD=AD=8，
∴BD=BC - CD=12 - 8=4.
(2)AB=CF，且AB⊥CF.理由如下：
∵△ABD≌△CFD，
∴AB=CF，∠BAD=∠FCD.
∵∠AFE=∠CFD，
∴∠AEF=∠CDF=90°，
∴AB⊥CF，
∴AB=CF，且AB⊥CF.

4. 倍长中线模型 (1)如图(1),在△ABC 中,若 AB= 10,AC= 6,则边 BC 上的中线 AD 的取值范围是

2＜AD＜8

；
(2)如图(2),在△ABC 中,D 是边 BC 上的中点,DE⊥DF 于点 D,DE 交 AB 于点 E,DF 交 AC 于点 F,连接 EF,求证：BE+CF＞EF.

如图，延长FD至点G，使DG=DF，连接BG，EG.
∵点D是BC的中点，
∴DB=DC.
∵∠BDG=∠CDF，DG=DF，
∴△BDG≌△CDF(SAS)，
∴BG=CF.
∵ED⊥FD，
∴∠EDF=∠EDG=90°.又ED=ED，FD=GD，
∴△EDF≌△EDG(SAS)，
∴EF=EG.
∵在△BEG中，BE+BG＞EG，在三角形中，任意两边之和大于第三边，
∴BE+CF＞EF.

答案：
(1)2＜AD＜8
(2)如图，延长FD至点G，使DG=DF，连接BG，EG.
∵点D是BC的中点，
∴DB=DC.
∵∠BDG=∠CDF，DG=DF，
∴△BDG≌△CDF(SAS)，
∴BG=CF.
∵ED⊥FD，
∴∠EDF=∠EDG=90°.又ED=ED，FD=GD，
∴△EDF≌△EDG(SAS)，
∴EF=EG.
∵在△BEG中，BE+BG＞EG，在三角形中，任意两边之和大于第三边，
∴BE+CF＞EF.