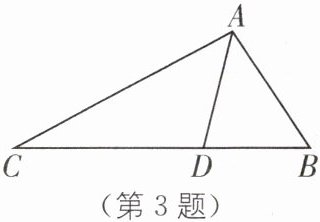
3. 如图,在△ABC中,∠B= 2∠C,AD是∠BAC的平分线.求证:AC= AB+BD.

答案:
3. 如图,在AC上截取AE=AB,连接DE.
∵AD是∠BAC的平分线,
∴∠EAD=∠BAD.
在△AED和△ABD中,
AE=AB,
∠EAD=∠BAD,
AD=AD,
∴△AED≌△ABD(SAS).
∴ED=BD,∠AED=∠B.
∵∠B=2∠C,
∴∠AED=2∠C.
又∠AED为△CED的外角,
∴∠AED=∠C+∠EDC.
∴∠C=∠EDC.
易证EC=ED,在△ECD中,过点E作EH⊥CD,证△ECH≌△EDH,即可得证
∴EC=BD,
∴AC=AE+EC=AB+BD.
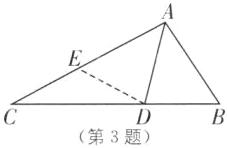
3. 如图,在AC上截取AE=AB,连接DE.
∵AD是∠BAC的平分线,
∴∠EAD=∠BAD.
在△AED和△ABD中,
AE=AB,
∠EAD=∠BAD,
AD=AD,
∴△AED≌△ABD(SAS).
∴ED=BD,∠AED=∠B.
∵∠B=2∠C,
∴∠AED=2∠C.
又∠AED为△CED的外角,
∴∠AED=∠C+∠EDC.
∴∠C=∠EDC.
易证EC=ED,在△ECD中,过点E作EH⊥CD,证△ECH≌△EDH,即可得证
∴EC=BD,
∴AC=AE+EC=AB+BD.

变式3.1 半角模型 (2024·河南开封十四中期中改编)(1)如图(1),在四边形ABCD中,AB= AD,∠B= ∠D= 90°,E,F分别是边BC,CD上的点,且∠EAF= 1/2∠BAD.请直接写出线段EF,BE,FD之间的数量关系:______.
(2)如图(2),在四边形ABCD中,AB= AD,∠B+∠D= 180°,E,F分别是边BC,CD上的点,且∠EAF= 1/2∠BAD,(1)中的结论是否仍然成立?请写出证明过程.
(3)在四边形ABCD中,AB= AD,∠B+∠D= 180°,E,F分别是边BC,CD所在直线上的点,且∠EAF= 1/2∠BAD.请直接写出线段EF,BE,FD之间的数量关系.

(2)如图(2),在四边形ABCD中,AB= AD,∠B+∠D= 180°,E,F分别是边BC,CD上的点,且∠EAF= 1/2∠BAD,(1)中的结论是否仍然成立?请写出证明过程.
(3)在四边形ABCD中,AB= AD,∠B+∠D= 180°,E,F分别是边BC,CD所在直线上的点,且∠EAF= 1/2∠BAD.请直接写出线段EF,BE,FD之间的数量关系.

答案:
变式3.1
(1)EF=BE+FD [解析]如图
(1),延长EB到点G,使BG=DF,连接AG.
在△ABG与△ADF中,AB=AD,∠ABG=∠ADF=90°,BG=DF,
∴△ABG≌△ADF(SAS).
∴AG=AF,∠1=∠2.又∠EAF=$\frac{1}{2}$∠BAD,
∴∠1+∠3=∠2+∠3=$\frac{1}{2}$∠BAD=∠EAF,
∴∠GAE=∠EAF.
又AE=AE,
∴△AEG≌△AEF,
∴EG=EF.
∵EG=BE+BG,
∴EF=BE+FD.

(2)结论仍然成立.证明如下:
如图
(2),延长EB到点G,使得BG=DF,连接AG.
∵∠ABC+∠D=180°,∠ABG+∠ABC=180°,
∴∠ABG=∠D.
在△ABG和△ADF中,
AB=AD,
∠ABG=∠D,
BG=DF,
∴△ABG≌△ADF(SAS),
∴AG=AF,∠1=∠2.
又∠EAF=$\frac{1}{2}$∠BAD,
∴∠1+∠3=∠2+∠3=$\frac{1}{2}$∠BAD=∠EAF,
∴∠GAE=∠EAF.
又AE=AE,
∴△AEG≌△AEF,
∴GE=EF.
∵GE=BE+BG,
∴EF=BE+FD.
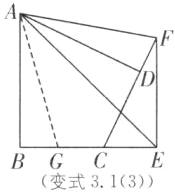
(3)当点E,F分别在BC,CD的延长线上时,如图
(3),在BE上截取BG,使得BG=DF,连接AG.
∵∠B+∠ADC=180°,
∠ADF+∠ADC=180°,
∴∠B=∠ADF.
在△ABG和△ADF中,
AB=AD,
∠ABG=∠ADF,
BG=DF,
∴△ABG≌△ADF(SAS),
∴∠BAG=∠DAF,AG=AF,
∴∠BAG+∠EAD=∠DAF+∠EAD=∠EAF=$\frac{1}{2}$∠BAD,
∴∠GAE=∠EAF.
∵AE=AE,
∴△AEG≌△AEF(SAS),
∴EG=EF.
∵EG=BE - BG,
∴EF=BE - FD.
当点E,F分别在CB,DC的延长线上时,同理可得EG=EF.
∵EG=BG - BE,
∴EF=FD - BE.
当点E,F分别在线段BC,DC上时,由
(2)可知EF=BE+FD.
变式3.1
(1)EF=BE+FD [解析]如图
(1),延长EB到点G,使BG=DF,连接AG.
在△ABG与△ADF中,AB=AD,∠ABG=∠ADF=90°,BG=DF,
∴△ABG≌△ADF(SAS).
∴AG=AF,∠1=∠2.又∠EAF=$\frac{1}{2}$∠BAD,
∴∠1+∠3=∠2+∠3=$\frac{1}{2}$∠BAD=∠EAF,
∴∠GAE=∠EAF.
又AE=AE,
∴△AEG≌△AEF,
∴EG=EF.
∵EG=BE+BG,
∴EF=BE+FD.

(2)结论仍然成立.证明如下:
如图
(2),延长EB到点G,使得BG=DF,连接AG.
∵∠ABC+∠D=180°,∠ABG+∠ABC=180°,
∴∠ABG=∠D.
在△ABG和△ADF中,
AB=AD,
∠ABG=∠D,
BG=DF,
∴△ABG≌△ADF(SAS),
∴AG=AF,∠1=∠2.
又∠EAF=$\frac{1}{2}$∠BAD,
∴∠1+∠3=∠2+∠3=$\frac{1}{2}$∠BAD=∠EAF,
∴∠GAE=∠EAF.
又AE=AE,
∴△AEG≌△AEF,
∴GE=EF.
∵GE=BE+BG,
∴EF=BE+FD.
(3)当点E,F分别在BC,CD的延长线上时,如图
(3),在BE上截取BG,使得BG=DF,连接AG.
∵∠B+∠ADC=180°,
∠ADF+∠ADC=180°,
∴∠B=∠ADF.
在△ABG和△ADF中,
AB=AD,
∠ABG=∠ADF,
BG=DF,
∴△ABG≌△ADF(SAS),
∴∠BAG=∠DAF,AG=AF,
∴∠BAG+∠EAD=∠DAF+∠EAD=∠EAF=$\frac{1}{2}$∠BAD,
∴∠GAE=∠EAF.
∵AE=AE,
∴△AEG≌△AEF(SAS),
∴EG=EF.
∵EG=BE - BG,
∴EF=BE - FD.
当点E,F分别在CB,DC的延长线上时,同理可得EG=EF.
∵EG=BG - BE,
∴EF=FD - BE.
当点E,F分别在线段BC,DC上时,由
(2)可知EF=BE+FD.

4. (2025·北京朝阳区陈经纶中学期中)如图,AD为△ABC中线,点E在AC上,BE交AD于点F,AE= EF,求证:AC= BF.


答案:4. 延长AD到点G,使GD=AD,连接GB,
∵AD为△ABC中线,
∴BD=CD.
在△GBD和△ACD中,
GD=AD,
∠GDB=∠ADC,
BD=CD,
∴△GBD≌△ACD(SAS),
∴GB=AC,∠G=∠CAF.
∵AE=EF,
∴∠CAF=∠EFA,
∴∠G=∠EFA.
∵∠EFA=∠BFG,
∴∠G=∠BFG,
∴GB=BF.
在未学等腰三角形时,可由三角形全等证得
∴AC=BF.
∵AD为△ABC中线,
∴BD=CD.
在△GBD和△ACD中,
GD=AD,
∠GDB=∠ADC,
BD=CD,
∴△GBD≌△ACD(SAS),
∴GB=AC,∠G=∠CAF.
∵AE=EF,
∴∠CAF=∠EFA,
∴∠G=∠EFA.
∵∠EFA=∠BFG,
∴∠G=∠BFG,
∴GB=BF.
在未学等腰三角形时,可由三角形全等证得
∴AC=BF.