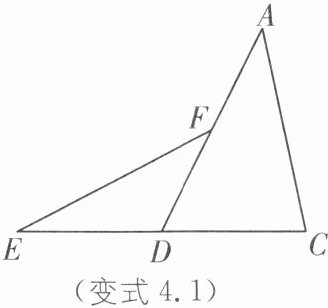
变式4.1 实验班原创 如图,在△ADC中,F为AD的中点,∠DFE= ∠DAC,且EF= AC,若△DEF的面积为2,求△ADC的面积.

答案:
变式4.1 如图,过点C作CM⊥AD于点M,过点E作EN⊥AD的延长线于点N,则∠END=∠CMD=∠CMA=90°.
∵∠DAC=∠DFE,
即∠CAM=∠NFE,
又AC=EF,
∴△ACM≌△FEN,
∴CM=EN.
在△EDN和△CDM中,
∠N=∠CMD=90°,
∠EDN=∠CDM,
EN=CM,
∴△EDN≌△CDM(AAS),
∴ED=CD.
连接CF,则S△CDF=S△EDF=2.
又F为AD的中点,
∴S△ADC=2S△CDF=4.

变式4.1 如图,过点C作CM⊥AD于点M,过点E作EN⊥AD的延长线于点N,则∠END=∠CMD=∠CMA=90°.
∵∠DAC=∠DFE,
即∠CAM=∠NFE,
又AC=EF,
∴△ACM≌△FEN,
∴CM=EN.
在△EDN和△CDM中,
∠N=∠CMD=90°,
∠EDN=∠CDM,
EN=CM,
∴△EDN≌△CDM(AAS),
∴ED=CD.
连接CF,则S△CDF=S△EDF=2.
又F为AD的中点,
∴S△ADC=2S△CDF=4.

变式4.2 (2024·山东临沂河东区期中)如图,在四边形ABCD中,AB//DC,E为BC的中点,连接DE,AE,AE⊥DE.若AB= 6,CD= 4,求AD的长.


答案:
变式4.2 延长DE交AB的延长线于点F,如图.
∵E为BC的中点,
∴BE=CE.
∵AB//DC,
∴∠F=∠CDE.
在△BEF和△CED中,
∠F=∠CDE,
∠BEF=∠CED,
BE=CE,
∴△BEF≌△CED(AAS),
∴EF=DE,BF=CD=4,
∴AF=AB+BF=10.
∵AE⊥DE,
∴∠AED=∠AEF=90°.
又AE=AE,
∴△AEF≌△AED(SAS),
∴AF=AD=10.

变式4.2 延长DE交AB的延长线于点F,如图.
∵E为BC的中点,
∴BE=CE.
∵AB//DC,
∴∠F=∠CDE.
在△BEF和△CED中,
∠F=∠CDE,
∠BEF=∠CED,
BE=CE,
∴△BEF≌△CED(AAS),
∴EF=DE,BF=CD=4,
∴AF=AB+BF=10.
∵AE⊥DE,
∴∠AED=∠AEF=90°.
又AE=AE,
∴△AEF≌△AED(SAS),
∴AF=AD=10.

变式4.3 (2024·上海杨浦区双语学校期中改编)如图,已知AD是△ACB的中线,点E是AC上的一点,BE交AD于点F,AC= BF,∠DAC= 24°,∠EBC= 30°,求∠ACB的度数.


答案:
变式4.3 如图,延长AD到点M,使得DM=AD,连接BM.
在△BDM和△CDA中,
DM=DA,
∠BDM=∠CDA,
BD=CD,
∴△BDM≌△CDA(SAS),
∴BM=AC=BF,∠M=∠DAC=24°,∠ACB=∠DBM,
∴∠M=∠BFM=24°,
∴∠MBF=180° - ∠M - ∠BFM=132°.
∵∠EBC=30°,
∴∠DBM=∠MBF - ∠EBC=102°,
∴∠ACB=∠DBM=102°.

变式4.3 如图,延长AD到点M,使得DM=AD,连接BM.
在△BDM和△CDA中,
DM=DA,
∠BDM=∠CDA,
BD=CD,
∴△BDM≌△CDA(SAS),
∴BM=AC=BF,∠M=∠DAC=24°,∠ACB=∠DBM,
∴∠M=∠BFM=24°,
∴∠MBF=180° - ∠M - ∠BFM=132°.
∵∠EBC=30°,
∴∠DBM=∠MBF - ∠EBC=102°,
∴∠ACB=∠DBM=102°.

变式4.4 (2025·山东德州乐陵期中)(1)[旧题重现]《学习与评价》P19有这样一道习题:
如图(1),AD,A'D'分别是△ABC和△A'B'C'的BC,B'C'边上的中线,AD= A'D',AB= A'B',BC= B'C'.求证:△ABC≌△A'B'C'.
证明的途径可以用下面的框图表示,请填写其中的空格.
$\boxed{AD是△ABC的中线}$→$\boxed{①}$→$\boxed{③}$
$\boxed{AD'是△A'B'C'的中线}$→$\boxed{②}$→$\boxed{BD= B'D'}$→$\boxed{△ABD≌△A'B'D'}$
$\boxed{BC= B'C'}$→$\boxed{AB= A'B'}$→$\boxed{④}$
$\boxed{△ABC≌△A'B'C'}$

(2)[深入研究]
如图(2),AD,A'D'分别是△ABC和△A'B'C'的BC,B'C'边上的中线,AD= A'D',AB= A'B',AC= A'C'.判断△ABC与△A'B'C'是否仍然全等,并说明理由.


如图(1),AD,A'D'分别是△ABC和△A'B'C'的BC,B'C'边上的中线,AD= A'D',AB= A'B',BC= B'C'.求证:△ABC≌△A'B'C'.
证明的途径可以用下面的框图表示,请填写其中的空格.
$\boxed{AD是△ABC的中线}$→$\boxed{①}$→$\boxed{③}$
$\boxed{AD'是△A'B'C'的中线}$→$\boxed{②}$→$\boxed{BD= B'D'}$→$\boxed{△ABD≌△A'B'D'}$
$\boxed{BC= B'C'}$→$\boxed{AB= A'B'}$→$\boxed{④}$
$\boxed{△ABC≌△A'B'C'}$

(2)[深入研究]
如图(2),AD,A'D'分别是△ABC和△A'B'C'的BC,B'C'边上的中线,AD= A'D',AB= A'B',AC= A'C'.判断△ABC与△A'B'C'是否仍然全等,并说明理由.


答案:
变式4.4
(1)
∵AD是△ABC的中线,
∴BD=$\frac{1}{2}$BC.
∵A'D'是△A'B'C'的中线,
∴B'D'=$\frac{1}{2}$B'C'.
∵BC=B'C',
∴BD=B'D'.
在△ABD和△A'B'D'中,
BD=B'D',
AD=A'D',
AB=A'B',
∴△ABD≌△A'B'D'(SSS),
∴∠B=∠B'.
在△ABC和△A'B'C'中,
AB=A'B',
∠B=∠B',
BC=B'C',
∴△ABC≌△A'B'C'(SAS).
(2)△ABC和△A'B'C'仍然全等.理由如下:
如图,延长AD至E,使DE=AD,连接BE,延长A'D'至E',使D'E'=A'D',连接B'E'.
∵AD和A'D'分别是△ABC和△A'B'C'的BC和B'C'边上的中线,
∴BD=CD,B'D'=C'D'.
在△ADC和△EDB中,
AD=DE,
∠ADC=∠BDE,
CD=BD,
∴△ADC≌△EDB(SAS),
∴AC=EB,∠DAC=∠E.
同理A'C'=E'B',∠D'A'C'=∠E'.
∵AC=A'C',
∴EB=E'B'.
∵AD=A'D',AD=DE,A'D'=D'E',
∴AE=A'E'.
∵AB=A'B',
∴△ABE≌△A'B'E'(SSS),
∴∠BAE=∠B'A'E',∠E=∠E',
∴∠DAC=∠D'A'C',
∴∠BAC=∠B'A'C'.
又AB=A'B',AC=A'C',
∴△ABC≌△A'B'C'(SAS).

变式4.4
(1)
∵AD是△ABC的中线,
∴BD=$\frac{1}{2}$BC.
∵A'D'是△A'B'C'的中线,
∴B'D'=$\frac{1}{2}$B'C'.
∵BC=B'C',
∴BD=B'D'.
在△ABD和△A'B'D'中,
BD=B'D',
AD=A'D',
AB=A'B',
∴△ABD≌△A'B'D'(SSS),
∴∠B=∠B'.
在△ABC和△A'B'C'中,
AB=A'B',
∠B=∠B',
BC=B'C',
∴△ABC≌△A'B'C'(SAS).
(2)△ABC和△A'B'C'仍然全等.理由如下:
如图,延长AD至E,使DE=AD,连接BE,延长A'D'至E',使D'E'=A'D',连接B'E'.
∵AD和A'D'分别是△ABC和△A'B'C'的BC和B'C'边上的中线,
∴BD=CD,B'D'=C'D'.
在△ADC和△EDB中,
AD=DE,
∠ADC=∠BDE,
CD=BD,
∴△ADC≌△EDB(SAS),
∴AC=EB,∠DAC=∠E.
同理A'C'=E'B',∠D'A'C'=∠E'.
∵AC=A'C',
∴EB=E'B'.
∵AD=A'D',AD=DE,A'D'=D'E',
∴AE=A'E'.
∵AB=A'B',
∴△ABE≌△A'B'E'(SSS),
∴∠BAE=∠B'A'E',∠E=∠E',
∴∠DAC=∠D'A'C',
∴∠BAC=∠B'A'C'.
又AB=A'B',AC=A'C',
∴△ABC≌△A'B'C'(SAS).
