1. 教材 P44 练习 T1·变式(2023·宿迁中考)若等腰三角形有一个内角为$110^\circ$,则这个等腰三角形的底角是(
A.$70^\circ$
B.$45^\circ$
C.$35^\circ$
D.$50^\circ$
C
).A.$70^\circ$
B.$45^\circ$
C.$35^\circ$
D.$50^\circ$
答案:1.C [解析]当等腰三角形的顶角为110°时,则它的底角度数为$\frac{180^\circ - 110^\circ}{2}=35^\circ$.故选C.
归纳总结 本题考查了等腰三角形的性质、三角形内角和定理,熟练掌握等腰三角形的性质,以及三角形内角和定理是解题的关键.
归纳总结 本题考查了等腰三角形的性质、三角形内角和定理,熟练掌握等腰三角形的性质,以及三角形内角和定理是解题的关键.
2. 教材 P49 习题 T1·变式 已知等腰三角形的周长为 21,其中一边长为 5,则该等腰三角形的底边长是(
A.5
B.8
C.11
D.5 或 11
A
).A.5
B.8
C.11
D.5 或 11
答案:2.A [解析]当腰长为5时,底边长为21 - 2×5 = 11,三角形的三边长为5,5,11,不能构成三角形;当底边长为5时,腰长为(21 - 5)÷2 = 8,三角形的三边长为8,8,5,能构成等腰三角形.所以等腰三角形的底边长为5.故选A.
易错警示 本题考查了等腰三角形的性质和三角形的三边关系.已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形,再进行解答,这点非常重要,也是解题的关键
易错警示 本题考查了等腰三角形的性质和三角形的三边关系.已知没有明确腰和底边的题目一定要想到两种情况,分类进行讨论,还应验证各种情况是否能构成三角形,再进行解答,这点非常重要,也是解题的关键
3. (2025·无锡江阴期中)等腰三角形的两边长分别是 3 和 6,那么这个三角形的周长是
15
.答案:3.15 [解析]①若3为腰长,6为底边长,由于3 + 3 = 6,则三角形不存在;
②若6为腰长,则符合三角形的两边之和大于第三边,
所以这个三角形的周长为6 + 6 + 3 = 15.
②若6为腰长,则符合三角形的两边之和大于第三边,
所以这个三角形的周长为6 + 6 + 3 = 15.
4. 如图,在$\triangle ABC$中,$AB= AC$,过$BC的中点D作DE \perp AB$,$DF \perp AC$,垂足分别为$E$,$F$. 若$\angle BDE= 40^\circ$,求$\angle BAC$的度数.
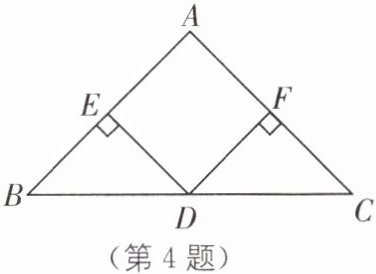

答案:4.
∵∠BDE = 40°,
∴∠B = 90° - ∠BDE = 50°,
∴∠C = 50°,
∴∠BAC = 180° - ∠B - ∠C = 80°.
∵∠BDE = 40°,
∴∠B = 90° - ∠BDE = 50°,
∴∠C = 50°,
∴∠BAC = 180° - ∠B - ∠C = 80°.
5. 教材 P44 例 2·变式(2025·苏州张家港二中期中)如图,在$\triangle ABC$中,点$D$,$E分别在边AB$,$AC$上,$DE // BC$,$EB平分\angle DEC$.
(1)求证:$BC= CE$;
(2)若$CE= AB$,$EA= EB$,求$\angle C$的度数.

(1)求证:$BC= CE$;
(2)若$CE= AB$,$EA= EB$,求$\angle C$的度数.

答案:5.
(1)
∵EB平分∠DEC,
∴∠DEB = ∠BEC.
∵DE//BC,
∴∠DEB = ∠EBC,
∴∠BEC = ∠EBC,
∴BC = CE.
(2)
∵BC = CE,CE = AB,
∴BC = AB,
∴∠C = ∠A.
设∠C = ∠A = x,
∵EA = EB,
∴∠ABE = ∠A = x,
∴∠EBC = ∠BEC = ∠A + ∠ABE = 2x,
∴2x + 2x + x = 180°,
∴∠C = x = 36°.
(1)
∵EB平分∠DEC,
∴∠DEB = ∠BEC.
∵DE//BC,
∴∠DEB = ∠EBC,
∴∠BEC = ∠EBC,
∴BC = CE.
(2)
∵BC = CE,CE = AB,
∴BC = AB,
∴∠C = ∠A.
设∠C = ∠A = x,
∵EA = EB,
∴∠ABE = ∠A = x,
∴∠EBC = ∠BEC = ∠A + ∠ABE = 2x,
∴2x + 2x + x = 180°,
∴∠C = x = 36°.
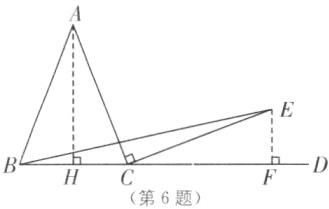
6. (2024·苏州期中)如图,在等腰三角形$ABC$中,$AB= AC$,$D为BC$延长线上一点,$EC \perp AC且AC= CE$,垂足为$C$,连接$BE$,若$BC= 6$,则$\triangle BCE$的面积为( ).

A.$\frac{9}{2}$
B.9
C.18
D.36

A.$\frac{9}{2}$
B.9
C.18
D.36
答案:
6.B [解析]如图,过点A作AH⊥BC于点H,过点E作EF⊥BC于点F.
在△ABC中,
∵AB = AC,
∴BH = HC.
∵∠ACE = 90°,
∴∠ACH + ∠ECF = 90°.
∵∠CAH + ∠ACH = 90°,
∴∠ECF = ∠CAH.
在△ACH与△CEF中,∠AHC = ∠CFE = 90°,∠CAH = ∠ECF,AC = CE,
∴△ACH≌△CEF(AAS),
∴EF = CH = $\frac{1}{2}$BC = 3,
∴△BCE的面积 = $\frac{1}{2}$BC·EF = $\frac{1}{2}$×6×3 = 9.
故选B
6.B [解析]如图,过点A作AH⊥BC于点H,过点E作EF⊥BC于点F.
在△ABC中,
∵AB = AC,
∴BH = HC.
∵∠ACE = 90°,
∴∠ACH + ∠ECF = 90°.
∵∠CAH + ∠ACH = 90°,
∴∠ECF = ∠CAH.
在△ACH与△CEF中,∠AHC = ∠CFE = 90°,∠CAH = ∠ECF,AC = CE,
∴△ACH≌△CEF(AAS),
∴EF = CH = $\frac{1}{2}$BC = 3,
∴△BCE的面积 = $\frac{1}{2}$BC·EF = $\frac{1}{2}$×6×3 = 9.
故选B

7. (连云港宁海中学自主招生)如图,$\triangle ABC的三条高相交于点G$,$CH$是角平分线,已知$\angle ABC= 45^\circ$,$\angle ACD= 60^\circ$,则图中的等腰三角形共有(

A.5 个
B.6 个
C.7 个
D.8 个
D
).
A.5 个
B.6 个
C.7 个
D.8 个
答案:7.D [解析]①
∵AD⊥BC,∠ABC = 45°,
∴△ABD是等腰三角形;
②
∵CF⊥AB,∠ABC = 45°,
∴△BCF是等腰三角形;
③
∵∠ACB = 60°,
∴∠CBE = 90° - 60° = 30°.
∵CH是角平分线,
∴∠BCH = ∠ACH = $\frac{1}{2}$∠ACB = 30°,
∴∠CBI = ∠ICB,
∴△BCI是等腰三角形;
④
∵∠ACB = 60°,
∴∠CAD = 90° - 60° = 30°,
∴∠ACJ = ∠CAJ = 30°,
∴△ACJ是等腰三角形;
⑤
∵∠ACF = 60° - 45° = 15°,
∴∠CAF = 90° - 15° = 75°,
∵∠AHC = ∠ABC + ∠BCH = 45° + 30° = 75°,
∴∠CAH = ∠CHA = 75°,
∴△ACH是等腰三角形;
⑥
∵∠GCD = ∠DGC = 45°,
∴△CDG是等腰三角形;
⑦
∵∠GIJ = ∠EBC + ∠HCB = 30° + 30° = 60°,
∠GJI = ∠CJD = 90° - 30° = 60°,
∴∠GIJ = ∠GJI = 60°,
∴△GIJ是等腰三角形;
⑧△AFG是等腰三角形.
综上分析,题图中等腰三角形共有8个:△ABD,△BCF,△BCI,△ACJ,△ACH,△CDG,△GIJ,△AFG.故选D
∵AD⊥BC,∠ABC = 45°,
∴△ABD是等腰三角形;
②
∵CF⊥AB,∠ABC = 45°,
∴△BCF是等腰三角形;
③
∵∠ACB = 60°,
∴∠CBE = 90° - 60° = 30°.
∵CH是角平分线,
∴∠BCH = ∠ACH = $\frac{1}{2}$∠ACB = 30°,
∴∠CBI = ∠ICB,
∴△BCI是等腰三角形;
④
∵∠ACB = 60°,
∴∠CAD = 90° - 60° = 30°,
∴∠ACJ = ∠CAJ = 30°,
∴△ACJ是等腰三角形;
⑤
∵∠ACF = 60° - 45° = 15°,
∴∠CAF = 90° - 15° = 75°,
∵∠AHC = ∠ABC + ∠BCH = 45° + 30° = 75°,
∴∠CAH = ∠CHA = 75°,
∴△ACH是等腰三角形;
⑥
∵∠GCD = ∠DGC = 45°,
∴△CDG是等腰三角形;
⑦
∵∠GIJ = ∠EBC + ∠HCB = 30° + 30° = 60°,
∠GJI = ∠CJD = 90° - 30° = 60°,
∴∠GIJ = ∠GJI = 60°,
∴△GIJ是等腰三角形;
⑧△AFG是等腰三角形.
综上分析,题图中等腰三角形共有8个:△ABD,△BCF,△BCI,△ACJ,△ACH,△CDG,△GIJ,△AFG.故选D
8. (2023·锦州中考)如图,在$\triangle ABC$中,$BC的垂直平分线交BC于点D$,交$AB于点E$,连接$CE$. 若$CE= CA$,$\angle ACE= 40^\circ$,则$\angle B$的度数为______

35°
.
答案:8.35° [解析]
∵CE = AC,
∴∠A = ∠AEC.
∵∠A + ∠AEC + ∠ACE = 180°,∠ACE = 40°,
∴∠AEC = $\frac{1}{2}$×(180° - 40°) = 70°.
∵DE是BC的垂直平分线,
∴BE = CE,
∴∠B = ∠BCE.
∵∠AEC = ∠B + ∠BCE,
∴∠B = $\frac{1}{2}$∠AEC = 35°.
∵CE = AC,
∴∠A = ∠AEC.
∵∠A + ∠AEC + ∠ACE = 180°,∠ACE = 40°,
∴∠AEC = $\frac{1}{2}$×(180° - 40°) = 70°.
∵DE是BC的垂直平分线,
∴BE = CE,
∴∠B = ∠BCE.
∵∠AEC = ∠B + ∠BCE,
∴∠B = $\frac{1}{2}$∠AEC = 35°.
9. (南师附中特长生)如图,在$\triangle ABC$中,$AB= AC$,$AD= AE$,$\angle BAD= 40^\circ$,则$\angle EDC= $
20°
.答案:9.20° [解析]因为AB = AC,所以∠B = ∠C.
设∠EDC = x,∠B = ∠C = y,
则∠AED = ∠EDC + ∠C = x + y,
因为AD = AE,所以∠ADE = ∠AED = x + y,
所以∠ADC = ∠ADE + ∠EDC = 2x + y.
又∠ADC = ∠B + ∠BAD,
所以2x + y = y + 40,解得x = 20°,
所以∠EDC的度数是20°.
设∠EDC = x,∠B = ∠C = y,
则∠AED = ∠EDC + ∠C = x + y,
因为AD = AE,所以∠ADE = ∠AED = x + y,
所以∠ADC = ∠ADE + ∠EDC = 2x + y.
又∠ADC = ∠B + ∠BAD,
所以2x + y = y + 40,解得x = 20°,
所以∠EDC的度数是20°.
10. 过等腰三角形顶角顶点的一条直线,将该等腰三角形分成的两个三角形均为等腰三角形,则原等腰三角形的底角度数为______.
答案:
10.36°或45° [解析]分两种情况讨论:
①如图
(1),在△ABC中,AB = AC,BD = AD,AC = CD,
∴∠B = ∠C = ∠BAD,∠CDA = ∠CAD,
∵∠CDA = ∠B + ∠BAD = 2∠B,
∴∠CAB = ∠CAD + ∠BAD = 3∠B.
∵∠BAC + ∠B + ∠C = 180°,
∴5∠B = 180°,
∴∠B = 36°.
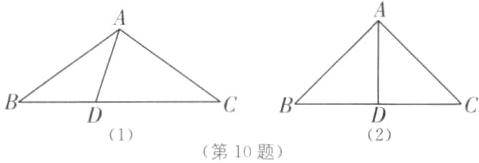
②如图
(2),在△ABC中,AB = AC,AD = BD = CD,
∴∠B = ∠C = ∠DAC = ∠DAB,
∴∠BAC = 2∠B.
∵∠BAC + ∠B + ∠C = 180°,
∴4∠B = 180°,
∴∠B = 45°.
10.36°或45° [解析]分两种情况讨论:
①如图
(1),在△ABC中,AB = AC,BD = AD,AC = CD,
∴∠B = ∠C = ∠BAD,∠CDA = ∠CAD,
∵∠CDA = ∠B + ∠BAD = 2∠B,
∴∠CAB = ∠CAD + ∠BAD = 3∠B.
∵∠BAC + ∠B + ∠C = 180°,
∴5∠B = 180°,
∴∠B = 36°.

②如图
(2),在△ABC中,AB = AC,AD = BD = CD,
∴∠B = ∠C = ∠DAC = ∠DAB,
∴∠BAC = 2∠B.
∵∠BAC + ∠B + ∠C = 180°,
∴4∠B = 180°,
∴∠B = 45°.