9.(2024·苏州蠡口中学月考)如图,在△ABC 中,AD 为 BC 边上的高,AE 是∠BAD 的平分线,点 F 为 AE 上一点,连接 BF,$\angle BFE= 45^\circ$.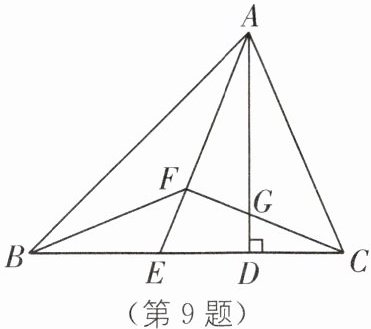
(1)求证:BF 平分∠ABE;
(2)连接 CF 交 AD 于点 G,若$S_{\triangle ABF}= S_{\triangle CBF}$,求证:$\angle AFC= 90^\circ$;
(3)在(2)的条件下,当 BE= 3,AG= 4.5 时,求线段 AB 的长.

(1)求证:BF 平分∠ABE;
(2)连接 CF 交 AD 于点 G,若$S_{\triangle ABF}= S_{\triangle CBF}$,求证:$\angle AFC= 90^\circ$;
(3)在(2)的条件下,当 BE= 3,AG= 4.5 时,求线段 AB 的长.
答案:
(1)
∵AE是∠BAD的平分线,
∴∠BAD=2∠BAF.
∵∠BFE=45°,
∴∠FBA+∠BAF=45°,
∴2∠FBA+2∠BAF=90°.
∵AD为BC边上的高,
∴∠EBF+∠FBA+2∠BAF=90°,
∴2∠FBA=∠EBF+∠FBA,
∴∠EBF=∠FBA,
∴BF平分∠ABE.
(2)如图,过点F作FM⊥BC于点M,FN⊥AB于点N.
∵BF平分∠ABE,FM⊥BC,FN⊥AB,
∴FM=FN.
∵${S}_{\triangle ABF}={S}_{\triangle CBF}$,即AB·FN=BC·FM,
∴AB=BC.在△ABF和△CBF中,$\left\{\begin{array}{l}AB=CB,\\ \angle FBA=\angle FBC,\\ BF=BF,\end{array}\right.$
∴△ABF≌△CBF(SAS),
∴∠AFB=∠CFB.
∵∠BFE=45°,
∴∠AFB=180°−45°=135°,
∴∠CFB=135°,
∴∠CFE=∠CFB−∠BFE=135°−45°=90°,
∴∠AFC=180°−90°=90°.
(3)
∵△ABF≌△CBF,
∴AF=FC.
∵∠AFC=∠ADC=90°,∠AGF=∠CGD,
∴∠FAG=∠FCE.在△AFG和△CFE中,$\left\{\begin{array}{l}\angle FAG=\angle FCE,\\ AF=CF,\\ \angle AFG=\angle CFE,\end{array}\right.$
∴△AFG≌△CFE(ASA),
∴AG=EC=4.5.
∵BE=3,
∴BC=BE+EC=7.5,又△ABF≌△CBF,
∴AB=BC=7.5.
(1)
∵AE是∠BAD的平分线,
∴∠BAD=2∠BAF.
∵∠BFE=45°,
∴∠FBA+∠BAF=45°,
∴2∠FBA+2∠BAF=90°.
∵AD为BC边上的高,
∴∠EBF+∠FBA+2∠BAF=90°,
∴2∠FBA=∠EBF+∠FBA,
∴∠EBF=∠FBA,
∴BF平分∠ABE.
(2)如图,过点F作FM⊥BC于点M,FN⊥AB于点N.
∵BF平分∠ABE,FM⊥BC,FN⊥AB,
∴FM=FN.
∵${S}_{\triangle ABF}={S}_{\triangle CBF}$,即AB·FN=BC·FM,
∴AB=BC.在△ABF和△CBF中,$\left\{\begin{array}{l}AB=CB,\\ \angle FBA=\angle FBC,\\ BF=BF,\end{array}\right.$
∴△ABF≌△CBF(SAS),
∴∠AFB=∠CFB.
∵∠BFE=45°,
∴∠AFB=180°−45°=135°,
∴∠CFB=135°,
∴∠CFE=∠CFB−∠BFE=135°−45°=90°,
∴∠AFC=180°−90°=90°.
(3)
∵△ABF≌△CBF,
∴AF=FC.
∵∠AFC=∠ADC=90°,∠AGF=∠CGD,
∴∠FAG=∠FCE.在△AFG和△CFE中,$\left\{\begin{array}{l}\angle FAG=\angle FCE,\\ AF=CF,\\ \angle AFG=\angle CFE,\end{array}\right.$
∴△AFG≌△CFE(ASA),
∴AG=EC=4.5.
∵BE=3,
∴BC=BE+EC=7.5,又△ABF≌△CBF,
∴AB=BC=7.5.
10. 中考新考法 动点问题 如图(1),直线 m 与直线 n 相交于点 O,A,B 两点同时从点 O 出发,点 A 以每秒 x 个单位长度沿直线 n 向左运动,点 B 以每秒 y 个单位长度沿直线 m 向上运动.
(1)若运动 1 s 时,点 B 比点 A 多运动 1 个单位;运动 2 s 时,点 B 与点 A 运动的路程和为 6 个单位,则 x= ______
(2)如图(2),当直线 m 与直线 n 垂直时,设∠BAO 和∠ABO 的平分线相交于点 P. 在点 A,B 运动的过程中,∠APB 的大小是否会发生变化?若不发生变化,请求出其值(写出过程);若发生变化,请说明理由.
不变化,∠APB=135°.
∵直线m⊥直线n,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°.
∵AP平分∠BAO,BP平分∠ABO,
∴∠PAB+∠PBA=$\frac{1}{2}(\angle OAB+\angle ABO)=\frac{1}{2}× 90°=45°$,
∴∠APB=180°−45°=135°.
(3)如图(3),将(2)中的直线 n 不动,直线 m 绕点 O 按顺时针方向旋转$\alpha(0^\circ<\alpha<90^\circ)$,其他条件不变.
(i)用含有α的式子表示∠APB 的度数;
∠APB=135°+$\frac{1}{2}\alpha$.
理由如下:根据题意,得∠AOB=90°+α,
∴∠OAB+∠OBA=180°−∠AOB=90°−α.
∵AP平分∠BAO,BP平分∠ABO,
∴∠PAB+∠PBA=$\frac{1}{2}(\angle OAB+\angle OBA)=45°−\frac{1}{2}\alpha$,
∴∠APB=180°−$(45°−\frac{1}{2}\alpha )$=135°+$\frac{1}{2}\alpha$.
(ii)如果再分别作△ABO 的两个外角∠BAC,∠ABD 的平分线相交于点 Q,并延长 BP,QA 交于点 M. 则下列结论为定值的选项是______
①∠Q+∠M;②∠M-∠Q;③∠APB+∠Q;④∠APB-∠M.
(1)若运动 1 s 时,点 B 比点 A 多运动 1 个单位;运动 2 s 时,点 B 与点 A 运动的路程和为 6 个单位,则 x= ______
1
______,y= ______2
______.(2)如图(2),当直线 m 与直线 n 垂直时,设∠BAO 和∠ABO 的平分线相交于点 P. 在点 A,B 运动的过程中,∠APB 的大小是否会发生变化?若不发生变化,请求出其值(写出过程);若发生变化,请说明理由.
不变化,∠APB=135°.
∵直线m⊥直线n,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°.
∵AP平分∠BAO,BP平分∠ABO,
∴∠PAB+∠PBA=$\frac{1}{2}(\angle OAB+\angle ABO)=\frac{1}{2}× 90°=45°$,
∴∠APB=180°−45°=135°.
(3)如图(3),将(2)中的直线 n 不动,直线 m 绕点 O 按顺时针方向旋转$\alpha(0^\circ<\alpha<90^\circ)$,其他条件不变.
(i)用含有α的式子表示∠APB 的度数;
∠APB=135°+$\frac{1}{2}\alpha$.
理由如下:根据题意,得∠AOB=90°+α,
∴∠OAB+∠OBA=180°−∠AOB=90°−α.
∵AP平分∠BAO,BP平分∠ABO,
∴∠PAB+∠PBA=$\frac{1}{2}(\angle OAB+\angle OBA)=45°−\frac{1}{2}\alpha$,
∴∠APB=180°−$(45°−\frac{1}{2}\alpha )$=135°+$\frac{1}{2}\alpha$.
(ii)如果再分别作△ABO 的两个外角∠BAC,∠ABD 的平分线相交于点 Q,并延长 BP,QA 交于点 M. 则下列结论为定值的选项是______
①③④
______(填序号).①∠Q+∠M;②∠M-∠Q;③∠APB+∠Q;④∠APB-∠M.
答案:
(1)1 2 [解析]由题意,得$\left\{\begin{array}{l}y - x = 1,\\ 2y + 2x = 6,\end{array}\right.$解得$\left\{\begin{array}{l}x = 1,\\ y = 2.\end{array}\right.$
(2)不变化,∠APB=135°.如图
(1),
∵直线m⊥直线n,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°.
∵AP平分∠BAO,BP平分∠ABO,
∴∠PAB+∠PBA=$\frac{1}{2}(\angle OAB+\angle ABO)=\frac{1}{2}× 90°=45°$,
∴∠APB=180°−45°=135°.
(3)(i)∠APB=135°+$\frac{1}{2}\alpha$.理由如下:根据题意,得∠AOB=90°+α,
∴∠OAB+∠OBA=180°−∠AOB=90°−α.
∵AP平分∠BAO,BP平分∠ABO,
∴∠PAB+∠PBA=$\frac{1}{2}(\angle OAB+\angle OBA)=45°−\frac{1}{2}\alpha$,
∴∠APB=180°−$(45°−\frac{1}{2}\alpha )$=135°+$\frac{1}{2}\alpha$.(ii)①③④ [解析]①
∵BQ平分∠ABD,BM平分∠ABO,
∴∠MBQ=$\frac{1}{2}(\angle ABD+\angle ABO)=90°$,
∴∠Q+∠M=90°,故①为定值;②
∵AQ平分∠CAB,BQ平分∠ABD,
∴∠Q=180°−(∠QAB+∠QBA)=180°−[$\frac{1}{2}(180°−∠OAB)+\frac{1}{2}(180°−∠OBA)$]=$\frac{1}{2}(\angle OAB+\angle OBA)=\frac{1}{2}[180°−(90°+\alpha )]=45°−\frac{1}{2}\alpha$,
∴∠M=90°−∠Q=45°+$\frac{1}{2}\alpha$,
∴∠M−∠Q=α,故②不是定值;③
∵∠APB=135°+$\frac{1}{2}\alpha$,∠Q=45°−$\frac{1}{2}\alpha$,
∴∠APB+∠Q=135°+$\frac{1}{2}\alpha$+45°−$\frac{1}{2}\alpha$=180°,故③为定值;④
∵∠APB=135°+$\frac{1}{2}\alpha$,∠M=45°+$\frac{1}{2}\alpha$,
∴∠APB−∠M=135°+$\frac{1}{2}\alpha$−45°−$\frac{1}{2}\alpha$=90°,故④为定值.故答案为①③④.
(1)1 2 [解析]由题意,得$\left\{\begin{array}{l}y - x = 1,\\ 2y + 2x = 6,\end{array}\right.$解得$\left\{\begin{array}{l}x = 1,\\ y = 2.\end{array}\right.$
(2)不变化,∠APB=135°.如图
(1),
∵直线m⊥直线n,
∴∠AOB=90°,
∴∠OAB+∠OBA=90°.
∵AP平分∠BAO,BP平分∠ABO,
∴∠PAB+∠PBA=$\frac{1}{2}(\angle OAB+\angle ABO)=\frac{1}{2}× 90°=45°$,
∴∠APB=180°−45°=135°.
(3)(i)∠APB=135°+$\frac{1}{2}\alpha$.理由如下:根据题意,得∠AOB=90°+α,
∴∠OAB+∠OBA=180°−∠AOB=90°−α.
∵AP平分∠BAO,BP平分∠ABO,
∴∠PAB+∠PBA=$\frac{1}{2}(\angle OAB+\angle OBA)=45°−\frac{1}{2}\alpha$,
∴∠APB=180°−$(45°−\frac{1}{2}\alpha )$=135°+$\frac{1}{2}\alpha$.(ii)①③④ [解析]①
∵BQ平分∠ABD,BM平分∠ABO,
∴∠MBQ=$\frac{1}{2}(\angle ABD+\angle ABO)=90°$,
∴∠Q+∠M=90°,故①为定值;②
∵AQ平分∠CAB,BQ平分∠ABD,
∴∠Q=180°−(∠QAB+∠QBA)=180°−[$\frac{1}{2}(180°−∠OAB)+\frac{1}{2}(180°−∠OBA)$]=$\frac{1}{2}(\angle OAB+\angle OBA)=\frac{1}{2}[180°−(90°+\alpha )]=45°−\frac{1}{2}\alpha$,
∴∠M=90°−∠Q=45°+$\frac{1}{2}\alpha$,
∴∠M−∠Q=α,故②不是定值;③
∵∠APB=135°+$\frac{1}{2}\alpha$,∠Q=45°−$\frac{1}{2}\alpha$,
∴∠APB+∠Q=135°+$\frac{1}{2}\alpha$+45°−$\frac{1}{2}\alpha$=180°,故③为定值;④
∵∠APB=135°+$\frac{1}{2}\alpha$,∠M=45°+$\frac{1}{2}\alpha$,
∴∠APB−∠M=135°+$\frac{1}{2}\alpha$−45°−$\frac{1}{2}\alpha$=90°,故④为定值.故答案为①③④.