1.(2025·黑龙江期末)如图,在△ABC 中,$\angle C= 90^\circ$,BD 是△ABC 的角平分线. 若 CD= 3 cm,则点 D 到 AB 的距离为(
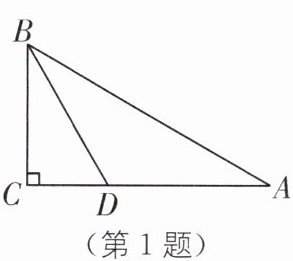
A.2 cm
B.3 cm
C.4 cm
D.5 cm
B
).
A.2 cm
B.3 cm
C.4 cm
D.5 cm
答案:B
解析:
过点$D$作$DE \perp AB$于点$E$。
因为$\angle C = 90^\circ$,所以$DC \perp BC$。
又因为$BD$是$\triangle ABC$的角平分线,且$DE \perp AB$,$DC \perp BC$,
根据角平分线的性质,角平分线上的点到角两边的距离相等,可得$DE = CD$。
已知$CD = 3\ cm$,所以$DE = 3\ cm$,即点$D$到$AB$的距离为$3\ cm$。
B
因为$\angle C = 90^\circ$,所以$DC \perp BC$。
又因为$BD$是$\triangle ABC$的角平分线,且$DE \perp AB$,$DC \perp BC$,
根据角平分线的性质,角平分线上的点到角两边的距离相等,可得$DE = CD$。
已知$CD = 3\ cm$,所以$DE = 3\ cm$,即点$D$到$AB$的距离为$3\ cm$。
B
2.(2025·宿迁泗阳期中)如图,BD 是△ABC 的角平分线,DE⊥AB,垂足为 E. 若△ABC 的面积为 70,AB= 16,BC= 12,则 DE 的长为(

A.4
B.5
C.10
D.28
B
).
A.4
B.5
C.10
D.28
答案:B [解析]如图,过点D作DF⊥BC于F,
∵BD是△ABC的角平分线,DE⊥AB,
∴DE=DF,${S}_{\triangle ABC}=\frac{1}{2}× 16DE+\frac{1}{2}× 12DF=70$,
∴14DE=70,解得DE=5.故选B
∵BD是△ABC的角平分线,DE⊥AB,
∴DE=DF,${S}_{\triangle ABC}=\frac{1}{2}× 16DE+\frac{1}{2}× 12DF=70$,
∴14DE=70,解得DE=5.故选B
3. 教材 P38 练习 T1·变式(2024·扬州仪征期中)在 9×7 的网格中,∠AOB 的位置如图所示,则到∠AOB 两边距离相等的点是
M
.答案:M [解析]∠AOB平分线上的点到∠AOB两边的距离相等.故满足条件的点是M.
4.(2024·安徽铜陵期中)如图,在△ABC 中,$\angle C= 90^\circ$,DE⊥AB. 若 CD= 3,AB= 10,△ABD 的面积为 15,则 AD 是∠BAC 的平分线吗?请说明理由.


答案:AD是∠BAC的平分线.理由如下:
∵AB=10,△ABD的面积为15,DE⊥AB,
∴DE=$\frac{15×2}{10}$=3,
∴DE=CD.
∵∠C=90°,DE⊥AB,
∴AD是∠BAC的平分线
∵AB=10,△ABD的面积为15,DE⊥AB,
∴DE=$\frac{15×2}{10}$=3,
∴DE=CD.
∵∠C=90°,DE⊥AB,
∴AD是∠BAC的平分线
5.(2025·山西晋中榆次区期中)如图,在△ABC 中,BO,CO 分别平分∠ABC,∠ACB,OD⊥BC 于点 D. 若 OD= 3,△ABC 的面积是 50,则△ABC 的周长为(

A.$\frac{50}{3}$
B.25
C.$\frac{100}{3}$
D.50
C
).
A.$\frac{50}{3}$
B.25
C.$\frac{100}{3}$
D.50
答案:C
解析:
连接OA,过点O作OE⊥AB于E,OF⊥AC于F。
∵BO平分∠ABC,OD⊥BC,OE⊥AB,
∴OE=OD=3。
同理,OF=OD=3。
∵S△ABC=S△OAB+S△OBC+S△OAC,
∴50=$\frac{1}{2}$×AB×OE+$\frac{1}{2}$×BC×OD+$\frac{1}{2}$×AC×OF。
即50=$\frac{1}{2}$×AB×3+$\frac{1}{2}$×BC×3+$\frac{1}{2}$×AC×3,
50=$\frac{3}{2}$(AB+BC+AC),
∴AB+BC+AC=$\frac{100}{3}$。
C
∵BO平分∠ABC,OD⊥BC,OE⊥AB,
∴OE=OD=3。
同理,OF=OD=3。
∵S△ABC=S△OAB+S△OBC+S△OAC,
∴50=$\frac{1}{2}$×AB×OE+$\frac{1}{2}$×BC×OD+$\frac{1}{2}$×AC×OF。
即50=$\frac{1}{2}$×AB×3+$\frac{1}{2}$×BC×3+$\frac{1}{2}$×AC×3,
50=$\frac{3}{2}$(AB+BC+AC),
∴AB+BC+AC=$\frac{100}{3}$。
C
6. 教材 P38 例 2·变式 如图,O 是△ABC 内一点,且 O 到△ABC 三边 AB,BC,CA 的距离 OE= OD= OF,若$\angle BAC= 70^\circ$,则$\angle BOC= $
125°
.答案:125°
解析:
∵OE=OD=OF,OE⊥AB,OD⊥BC,OF⊥AC,
∴点O是△ABC的内心,
∴BO平分∠ABC,CO平分∠ACB,
∵∠BAC=70°,
∴∠ABC+∠ACB=180°-70°=110°,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×110°=55°,
∴∠BOC=180°-55°=125°.
125°
7.(2024·盐城盐都实验学校期中)如图,OC 平分∠AOB,点 D,E 分别在 OA,OB 上,点 P 在 OC 上且有 PD= PE. 求证:$\angle PDO= \angle PEB$.


答案:如图,过点P作PF⊥OA于点F,PH⊥OB于点H.
∵OC平分∠AOB,
∴PF=PH.在Rt△PDF和Rt△PEH中,$\left\{\begin{array}{l}PD=PE,\\ PF=PH,\end{array}\right.$
∴Rt△PDF≌Rt△PEH(HL),
∴∠PDO=∠PEB.
∵OC平分∠AOB,
∴PF=PH.在Rt△PDF和Rt△PEH中,$\left\{\begin{array}{l}PD=PE,\\ PF=PH,\end{array}\right.$
∴Rt△PDF≌Rt△PEH(HL),
∴∠PDO=∠PEB.
8.(2025·扬州广陵区期中)如图,在△ABC 中,点 D 在 BC 边上,$\angle BAD= 110^\circ$,∠ABC 的平分线交 AC 于点 E,过点 E 作 EF⊥AB,垂足为 F,且$\angle AEF= 55^\circ$,连接 DE. 备用图

(1)求∠CAD 的度数;
(2)求证:DE 平分∠ADC;
(3)若 AB= 8,AD= 4,CD= 8,且$S_{\triangle ACD}= 15$,求△ABE 的面积.

(1)求∠CAD 的度数;
(2)求证:DE 平分∠ADC;
(3)若 AB= 8,AD= 4,CD= 8,且$S_{\triangle ACD}= 15$,求△ABE 的面积.
答案:
(1)
∵EF⊥AB,
∴∠F=90°.
∵∠AEF=55°,
∴∠BAE=∠F+∠AEF=90°+55°=145°.
∵∠BAE=∠BAD+∠CAD,∠BAD=110°,
∴∠CAD=∠BAE−∠BAD=145°−110°=35°.
(2)如图,过点E作EG⊥AD交AD于点G,EH⊥BC交BC于点H,
∵∠F=90°,∠AEF=55°,
∴∠EAF=90°−55°=35°.由
(1)可知,∠EAF=∠CAD=35°,
∴AE平分∠FAD.
∵EF⊥AF,EG⊥AD,
∴EF=EG.
∵BE平分∠ABC,EF⊥BF,EH⊥BC,
∴EF=EH,
∴EG=EH.
∵EG⊥AD,EH⊥BC,
∴DE平分∠ADC.
(3)
∵${S}_{\triangle ACD}=15$,
∴${S}_{\triangle ADE}+{S}_{\triangle CDE}=15$,
∴$\frac{1}{2}AD\cdot EG+\frac{1}{2}CD\cdot EH=15$.
∵AD=4,CD=8,EG=EH,
∴$\frac{1}{2}× 4EH+\frac{1}{2}× 8EH=15$,
∴EH=$\frac{15}{6}=\frac{5}{2}$,
∴EF=$\frac{5}{2}$.
∵AB=8,
∴${S}_{\triangle ABE}=\frac{1}{2}AB\cdot EF=\frac{1}{2}× 8× \frac{5}{2}=10$.
(1)
∵EF⊥AB,
∴∠F=90°.
∵∠AEF=55°,
∴∠BAE=∠F+∠AEF=90°+55°=145°.
∵∠BAE=∠BAD+∠CAD,∠BAD=110°,
∴∠CAD=∠BAE−∠BAD=145°−110°=35°.
(2)如图,过点E作EG⊥AD交AD于点G,EH⊥BC交BC于点H,
∵∠F=90°,∠AEF=55°,
∴∠EAF=90°−55°=35°.由
(1)可知,∠EAF=∠CAD=35°,
∴AE平分∠FAD.
∵EF⊥AF,EG⊥AD,
∴EF=EG.
∵BE平分∠ABC,EF⊥BF,EH⊥BC,
∴EF=EH,
∴EG=EH.
∵EG⊥AD,EH⊥BC,
∴DE平分∠ADC.
(3)
∵${S}_{\triangle ACD}=15$,
∴${S}_{\triangle ADE}+{S}_{\triangle CDE}=15$,
∴$\frac{1}{2}AD\cdot EG+\frac{1}{2}CD\cdot EH=15$.
∵AD=4,CD=8,EG=EH,
∴$\frac{1}{2}× 4EH+\frac{1}{2}× 8EH=15$,
∴EH=$\frac{15}{6}=\frac{5}{2}$,
∴EF=$\frac{5}{2}$.
∵AB=8,
∴${S}_{\triangle ABE}=\frac{1}{2}AB\cdot EF=\frac{1}{2}× 8× \frac{5}{2}=10$.