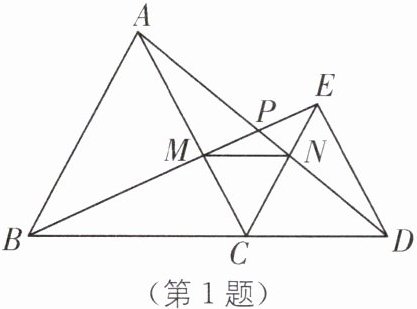
1. 手拉手模型(教材 P50 习题 T6·变式)如图,△ABC 和△DEC 都是等边三角形,D 是 BC 延长线上一点,AD 与 BE 相交于点 P,AC,BE 相交于点 M,AD,CE 相交于点 N,则下列五个结论:①AD= BE;②∠BMC= ∠ANC;③∠APM= 60°;④AN= BM;⑤△CMN 是等边三角形. 其中,正确的有(
A.2 个
B.3 个
C.4 个
D.5 个
]
D
).
A.2 个
B.3 个
C.4 个
D.5 个
]
答案:D [解析]
∵△ABC 和△DEC 都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,即∠BCE=∠ACD,∠ACE=60°,
∴△BCE≌△ACD(SAS),
∴AD=BE. 故结论①正确;
∵△BCE≌△ACD,
∴∠CBE=∠CAD.
∵∠ACB=∠ACE=60°,
∴∠BMC=∠ANC. 故结论②正确;
∵∠APM 是△PBD 的外角,
∴∠APM=∠CBE+∠ADC=∠CAD+∠ADC=∠ACB=60°. 故结论③正确;在△ACN 和△BCM 中,$\left\{\begin{array}{l} ∠CAN=∠CBM,\\ AC=BC,\\ ∠ACN=∠BCM=60^{\circ },\end{array}\right. $
∴△ACN≌△BCM(ASA),
∴AN=BM. 故结论④正确;
∵△ACN≌△BCM,
∴CM=CN.
∵∠MCN=60°,
∴△CMN 是等边三角形,故结论⑤正确. 故选 D.
∵△ABC 和△DEC 都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,即∠BCE=∠ACD,∠ACE=60°,
∴△BCE≌△ACD(SAS),
∴AD=BE. 故结论①正确;
∵△BCE≌△ACD,
∴∠CBE=∠CAD.
∵∠ACB=∠ACE=60°,
∴∠BMC=∠ANC. 故结论②正确;
∵∠APM 是△PBD 的外角,
∴∠APM=∠CBE+∠ADC=∠CAD+∠ADC=∠ACB=60°. 故结论③正确;在△ACN 和△BCM 中,$\left\{\begin{array}{l} ∠CAN=∠CBM,\\ AC=BC,\\ ∠ACN=∠BCM=60^{\circ },\end{array}\right. $
∴△ACN≌△BCM(ASA),
∴AN=BM. 故结论④正确;
∵△ACN≌△BCM,
∴CM=CN.
∵∠MCN=60°,
∴△CMN 是等边三角形,故结论⑤正确. 故选 D.
2.(2025·常州金坛期中)如图,BD 是等边三角形 ABC 的边 AC 上的高,以点 D 为圆心,DB 长为半径作弧交 BC 的延长线于点 E,则∠DEC= (

A.20°
B.25°
C.30°
D.35°
]
C
).
A.20°
B.25°
C.30°
D.35°
]
答案:C [解析]在等边三角形 ABC 中,∠ABC=60°,
∵BD 是 AC 边上的高,
∴BD 平分∠ABC,
∴∠CBD=$\frac{1}{2}$∠ABC=30°.
∵BD=ED,
∴∠DEC=∠CBD=30°. 故选 C.
∵BD 是 AC 边上的高,
∴BD 平分∠ABC,
∴∠CBD=$\frac{1}{2}$∠ABC=30°.
∵BD=ED,
∴∠DEC=∠CBD=30°. 故选 C.
3. 教材 P46 例 3·变式(2024·无锡锡山区期中)如图,在等边三角形 ABC 中,点 D,E 分别在边 BC,AC 上,且 DE//AB,过点 E 作 EF⊥DE,交 BC 的延长线于点 F.

(1)求∠F 的度数;
(2)若 CD= 2,求 DF 的长.

(1)求∠F 的度数;
(2)若 CD= 2,求 DF 的长.
答案:
(1)
∵△ABC 是等边三角形,
∴∠A=∠B=∠ACB=60°.
∵DE//AB,
∴∠B=∠EDC=60°,∠A=∠CED=60°,
∴∠EDC=∠ECD=∠DEC=60°.
∵EF⊥ED,
∴∠DEF=90°,
∴∠F=90°−60°=30°.
(2)
∵∠F+∠FEC=∠ECD=60°,
∴∠F=∠FEC=30°,
∴CE=CF.
∵∠EDC=∠ECD=∠DEC=60°,
∴CE=DC=2,
∴CF=2,
∴DF=DC+CF=2+2=4.
(1)
∵△ABC 是等边三角形,
∴∠A=∠B=∠ACB=60°.
∵DE//AB,
∴∠B=∠EDC=60°,∠A=∠CED=60°,
∴∠EDC=∠ECD=∠DEC=60°.
∵EF⊥ED,
∴∠DEF=90°,
∴∠F=90°−60°=30°.
(2)
∵∠F+∠FEC=∠ECD=60°,
∴∠F=∠FEC=30°,
∴CE=CF.
∵∠EDC=∠ECD=∠DEC=60°,
∴CE=DC=2,
∴CF=2,
∴DF=DC+CF=2+2=4.
4. 等边三角形两条中线相交所成的锐角的度数为( ).
A.30°
B.45°
C.60°
D.75°
A.30°
B.45°
C.60°
D.75°
答案:
C [解析]如图,△ABC 为等边三角形,BD,CE 分别为边 AC,AB 上的中线,交于点 O,
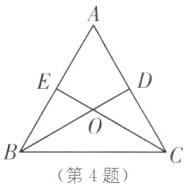
∴CE⊥AB,BD 平分∠ABC,
∴∠OEB=90°,∠EBO=$\frac{1}{2}$∠ABC =30°,
∴∠BOE=90°−30°=60°. 故选 C.
C [解析]如图,△ABC 为等边三角形,BD,CE 分别为边 AC,AB 上的中线,交于点 O,

∴CE⊥AB,BD 平分∠ABC,
∴∠OEB=90°,∠EBO=$\frac{1}{2}$∠ABC =30°,
∴∠BOE=90°−30°=60°. 故选 C.
5.(2024·宿迁宿城区期末)如图,∠AOB= 120°,OP 平分∠AOB,且 OP= 1. 若点 M,N 分别在 OA,OB 上,且△PMN 为等边三角形,则满足上述条件的△PMN 有( ).

A.1 个
B.2 个
C.3 个
D.无数个
]

A.1 个
B.2 个
C.3 个
D.无数个
]
答案:
D [解析]如图,过点 P 作 PM⊥OA 于 M,PN⊥OB 于 N.

∵OP 平分∠AOB,PM⊥OA 于 M,PN⊥OB 于 N,
∴PM=PN,∠PMO=90°,∠PNO=90°.
∴∠MPN=360°−∠AOB−∠PMO−∠PNO=60°,此时,△PMN 是等边三角形. 当 M 向 MO 方向移动,N 向 NB 方向移动,∠MPM₁=∠NPN₁时,
∴∠M₁PN₁=∠M₁PN+∠NPN₁=∠M₁PN+∠MPM₁=∠MPN=60°. 在△PMM₁和△PNN₁中,$\left\{\begin{array}{l} ∠PMM_{1}=∠PNN_{1},\\ PM=PN,\\ ∠MPM_{1}=∠NPN_{1},\end{array}\right. $
∴△PMM₁≌△PNN₁(ASA),
∴PM₁=PN₁,
∴△M₁PN₁是等边三角形.
∴当 M 向 MO 方向移动,N 向 NB 方向移动,∠MPM₁=∠NPN₁时,△M₁PN₁是等边三角形. 同理:当 M 向 MA 方向移动,N 向 NO 方向移动,也存在无数个满足条件的等边三角形 PMN. 综上所述,满足条件的△PMN 有无数个. 故选 D.
D [解析]如图,过点 P 作 PM⊥OA 于 M,PN⊥OB 于 N.

∵OP 平分∠AOB,PM⊥OA 于 M,PN⊥OB 于 N,
∴PM=PN,∠PMO=90°,∠PNO=90°.
∴∠MPN=360°−∠AOB−∠PMO−∠PNO=60°,此时,△PMN 是等边三角形. 当 M 向 MO 方向移动,N 向 NB 方向移动,∠MPM₁=∠NPN₁时,
∴∠M₁PN₁=∠M₁PN+∠NPN₁=∠M₁PN+∠MPM₁=∠MPN=60°. 在△PMM₁和△PNN₁中,$\left\{\begin{array}{l} ∠PMM_{1}=∠PNN_{1},\\ PM=PN,\\ ∠MPM_{1}=∠NPN_{1},\end{array}\right. $
∴△PMM₁≌△PNN₁(ASA),
∴PM₁=PN₁,
∴△M₁PN₁是等边三角形.
∴当 M 向 MO 方向移动,N 向 NB 方向移动,∠MPM₁=∠NPN₁时,△M₁PN₁是等边三角形. 同理:当 M 向 MA 方向移动,N 向 NO 方向移动,也存在无数个满足条件的等边三角形 PMN. 综上所述,满足条件的△PMN 有无数个. 故选 D.
6. 如图,等边三角形纸片 ABC 的边长为 6,E,F 是边 BC 上的三等分点. 分别过点 E,F 沿着平行于 BA,CA 方向各剪一刀,则剪下的△DEF 的周长是______
6
.答案:6
解析:
∵△ABC是等边三角形,边长为6,
∴BC=6,∠B=∠C=60°。
∵E,F是边BC上的三等分点,
∴BE=EF=FC=2。
∵DE//BA,DF//CA,
∴∠DEF=∠B=60°,∠DFE=∠C=60°,
∴△DEF是等边三角形,
∴DE=EF=FD=2,
∴△DEF的周长是2+2+2=6。
6
7. 以正方形 ABCD 的一边 CD 为边作等边三角形 CDE. 连接 AE,BE.
(1)画出图形;
(2)求∠AEB 的度数.
(1)画出图形;
(2)求∠AEB 的度数.
答案:
(1)当点 E 在正方形 ABCD 外时,如图(1);当点 E 在正方形 ABCD 内时,如图(2).

(2)在图(1)中,
∵∠ADE=∠ADC+∠CDE=90°+60°=150°,AD=CD=DE,
∴∠DEA=∠DAE=15°. 同理∠CEB=15°.
∴∠AEB=∠DEC−∠DEA−∠CEB=60°−15°−15°=30°. 在图
(2)中,
∵AD=CD=DE,∠ADE=∠ADC−∠CDE=90°−60°=30°,
∴∠AED=∠DAE=75°. 同理∠CEB=75°.
∴∠AEB=360°−∠AED−∠CEB−∠CED=360°−75°−75°−60°=150°. 综上所述,∠AEB 的度数为 30°或 150°.
(1)当点 E 在正方形 ABCD 外时,如图(1);当点 E 在正方形 ABCD 内时,如图(2).

(2)在图(1)中,
∵∠ADE=∠ADC+∠CDE=90°+60°=150°,AD=CD=DE,
∴∠DEA=∠DAE=15°. 同理∠CEB=15°.
∴∠AEB=∠DEC−∠DEA−∠CEB=60°−15°−15°=30°. 在图
(2)中,
∵AD=CD=DE,∠ADE=∠ADC−∠CDE=90°−60°=30°,
∴∠AED=∠DAE=75°. 同理∠CEB=75°.
∴∠AEB=360°−∠AED−∠CEB−∠CED=360°−75°−75°−60°=150°. 综上所述,∠AEB 的度数为 30°或 150°.
8.(2025·扬州广陵区期中)已知:如图,在四边形 ABCD 中,∠ABC= ∠ADC= 90°,点 E 是 AC 的中点.
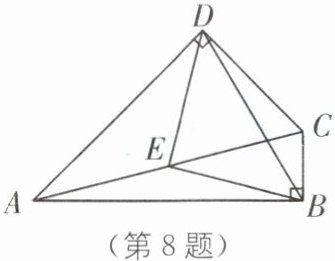
(1)求证:△BED 是等腰三角形;
(2)当∠BCD= ______°时,△BED 是等边三角形.
(1)∵∠ABC=∠ADC=90°,点 E 是 AC 边的中点,
∴BE=$\frac{1}{2}$AC,DE=$\frac{1}{2}$AC,
∴BE=DE,
∴△BED 是等腰三角形.
(2)当∠BCD=

(1)求证:△BED 是等腰三角形;
(2)当∠BCD= ______°时,△BED 是等边三角形.
(1)∵∠ABC=∠ADC=90°,点 E 是 AC 边的中点,
∴BE=$\frac{1}{2}$AC,DE=$\frac{1}{2}$AC,
∴BE=DE,
∴△BED 是等腰三角形.
(2)当∠BCD=
150
°时,△BED 是等边三角形.答案:
(1)
∵∠ABC=∠ADC=90°,点 E 是 AC 边的中点,
∴BE=$\frac{1}{2}$AC,DE=$\frac{1}{2}$AC,
∴BE=DE,
∴△BED 是等腰三角形.
(2)150 [解析]
∵AE=ED,
∴∠DAE=∠EDA.
∵AE=BE,
∴∠EAB=∠EBA.
∵∠DAE+∠EDA=∠DEC,∠EAB+∠EBA=∠BEC,
∴∠DAB=$\frac{1}{2}$∠DEB.
∵△BED 是等边三角形,
∴∠DEB=60°,
∴∠BAD=30°,
∴∠BCD=360°−90°−90°−30°=150°.
(1)
∵∠ABC=∠ADC=90°,点 E 是 AC 边的中点,
∴BE=$\frac{1}{2}$AC,DE=$\frac{1}{2}$AC,
∴BE=DE,
∴△BED 是等腰三角形.
(2)150 [解析]
∵AE=ED,
∴∠DAE=∠EDA.
∵AE=BE,
∴∠EAB=∠EBA.
∵∠DAE+∠EDA=∠DEC,∠EAB+∠EBA=∠BEC,
∴∠DAB=$\frac{1}{2}$∠DEB.
∵△BED 是等边三角形,
∴∠DEB=60°,
∴∠BAD=30°,
∴∠BCD=360°−90°−90°−30°=150°.