9. 如图,△ABC 是等边三角形,O 为△ABC 内任意一点,OE//AB,OF//AC,分别交 BC 于点 E,F. 求证:△OEF 是等边三角形.
]

]

答案:
∵△ABC 是等边三角形,
∴∠B=∠C=60°.
∵OE//AB,
∴∠OEF=∠B=60°.
∵OF/AC,
∴∠OFE=∠C=60°,
∴∠EOF=∠OEF=∠OFE=60°,
∴△OEF 是等边三角形.
∵△ABC 是等边三角形,
∴∠B=∠C=60°.
∵OE//AB,
∴∠OEF=∠B=60°.
∵OF/AC,
∴∠OFE=∠C=60°,
∴∠EOF=∠OEF=∠OFE=60°,
∴△OEF 是等边三角形.
10.(2025·扬州广陵区期中)如图(1),在四边形 ABCD 中,DC//AB,AD= BC,BD 平分∠ABC.
(1)求证:AD= DC;
(2)如图(2),在上述条件下,若∠A= ∠ABC= 60°,过点 D 作 DE⊥AB,过点 C 作 CF⊥BD,垂足分别为 E,F,连接 EF. 判断△DEF 的形状并证明你的结论.
]

(1)求证:AD= DC;
(2)如图(2),在上述条件下,若∠A= ∠ABC= 60°,过点 D 作 DE⊥AB,过点 C 作 CF⊥BD,垂足分别为 E,F,连接 EF. 判断△DEF 的形状并证明你的结论.
]

答案:
(1)
∵DC//AB,
∴∠CDB=∠ABD. 又 BD 平分∠ABC,
∴∠CBD=∠ABD.
∴∠CDB=∠CBD,
∴BC=DC. 又 AD=BC,
∴AD=DC.
(2)△DEF 为等边三角形,证明如下:
∵BC=DC(已证),CF⊥BD,
∴点 F 是 BD 的中点.
∵∠DEB=90°,
∴EF=DF=BF.
∵∠ABC=60°,BD 平分∠ABC,
∴∠DBE=30°,∠BDE=60°,
∴△DEF 为等边三角形.
(1)
∵DC//AB,
∴∠CDB=∠ABD. 又 BD 平分∠ABC,
∴∠CBD=∠ABD.
∴∠CDB=∠CBD,
∴BC=DC. 又 AD=BC,
∴AD=DC.
(2)△DEF 为等边三角形,证明如下:
∵BC=DC(已证),CF⊥BD,
∴点 F 是 BD 的中点.
∵∠DEB=90°,
∴EF=DF=BF.
∵∠ABC=60°,BD 平分∠ABC,
∴∠DBE=30°,∠BDE=60°,
∴△DEF 为等边三角形.
11.(2024·徐州邳州期中)如图,在等边三角形 ABC 中,点 P 在△ABC 内,点 Q 在△ABC 外,且∠ABP= ∠ACQ,BP= CQ,问△APQ 是什么形状的三角形?试说明你的结论.
]

]

答案:△APQ 为等边三角形. 证明如下:
∵△ABC 为等边三角形,
∴AB=AC. 在△ABP 与△ACQ 中,$\left\{\begin{array}{l} AB=AC,\\ ∠ABP=∠ACQ,\\ BP=CQ,\end{array}\right. $
∴△ABP≌△ACQ(SAS),
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ 是等边三角形.
∵△ABC 为等边三角形,
∴AB=AC. 在△ABP 与△ACQ 中,$\left\{\begin{array}{l} AB=AC,\\ ∠ABP=∠ACQ,\\ BP=CQ,\end{array}\right. $
∴△ABP≌△ACQ(SAS),
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ 是等边三角形.
12.(2024·南京师大附中月考)已知:如图,在△ABC 中,AB= AC,∠BAC= 120°,AB,AC 边的垂直平分线分别交 BC 于点 E,D,连接 AE,AD. 求证:△AED 是等边三角形.
]

]

答案:
∵AB=AC,∠BAC=120°,
∴∠B=∠C=$\frac{1}{2}$×(180°−120°)=30°.
∵AB,AC 边的垂直平分线分别交 BC 于点 E,D,
∴AE=BE,AD=CD,
∴∠BAE=∠B=30°,∠CAD=∠C=30°,
∴∠AED=∠B+∠BAE=60°,∠ADE=∠C+∠CAD=60°,
∴∠DAE=180°−∠AED−∠ADE=60°,
∴△ADE 是等边三角形.
∵AB=AC,∠BAC=120°,
∴∠B=∠C=$\frac{1}{2}$×(180°−120°)=30°.
∵AB,AC 边的垂直平分线分别交 BC 于点 E,D,
∴AE=BE,AD=CD,
∴∠BAE=∠B=30°,∠CAD=∠C=30°,
∴∠AED=∠B+∠BAE=60°,∠ADE=∠C+∠CAD=60°,
∴∠DAE=180°−∠AED−∠ADE=60°,
∴△ADE 是等边三角形.
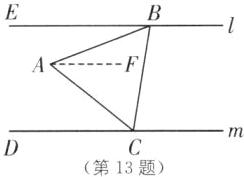
13.(2024·泰安中考)如图,直线 l//m,等边三角形 ABC 的两个顶点 B,C 分别落在直线 l,m 上,若∠ABE= 21°,则∠ACD 的度数是( ).

A.45°
B.39°
C.29°
D.21°
]

A.45°
B.39°
C.29°
D.21°
]
答案:
B [解析]如图,过点 A 作 AF//l,
∵直线 l//m,
∴AF//m.
∵△ABC 是等边三角形,
∴∠BAC=60°.
∵AF//l,
∴∠BAF=∠ABE.
∵∠ABE=21°,
∴∠BAF=21°,
∴∠CAF=∠BAC−∠BAF=60°−21°=39°.
∵AF//m,
∴∠ACD=∠CAF=39°. 故选 B.
B [解析]如图,过点 A 作 AF//l,

∵直线 l//m,
∴AF//m.
∵△ABC 是等边三角形,
∴∠BAC=60°.
∵AF//l,
∴∠BAF=∠ABE.
∵∠ABE=21°,
∴∠BAF=21°,
∴∠CAF=∠BAC−∠BAF=60°−21°=39°.
∵AF//m,
∴∠ACD=∠CAF=39°. 故选 B.