1.(2025·宿迁沭阳期中)下列各说法中,正确的个数有(
①若|x|= x,则x一定是正数;
②倒数为本身的数是1;
③0是最小的有理数;
④若|a|= |b|,则a= ±b.
A.0个
B.1个
C.2个
D.3个
B
).①若|x|= x,则x一定是正数;
②倒数为本身的数是1;
③0是最小的有理数;
④若|a|= |b|,则a= ±b.
A.0个
B.1个
C.2个
D.3个
答案:1.B 解析 ①若|x|=x,则x一定是正数,错误,x也可能等于0,①不符合题意;②倒数为本身的数是1或-1,②不符合题意;③0是最小的有理数,错误,0是绝对值最小的有理数,③不符合题意;④若|a|=|b|,则a=±b,正确,④符合题意.故正确的说法只有1个.故选B.
2.(2024·临夏州中考)下列各数中,是无理数的是(
A.$\frac{\pi}{2}$
B.$\frac{1}{3}$
C.$\sqrt[3]{27}$
D.0.13133
A
).A.$\frac{\pi}{2}$
B.$\frac{1}{3}$
C.$\sqrt[3]{27}$
D.0.13133
答案:2.A 解析 A.$\frac{π}{2}$是无理数.故此选项符合题意;B.$\frac{1}{3}$是有理数.故此选项不符合题意;C.$\sqrt[3]{27}=3$,是有理数.故此选项不符合题意;D.0.131 33是有理数.故此选项不符合题意.故选A.
3.(2024·淄博中考)下列运算结果是正数的是(
A.$3^{-1}$
B.$-3^2$
C.$-|-3|$
D.$-\sqrt{3}$
A
).A.$3^{-1}$
B.$-3^2$
C.$-|-3|$
D.$-\sqrt{3}$
答案:3.A 解析 A.$3^{-1}=\frac{1}{3}>0$.故此选项符合题意;B.$-3^2=-9<0$.故此选项不符合题意;C.$-|-3|=-3<0$.故此选项不符合题意;D.$-\sqrt{3}<0$.故此选项不符合题意.故选A.
4. 实验班原创 $1-\sqrt{7}$的相反数是
$\sqrt{7}-1$
;$\sqrt[3]{-64}$的绝对值是4
.答案:4.$\sqrt{7}-1$ 4
5.(2025·南通海安月考)(1)已知$2a+3$的立方根是3,$10+3b$的平方根是±4,c是$\sqrt{19}$的整数部分,求$a-5b+c$的平方根;
(2)已知$\sqrt[3]{1-2x}与\sqrt[3]{3x-7}$互为相反数,求$\sqrt{10x+4}$的值.
(2)已知$\sqrt[3]{1-2x}与\sqrt[3]{3x-7}$互为相反数,求$\sqrt{10x+4}$的值.
答案:5.
(1)
∵2a+3的立方根是3,10+3b的平方根是±4,
∴2a+3=27,10+3b=16,解得a=12,b=2.
∵4<$\sqrt{19}$<5,
∴$\sqrt{19}$的整数部分c=4,
∴a-5b+c=12-5×2+4=12-10+4=6,
∴a-5b+c的平方根为±$\sqrt{6}$.
(2)
∵$\sqrt[3]{1-2x}$与$\sqrt[3]{3x-7}$互为相反数,
∴1-2x+3x-7=0,解得x=6,
∴$\sqrt{10x+4}=\sqrt{10×6+4}=\sqrt{64}=8$.
(1)
∵2a+3的立方根是3,10+3b的平方根是±4,
∴2a+3=27,10+3b=16,解得a=12,b=2.
∵4<$\sqrt{19}$<5,
∴$\sqrt{19}$的整数部分c=4,
∴a-5b+c=12-5×2+4=12-10+4=6,
∴a-5b+c的平方根为±$\sqrt{6}$.
(2)
∵$\sqrt[3]{1-2x}$与$\sqrt[3]{3x-7}$互为相反数,
∴1-2x+3x-7=0,解得x=6,
∴$\sqrt{10x+4}=\sqrt{10×6+4}=\sqrt{64}=8$.
6. 数形结合思想 (2025·南京联合体月考)如图,直径为单位1的圆从数轴上表示1的点沿着数轴无滑动地逆时针滚动一周到达点A,则此时点A表示的数是(
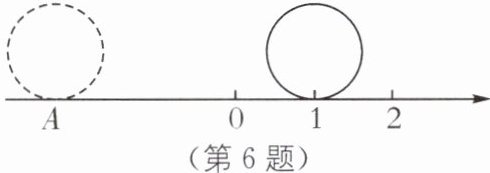
A.$\pi+1$
B.$-\pi-1$
C.$-\pi+1$
D.$\pi-1$
C
).
A.$\pi+1$
B.$-\pi-1$
C.$-\pi+1$
D.$\pi-1$
答案:6.C 解析
∵圆的周长为1×π=π,
∴点A表示的数为1-π.故选C.
∵圆的周长为1×π=π,
∴点A表示的数为1-π.故选C.
7. 传统文化 秦九韶公式 (2024·盐城亭湖区期中)我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的公式,即三角形的三边长分别为a,b,c,记$p= \frac{a+b+c}{2}$,那么其面积$S= \sqrt{p(p-a)(p-b)(p-c)}$.若某个三角形的三边长分别为2,3,3,其面积S介于哪两个整数之间(
A.1与2
B.2与3
C.3与4
D.4与5
B
).A.1与2
B.2与3
C.3与4
D.4与5
答案:7.B 解析 根据题意,得三角形的三边长分别为2,3,3,则p=$\frac{2+3+3}{2}=4$,
∴其面积S=$\sqrt{4×(4-2)×(4-3)×(4-3)}=\sqrt{8}$.
∵4<8<9,
∴$\sqrt{4}<\sqrt{8}<\sqrt{9}$,
∴2<$\sqrt{8}$<3.故选B.
∴其面积S=$\sqrt{4×(4-2)×(4-3)×(4-3)}=\sqrt{8}$.
∵4<8<9,
∴$\sqrt{4}<\sqrt{8}<\sqrt{9}$,
∴2<$\sqrt{8}$<3.故选B.
8.(2024·德州中考)实数a,b在数轴上对应点的位置如图所示,下列结论正确的是(

A.$|a|>|b|$
B.$a+b<0$
C.$a+2>b+2$
D.$|a-1|>|b-1|$
D
).
A.$|a|>|b|$
B.$a+b<0$
C.$a+2>b+2$
D.$|a-1|>|b-1|$
答案:8.D 解析 根据实数a,b在数轴上对应点的位置,得-1<a<0,1<b<2,
∴|a|<|b|,a+b>0,a<b,|a-1|>|b-1|.故选项A,B不正确,不符合题意;选项D正确,符合题意;
∵a<b,
∴a+2<b+2.故选项C不正确,不符合题意.故选D.
∴|a|<|b|,a+b>0,a<b,|a-1|>|b-1|.故选项A,B不正确,不符合题意;选项D正确,符合题意;
∵a<b,
∴a+2<b+2.故选项C不正确,不符合题意.故选D.
9.(山东泰安泰山实验中学自主招生)如图,数轴上A,B两点表示的数分别为1和$\sqrt{3}$,点B关于点A的对称点为点C,则点C所表示的数是(

A.$-1$
B.$1-\sqrt{3}$
C.$2-\sqrt{3}$
D.$-2$
C
).
A.$-1$
B.$1-\sqrt{3}$
C.$2-\sqrt{3}$
D.$-2$
答案:9.C 解析 设点C所表示的数为x.
∵数轴上A,B两点表示的数分别为1和$\sqrt{3}$,
∴AB=$\sqrt{3}-1$.根据题意,得1-x=$\sqrt{3}-1$,解得x=2-$\sqrt{3}$.故选C.
∵数轴上A,B两点表示的数分别为1和$\sqrt{3}$,
∴AB=$\sqrt{3}-1$.根据题意,得1-x=$\sqrt{3}-1$,解得x=2-$\sqrt{3}$.故选C.