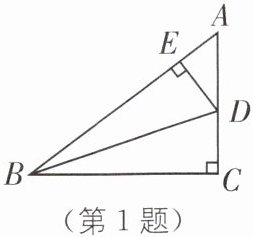
1.(2025·南京联合体期中)如图,在△ABC中,∠C= 90°,BD是△ABC的角平分线,DE⊥AB,垂足为E. 若AC= 3,BC= 4,则△AED的周长为(
A.3
B.4
C.5
D.6
B
).
A.3
B.4
C.5
D.6
答案:B [解析]
∵∠C=90°,
∴DC⊥BC.又BD是∠ABC的平分线,DE⊥AB,
∴DC=DE,∠EBD=∠CBD.在Rt△EBD和Rt△CBD中,{DE=DC,BD=BD}
∴Rt△EBD≌Rt△CBD(HL),
∴BC=BE=4.
∵AB=√(AC²+BC²)=√(3²+4²)=5,
∴AE=5 - 4=1,
∴△AED的周长=AD+DE+AE=AC+AE=3+1=4.故选B.归纳总结 本题考查角平分线的性质定理及勾股定理,解题关键是利用勾股定理求线段的长.
∵∠C=90°,
∴DC⊥BC.又BD是∠ABC的平分线,DE⊥AB,
∴DC=DE,∠EBD=∠CBD.在Rt△EBD和Rt△CBD中,{DE=DC,BD=BD}
∴Rt△EBD≌Rt△CBD(HL),
∴BC=BE=4.
∵AB=√(AC²+BC²)=√(3²+4²)=5,
∴AE=5 - 4=1,
∴△AED的周长=AD+DE+AE=AC+AE=3+1=4.故选B.归纳总结 本题考查角平分线的性质定理及勾股定理,解题关键是利用勾股定理求线段的长.
2. 如图,在△ABC中,∠C= 90°,AB的中垂线DE交AB于点E,交AC于点D,若AB= 15,BC= 9,则△BCD的周长为(

A.16
B.20
C.21
D.24
C
).
A.16
B.20
C.21
D.24
答案:C [解析]
∵∠C=90°,AB=15,BC=9,
∴AC²=AB² - BC²=15² - 9²=144,
∴AC=12.
∵DE是线段AB的垂直平分线,
∴AD=BD,
∴AD+CD=BD+CD,即BD+CD=AC,
∴△BCD的周长为CD+BD+BC=AC+BC=12+9=21.故选C.归纳总结 本题考查的是勾股定理及线段垂直平分线的性质,能根据线段垂直平分线的性质,求出BD + CD=AC 是解答此题的关键
∵∠C=90°,AB=15,BC=9,
∴AC²=AB² - BC²=15² - 9²=144,
∴AC=12.
∵DE是线段AB的垂直平分线,
∴AD=BD,
∴AD+CD=BD+CD,即BD+CD=AC,
∴△BCD的周长为CD+BD+BC=AC+BC=12+9=21.故选C.归纳总结 本题考查的是勾股定理及线段垂直平分线的性质,能根据线段垂直平分线的性质,求出BD + CD=AC 是解答此题的关键
3.(2024·镇江句容期末)如图,在△ABC中,∠ACB= 90°,分别以AC,AB为边长向外作正方形,且它们的面积分别为9和25,则BC的长为

4
.
答案:4
解析:
在$Rt\triangle ABC$中,$\angle ACB=90^\circ$。
因为以$AC$为边长的正方形面积为$9$,所以$AC^2 = 9$。
以$AB$为边长的正方形面积为$25$,所以$AB^2 = 25$。
由勾股定理得$BC^2=AB^2 - AC^2=25 - 9=16$,则$BC=\sqrt{16}=4$。
4
因为以$AC$为边长的正方形面积为$9$,所以$AC^2 = 9$。
以$AB$为边长的正方形面积为$25$,所以$AB^2 = 25$。
由勾股定理得$BC^2=AB^2 - AC^2=25 - 9=16$,则$BC=\sqrt{16}=4$。
4
4. 方程思想(2025·淮安淮安区期中)如图,在Rt△ABC中,∠C= 90°,AC= 8,BC= 6,AD为△ABC的角平分线. 求CD的长度.


答案:如图,过点D作DP⊥AB于点P,在Rt△ABC中,AC=8,BC=6,
∴AB=√(AC²+BC²)=√(8²+6²)=10.
∵∠CAD=∠PAD,∠C=∠APD=90°,AD=AD,
∴△ADC≌△ADP(AAS),
∴AC=AP=8,CD=PD.设CD=PD=x,在Rt△BDP中,PB=AB - AP=2,BD=6 - x,
∴x²+2²=(6 - x)²,
∴x=8/3.
∴CD=8/3.
∴AB=√(AC²+BC²)=√(8²+6²)=10.
∵∠CAD=∠PAD,∠C=∠APD=90°,AD=AD,
∴△ADC≌△ADP(AAS),
∴AC=AP=8,CD=PD.设CD=PD=x,在Rt△BDP中,PB=AB - AP=2,BD=6 - x,
∴x²+2²=(6 - x)²,
∴x=8/3.
∴CD=8/3.
5. 教材P89练习T2·变式(2024·陕西咸阳兴平期末)如图,在Rt△ABC中,分别以这个三角形的三边为边长向外侧作正方形,面积分别记为$S_1,S_2,S_3. $若$S_3+S_2-S_1= 18,$则图中阴影部分的面积为(
A.6
B.$\frac{9}{2}$
C.5
D.$\frac{7}{2}$
B
).A.6
B.$\frac{9}{2}$
C.5
D.$\frac{7}{2}$
答案:B [解析]在Rt△ABC中,由勾股定理,得AC²+AB²=BC²,即S₁+S₂=S₃.
∵S₃+S₂ - S₁=18,
∴S₂=9.由题图可知,阴影部分的面积=1/2S₂,
∴阴影部分的面积=9/2,故选B.
∵S₃+S₂ - S₁=18,
∴S₂=9.由题图可知,阴影部分的面积=1/2S₂,
∴阴影部分的面积=9/2,故选B.
6. 教材P91习题T4·拓展 我们在学习勾股定理的第二课时时,下列图形可以用来验证勾股定理的有(

A.1个
B.2个
C.3个
D.4个
C
). 
A.1个
B.2个
C.3个
D.4个
答案:C [解析]由题图
(1)和题图
(3),可得S_{梯形}=1/2(a + b)·(a + b),S_{梯形}=1/2ab+1/2ab+1/2c²,
∴1/2×(a + b)(a + b)=1/2ab+1/2ab+1/2c²,
∴a²+2ab+b²=ab+ab+c²,
∴a²+b²=c²,故题图
(1)和题图
(3)都可以验证勾股定理;题图
(2)中,图形的总面积可以表示为c²+2×1/2ab=c²+ab,也可以表示为a²+b²+2×1/2ab=a²+b²+ab,
∴c²+ab=a²+b²+ab,
∴a²+b²=c²,故题图
(2)可以验证勾股定理;题图
(4)不可以验证勾股定理.综上所述,题图
(1)、题图
(2)和题图
(3)可以验证勾股定理,共3个.故选C.
(1)和题图
(3),可得S_{梯形}=1/2(a + b)·(a + b),S_{梯形}=1/2ab+1/2ab+1/2c²,
∴1/2×(a + b)(a + b)=1/2ab+1/2ab+1/2c²,
∴a²+2ab+b²=ab+ab+c²,
∴a²+b²=c²,故题图
(1)和题图
(3)都可以验证勾股定理;题图
(2)中,图形的总面积可以表示为c²+2×1/2ab=c²+ab,也可以表示为a²+b²+2×1/2ab=a²+b²+ab,
∴c²+ab=a²+b²+ab,
∴a²+b²=c²,故题图
(2)可以验证勾股定理;题图
(4)不可以验证勾股定理.综上所述,题图
(1)、题图
(2)和题图
(3)可以验证勾股定理,共3个.故选C.
7.(南京中华中学特长生)在直角三角形中,直角边长分别为a,b,斜边长为c,则$a^3+b^3$
<
$c^3($填“>”“<”或“=”).答案:< [解析]
∵0 < a < c,0 < b < c,
∴a³ < a²c,b³ < b²c,
∴a³+b³ < a²c+b²c.
∵a²+b²=c²,
∴a²c+b²c=c²·c=c³,
∴a³+b³ < c³.
∵0 < a < c,0 < b < c,
∴a³ < a²c,b³ < b²c,
∴a³+b³ < a²c+b²c.
∵a²+b²=c²,
∴a²c+b²c=c²·c=c³,
∴a³+b³ < c³.
8. 等积法(2025·泰州兴化期中)如图,在△ABC中,∠BAC= 90°,AB= 15,AC= 20.
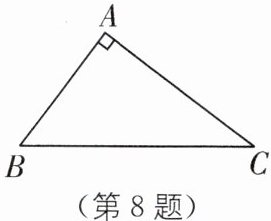
(1)求BC的值;
(2)过点A作AD⊥BC,垂足为D,求BD的值.

(1)求BC的值;
(2)过点A作AD⊥BC,垂足为D,求BD的值.
答案:
(1)在△ABC中,∠BAC=90°,AB=15,AC=20,
∴BC=√(AB²+AC²)=√(15²+20²)=25.
(2)如图,过点A作AD⊥BC于点D,
∴S_{△ABC}=1/2AB·AC=1/2BC·AD,
∴AD=(AB·AC)/BC=(15×20)/25=12,
∴BD=√(AB² - AD²)=√(15² - 12²)=9.
(1)在△ABC中,∠BAC=90°,AB=15,AC=20,
∴BC=√(AB²+AC²)=√(15²+20²)=25.
(2)如图,过点A作AD⊥BC于点D,
∴S_{△ABC}=1/2AB·AC=1/2BC·AD,
∴AD=(AB·AC)/BC=(15×20)/25=12,
∴BD=√(AB² - AD²)=√(15² - 12²)=9.