1. (教材P90尝试T1·变式)如图,在四边形ABCD中,∠ABC= ∠ADC= 90°,分别以四边为边长向外作正方形甲、乙、丙、丁,如果用S甲,S乙,S丙,S丁来表示它们的面积,那么下列结论正确的是(
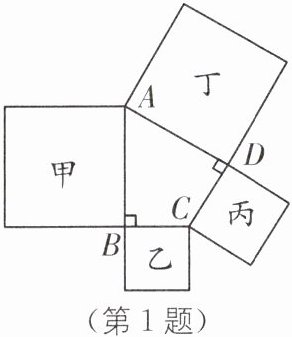
A.S甲= S丁
B.S乙= S丙
C.S甲+S乙= S丙+S丁
D.S甲-S乙= S丙-S丁
C
).
A.S甲= S丁
B.S乙= S丙
C.S甲+S乙= S丙+S丁
D.S甲-S乙= S丙-S丁
答案:C [解析]连接AC.由勾股定理,得AB²+BC²=AC²,AD²+CD²=AC²,
∴S甲+S乙=S丙+S丁.故选C 归纳总结 本题考查了勾股定理的知识,关键是能够运用勾股定理证明4个正方形的面积之间的关系。
∴S甲+S乙=S丙+S丁.故选C 归纳总结 本题考查了勾股定理的知识,关键是能够运用勾股定理证明4个正方形的面积之间的关系。
2. (2024·淮安涟水期中)如图,在△ABC中,∠C= 90°,点D是BC上的一点,且BD= 2,DC= 3,则$AB^{2}-AD^{2}$的值为(
A.4
B.9
C.16
D.25
C
).A.4
B.9
C.16
D.25
答案:C [解析]在Rt△ABC与Rt△ACD中,由勾股定理,得AB²=AC²+BC²,AD²=AC²+CD²,
∴AB²−AD²=BC²−CD²=(BD+CD)²−CD²=5²−3²=16.故选C.
∴AB²−AD²=BC²−CD²=(BD+CD)²−CD²=5²−3²=16.故选C.
3. (2024·广东佛山顺德区期末)如图,BD是Rt△ABC斜边AC上的中线. AB= 6,BC= 8,点P是BC上一个动点,过点P分别作AC和BD的垂线,垂足为E,F,则PE+PF的值是______.


答案:
4.8 [解析]如图,连接DP.
在Rt△ABC中,AB=6,BC=8,
∴AC²=AB²+BC²=6²+8²=100,
∴AC=10.

∵BD是斜边AC上的中线,
∴BD=CD=AD=$\frac{1}{2}$AC=5,
∴△BDC的面积=△ABD的面积=$\frac{1}{2}$△ABC的面积=$\frac{1}{2}$×$\frac{1}{2}$AB·BC=$\frac{1}{2}$×$\frac{1}{2}$×6×8=12.
∵PE⊥CD,PF⊥BD,且△BDP的面积+△CDP的面积=△BDC的面积,
∴$\frac{1}{2}$BD·PF+$\frac{1}{2}$CD·PE=12,
∴5PF+5PE=24,
∴PF+PE=4.8.
思路引导 连接DP,在Rt△ABC中,利用勾股定理,可求出AC=10,然后利用直角三角形斜边上的中线性质,可得BD=CD=AD=5,从而可得△BDC的面积=△ABD的面积=$\frac{1}{2}$△ABC的面积=12,最后根据△BDP的面积+△CDP的面积=△BDC的面积,进行计算即可解答。
4.8 [解析]如图,连接DP.
在Rt△ABC中,AB=6,BC=8,
∴AC²=AB²+BC²=6²+8²=100,
∴AC=10.

∵BD是斜边AC上的中线,
∴BD=CD=AD=$\frac{1}{2}$AC=5,
∴△BDC的面积=△ABD的面积=$\frac{1}{2}$△ABC的面积=$\frac{1}{2}$×$\frac{1}{2}$AB·BC=$\frac{1}{2}$×$\frac{1}{2}$×6×8=12.
∵PE⊥CD,PF⊥BD,且△BDP的面积+△CDP的面积=△BDC的面积,
∴$\frac{1}{2}$BD·PF+$\frac{1}{2}$CD·PE=12,
∴5PF+5PE=24,
∴PF+PE=4.8.
思路引导 连接DP,在Rt△ABC中,利用勾股定理,可求出AC=10,然后利用直角三角形斜边上的中线性质,可得BD=CD=AD=5,从而可得△BDC的面积=△ABD的面积=$\frac{1}{2}$△ABC的面积=12,最后根据△BDP的面积+△CDP的面积=△BDC的面积,进行计算即可解答。
4. (教材P89练习T2·变式)(2025·无锡期末)如图,以Rt△ACB的两边AB,BC为边向外作正方形的面积分别是$26 cm^2,10 cm^2,$则以另一边AC为直径向外作半圆的面积为$
2π
cm^2.$答案:2π [解析]
∵以Rt△ACB的两边AB,BC为边向外作正方形的面积分别是26cm²,10cm²,AC²=AB²−BC²,
∴AC²=26−10=16,
∴以另一边AC为直径向外作半圆的面积为$\frac{1}{2}$π×($\frac{AC}{2}$)²=$\frac{1}{2}$π×$\frac{16}{4}$=2π(cm²).
∵以Rt△ACB的两边AB,BC为边向外作正方形的面积分别是26cm²,10cm²,AC²=AB²−BC²,
∴AC²=26−10=16,
∴以另一边AC为直径向外作半圆的面积为$\frac{1}{2}$π×($\frac{AC}{2}$)²=$\frac{1}{2}$π×$\frac{16}{4}$=2π(cm²).
5. (2025·淮安期中)如图,在长方形ABCD中,AB= 8,AD= 10,E是AB边上一点,将△BCE沿直线CE折叠,点B的对应点F恰好落在边AD上,求AE的长.


答案:
∵四边形ABCD是长方形,将△BCE沿直线CE折叠,点B的对应点F恰好落在边AD上,
∴AB=CD=8,BC=AD=FC=10,
∴DF=$\sqrt{10²−8²}$=6,
∴AF=10−6=4.
设AE=x,则BE=FE=8−x,
在Rt△AEF中,
∵AE²+AF²=EF²,
∴x²+4²=(8−x)²,解得x=3,
∴AE=3.
∵四边形ABCD是长方形,将△BCE沿直线CE折叠,点B的对应点F恰好落在边AD上,
∴AB=CD=8,BC=AD=FC=10,
∴DF=$\sqrt{10²−8²}$=6,
∴AF=10−6=4.
设AE=x,则BE=FE=8−x,
在Rt△AEF中,
∵AE²+AF²=EF²,
∴x²+4²=(8−x)²,解得x=3,
∴AE=3.
6. 传统文化 《数书九章》(2023·南京中考)我国南宋数学家秦九韶的著作《数书九章》中有一道问题:“问沙田一段,有三斜,其小斜一十三里,中斜一十四里,大斜一十五里. 里法三百步,欲知为田几何?”问题大意:如图,在△ABC中,AB= 13里,BC= 14里,AC= 15里,则△ABC的面积是( ).

A.80平方里
B.82平方里
C.84平方里
D.86平方里

A.80平方里
B.82平方里
C.84平方里
D.86平方里
答案:
C [解析]如图,过点A作AD⊥BC于点D.
设BD=x里,则CD=(14−x)里.

在Rt△ABD中,AD²=13²−x²,
在Rt△ADC中,AD²=15²−(14−x)²,
∴13²−x²=15²−(14−x)²,解得x=5.
在Rt△ABD中,AD=$\sqrt{13²−5²}$=12(里),
∴△ABC的面积=$\frac{1}{2}$BC·AD=$\frac{1}{2}$×14×12=84(平方里).故选C.
归纳总结 本题考查了三角形的面积、勾股定理,解决本题的关键在于利用两个直角三角形的公共边找到突破点,主要利用了勾股定理。
C [解析]如图,过点A作AD⊥BC于点D.
设BD=x里,则CD=(14−x)里.

在Rt△ABD中,AD²=13²−x²,
在Rt△ADC中,AD²=15²−(14−x)²,
∴13²−x²=15²−(14−x)²,解得x=5.
在Rt△ABD中,AD=$\sqrt{13²−5²}$=12(里),
∴△ABC的面积=$\frac{1}{2}$BC·AD=$\frac{1}{2}$×14×12=84(平方里).故选C.
归纳总结 本题考查了三角形的面积、勾股定理,解决本题的关键在于利用两个直角三角形的公共边找到突破点,主要利用了勾股定理。
7. (苏州自主招生)我国古代伟大的数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式. 后人借助这种分割方法所得的图形证明了勾股定理,如图所示的长方形由两个这样的图形拼成,若a= 3,b= 4,则该长方形的面积为(
A.20
B.24
C.99/4
D.53/2
B
).A.20
B.24
C.99/4
D.53/2
答案:B [解析]设小正方形的边长为x,
∵a=3,b=4,
∴AB=3+4=7.
在Rt△ABC中,AC²+BC²=AB²,
即(3+x)²+(x+4)²=7²,
整理,得x²+7x−12=0,
而长方形面积为(x+3)(x+4)=x²+7x+12=12+12=24,
∴该长方形的面积为24.故选B
思路引导 欲求长方形的面积,则求出小正方形的边长即可,由此可设小正方形的边长为x,在直角三角形ABC中,利用勾股定理可建立关于x的方程,利用整体代入的思想解决问题,进而可求出该长方形的面积。
∵a=3,b=4,
∴AB=3+4=7.
在Rt△ABC中,AC²+BC²=AB²,
即(3+x)²+(x+4)²=7²,
整理,得x²+7x−12=0,
而长方形面积为(x+3)(x+4)=x²+7x+12=12+12=24,
∴该长方形的面积为24.故选B
思路引导 欲求长方形的面积,则求出小正方形的边长即可,由此可设小正方形的边长为x,在直角三角形ABC中,利用勾股定理可建立关于x的方程,利用整体代入的思想解决问题,进而可求出该长方形的面积。