8. 一个长为10 m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8 m,梯子的顶端下滑2 m后,底端将水平滑动2 m吗?请说明理由.
答案:
底端将滑动2m.理由如下:
如图,在Rt△ABC中,AB=10m,AC=8m,
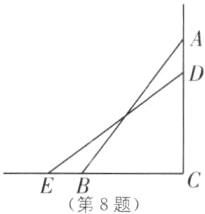
∴BC²=AB²−AC²=10²−8²=36,
∴BC=6m.
∵AD=2m,
∴CD=AC−AD=8−2=6(m).
在Rt△CDE中,DE=AB=10m,CD=6m,
∴CE²=DE²−CD²=10²−6²=64,
∴CE=8m,
∴EB=CE−BC=8−6=2(m).
故梯子底端将水平滑动2m.
底端将滑动2m.理由如下:
如图,在Rt△ABC中,AB=10m,AC=8m,

∴BC²=AB²−AC²=10²−8²=36,
∴BC=6m.
∵AD=2m,
∴CD=AC−AD=8−2=6(m).
在Rt△CDE中,DE=AB=10m,CD=6m,
∴CE²=DE²−CD²=10²−6²=64,
∴CE=8m,
∴EB=CE−BC=8−6=2(m).
故梯子底端将水平滑动2m.
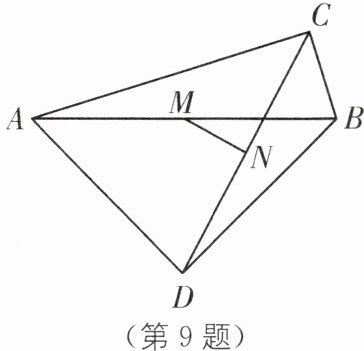
9. (2024·扬州邗江区期末)如图,∠ACB= ∠ADB= 90°,M,N分别是AB,CD的中点.
(1)求证:MN⊥CD;
(2)若AB= 50,CD= 48,求MN的长.
(1)求证:MN⊥CD;
(2)若AB= 50,CD= 48,求MN的长.

答案:
(1)连接MC,MD.
∵∠ACB=∠ADB=90°,M是AB的中点,
∴在Rt△ABC中,CM=$\frac{1}{2}$AB,在Rt△ABD中,DM=$\frac{1}{2}$AB,
∴MC=MD.
又N是CD的中点,
∴MN⊥CD.
(2)
∵AB=50,
∴MD=$\frac{1}{2}$×50=25.
∵CD=48,
∴ND=$\frac{1}{2}$×48=24.
又MN⊥CD,
∴在Rt△MND中,MN²=MD²−ND²=25²−24²=49,
∴MN=7.
(1)连接MC,MD.
∵∠ACB=∠ADB=90°,M是AB的中点,
∴在Rt△ABC中,CM=$\frac{1}{2}$AB,在Rt△ABD中,DM=$\frac{1}{2}$AB,
∴MC=MD.
又N是CD的中点,
∴MN⊥CD.
(2)
∵AB=50,
∴MD=$\frac{1}{2}$×50=25.
∵CD=48,
∴ND=$\frac{1}{2}$×48=24.
又MN⊥CD,
∴在Rt△MND中,MN²=MD²−ND²=25²−24²=49,
∴MN=7.
10. (2025·扬州江都区期中)如图,在Rt△ABC中,已知∠A= 90°,D是斜边BC的中点,DE⊥BC交AB于点E,连接CE.
(1)求证:$BE^{2}-AE^{2}= AC^{2}$;
(2)若AC= 6,BD= 5,求AE的长.

(1)求证:$BE^{2}-AE^{2}= AC^{2}$;
(2)若AC= 6,BD= 5,求AE的长.

答案:
(1)
∵DE⊥BC,D是斜边BC的中点,
∴DE是线段BC的垂直平分线,
∴BE=CE.
在Rt△ACE中,由勾股定理,得CE²=AC²+AE²,
∴BE²=AC²+AE²,
∴BE²−AE²=AC².
(2)
∵BD=5,D是斜边BC的中点,
∴BC=2BD=10.
在Rt△ABC中,由勾股定理,得AB=$\sqrt{BC²−AC²}$=$\sqrt{10²−6²}$=8,
∴AB=BE+AE=8.
设AE=x,则BE=CE=8−x,
在Rt△ACE中,由勾股定理得CE²=AC²+AE²,
即(8−x)²=6²+x²,解得x=$\frac{7}{4}$,
∴AE=$\frac{7}{4}$,即AE的长为$\frac{7}{4}$.
(1)
∵DE⊥BC,D是斜边BC的中点,
∴DE是线段BC的垂直平分线,
∴BE=CE.
在Rt△ACE中,由勾股定理,得CE²=AC²+AE²,
∴BE²=AC²+AE²,
∴BE²−AE²=AC².
(2)
∵BD=5,D是斜边BC的中点,
∴BC=2BD=10.
在Rt△ABC中,由勾股定理,得AB=$\sqrt{BC²−AC²}$=$\sqrt{10²−6²}$=8,
∴AB=BE+AE=8.
设AE=x,则BE=CE=8−x,
在Rt△ACE中,由勾股定理得CE²=AC²+AE²,
即(8−x)²=6²+x²,解得x=$\frac{7}{4}$,
∴AE=$\frac{7}{4}$,即AE的长为$\frac{7}{4}$.
11. 中考新考法 动点问题 (2025·无锡江阴期中)如图,在△ABC中,AB= 21 cm,AC= 17 cm,BC= 10 cm,点M从A点开始以2 cm/s的速度沿AB向B点运动,设出发的时间为t s.
(1)BM= ______(用含t的代数式表示).
(2)当t为何值时,△BCM为等腰三角形?
(3)当t= ______s时,点M在∠BCA的平分线上.
备用图

(1)BM= ______(用含t的代数式表示).
(2)当t为何值时,△BCM为等腰三角形?
(3)当t= ______s时,点M在∠BCA的平分线上.
备用图

答案:
(1)(21−2t)cm
(2)如图
(1),过点C,作CH⊥AB于点H,
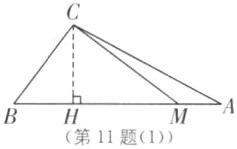
设BH=xcm,则AH=(21−x)cm,
由勾股定理可得,BC²−BH²=AC²−AH²,
∵AB=21cm,AC=17cm,BC=10cm,
∴10²−x²=17²−(21−x)²,
∴x=6,
∴BH=6,
∴CH=$\sqrt{BC²−BH²}$=8.
①当BM=BC时,21−2t=10,
∴t=$\frac{11}{2}$;
②当BC=CM时,BM=2BH=12,
∴21−2t=12,
∴t=$\frac{9}{2}$;
③当BM=CM时,
∵BH=6cm,
∴AH=AB−BH=21−6=15(cm),
∴MH=AH−AM=(15−2t)cm.
∵CM²=MH²+CH²,
∴(15−2t)²+8²=(21−2t)²,
∴t=$\frac{19}{3}$.
综上所述,当t的值是$\frac{11}{2}$或$\frac{9}{2}$或$\frac{19}{3}$时,△BCM为等腰三角形。
(3)$\frac{119}{18}$ [解析]如图
(2),点M在∠BCA的平分线上,过点M作MD⊥BC,ME⊥AC于点D,E,
∴MD=ME.

由
(2)知CH=8cm,
∵三角形ABC的面积=三角形BCM的面积+三角形ACM的面积,
∴$\frac{1}{2}$AB·CH=$\frac{1}{2}$BC·DM+$\frac{1}{2}$AC·ME,
∴$\frac{1}{2}$×21×8=$\frac{1}{2}$×10ME+$\frac{1}{2}$×17ME,
∴ME=$\frac{56}{9}$.
∵三角形AMC的面积=$\frac{1}{2}$AM·CH=$\frac{1}{2}$AC·ME,
∴2t×8=17×$\frac{56}{9}$,
∴t=$\frac{119}{18}$.
(1)(21−2t)cm
(2)如图
(1),过点C,作CH⊥AB于点H,

设BH=xcm,则AH=(21−x)cm,
由勾股定理可得,BC²−BH²=AC²−AH²,
∵AB=21cm,AC=17cm,BC=10cm,
∴10²−x²=17²−(21−x)²,
∴x=6,
∴BH=6,
∴CH=$\sqrt{BC²−BH²}$=8.
①当BM=BC时,21−2t=10,
∴t=$\frac{11}{2}$;
②当BC=CM时,BM=2BH=12,
∴21−2t=12,
∴t=$\frac{9}{2}$;
③当BM=CM时,
∵BH=6cm,
∴AH=AB−BH=21−6=15(cm),
∴MH=AH−AM=(15−2t)cm.
∵CM²=MH²+CH²,
∴(15−2t)²+8²=(21−2t)²,
∴t=$\frac{19}{3}$.
综上所述,当t的值是$\frac{11}{2}$或$\frac{9}{2}$或$\frac{19}{3}$时,△BCM为等腰三角形。
(3)$\frac{119}{18}$ [解析]如图
(2),点M在∠BCA的平分线上,过点M作MD⊥BC,ME⊥AC于点D,E,
∴MD=ME.

由
(2)知CH=8cm,
∵三角形ABC的面积=三角形BCM的面积+三角形ACM的面积,
∴$\frac{1}{2}$AB·CH=$\frac{1}{2}$BC·DM+$\frac{1}{2}$AC·ME,
∴$\frac{1}{2}$×21×8=$\frac{1}{2}$×10ME+$\frac{1}{2}$×17ME,
∴ME=$\frac{56}{9}$.
∵三角形AMC的面积=$\frac{1}{2}$AM·CH=$\frac{1}{2}$AC·ME,
∴2t×8=17×$\frac{56}{9}$,
∴t=$\frac{119}{18}$.