1. (2024·成都中考)在平面直角坐标系 xOy 中,点 P(1,-4)关于原点对称的点的坐标是(
A.(-1,-4)
B.(-1,4)
C.(1,4)
D.(1,-4)
B
).A.(-1,-4)
B.(-1,4)
C.(1,4)
D.(1,-4)
答案:B [解析] 点P(1,−4)关于原点对称的点的坐标是(−1,4).故选B.
2. (2023·常州中考)在平面直角坐标系中,若点 P 的坐标为(2,1),则点 P 关于 y 轴对称的点的坐标为(
A.(-2,-1)
B.(2,-1)
C.(-2,1)
D.(2,1)
C
).A.(-2,-1)
B.(2,-1)
C.(-2,1)
D.(2,1)
答案:C [解析] 点P的坐标是(2,1),则点P关于y轴对称的点的坐标是(−2,1).故选C.
3. (教材 P121 例 1·变式)(2023·绍兴中考)在平面直角坐标系中,将点(m,n)先向右平移 2 个单位,再向上平移 1 个单位,最后所得点的坐标是(
A.(m-2,n-1)
B.(m-2,n+1)
C.(m+2,n-1)
D.(m+2,n+1)
D
).A.(m-2,n-1)
B.(m-2,n+1)
C.(m+2,n-1)
D.(m+2,n+1)
答案:D [解析] 将点(m,n)先向右平移2个单位,再向上平移1个单位,最后所得点的坐标是(m+2,n+1).故选D.
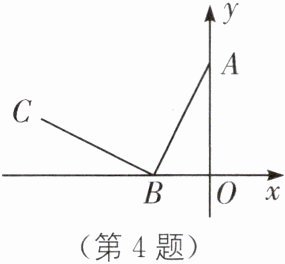
4. 一线三等角模型 (2025·盐城射阳实验中学月考)如图,在平面直角坐标系中,A(0,4),B(-2,0),线段 BC 是由线段 BA 绕点 B 逆时针旋转 90°而得到的,则点 C 的坐标是______.

答案:
(−6,2) [解析] 如图,过点C作CM⊥x轴于点M,则∠CMB=90°,
∵A(0,4),B(−2,0),
∴OB=2,OA=4.
∵线段BC是由线段BA绕点B 逆时针旋转90°而得到,
∴∠CMB=∠ABC=∠AOB=90°,BC=BA,
∴∠ABO+∠OAB=90°,∠ABO+∠CBM=90°,
∴∠OAB=∠CBM,
∴△BCM≌△ABO,
∴BM=AO=4,CM=OB=2,
∴OM=BM+OB=6.
∵点C在第二象限,
∴C(−6,2).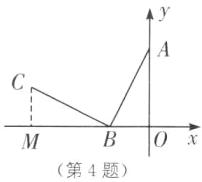
(−6,2) [解析] 如图,过点C作CM⊥x轴于点M,则∠CMB=90°,
∵A(0,4),B(−2,0),
∴OB=2,OA=4.
∵线段BC是由线段BA绕点B 逆时针旋转90°而得到,
∴∠CMB=∠ABC=∠AOB=90°,BC=BA,
∴∠ABO+∠OAB=90°,∠ABO+∠CBM=90°,
∴∠OAB=∠CBM,
∴△BCM≌△ABO,
∴BM=AO=4,CM=OB=2,
∴OM=BM+OB=6.
∵点C在第二象限,
∴C(−6,2).

5. (教材 P123 例 2·拓展)在平面直角坐标系中,已知点 A(x-3,y+2)与点 B(5,3y-2).
(1)若点 A 与点 B 关于 x 轴对称,求 x+y 的值;
(2)若 AB//x 轴,且 AB= 2,求点 A 的坐标.
精题详解
(1)若点 A 与点 B 关于 x 轴对称,求 x+y 的值;
(2)若 AB//x 轴,且 AB= 2,求点 A 的坐标.
精题详解
答案:
(1)
∵点A与点B关于x轴对称,
∴x−3=5,(y+2)+(3y−2)=0,
∴x=8,y=0,
∴x+y=8+0=8.
(2)当点A在点B的右边时,
∵AB//x轴,且AB=2,
∴点A的横坐标是7,y+2=3y−2,
∴y=2,
∴A(7,4);当点A在点B的左边时,
∵AB//x轴,且AB=2,
∴点A的横坐标是3,纵坐标还是4,则A(3,4).综上所述,点A的坐标为(3,4)或(7,4). 归纳总结 本题考查了关于x轴对称的点的坐标,熟练掌握对称点的特点是解题的关键.
(1)
∵点A与点B关于x轴对称,
∴x−3=5,(y+2)+(3y−2)=0,
∴x=8,y=0,
∴x+y=8+0=8.
(2)当点A在点B的右边时,
∵AB//x轴,且AB=2,
∴点A的横坐标是7,y+2=3y−2,
∴y=2,
∴A(7,4);当点A在点B的左边时,
∵AB//x轴,且AB=2,
∴点A的横坐标是3,纵坐标还是4,则A(3,4).综上所述,点A的坐标为(3,4)或(7,4). 归纳总结 本题考查了关于x轴对称的点的坐标,熟练掌握对称点的特点是解题的关键.
6. (教材 P124 探究·拓展)如图,将△ABC 先向右平移 1 个单位,再绕点 P 按顺时针方向旋转 90°,得到△A'B'C',则点 B 的对应点 B'的坐标是( ).

A.(4,0)
B.(2,-2)
C.(4,-1)
D.(2,-3)

A.(4,0)
B.(2,-2)
C.(4,-1)
D.(2,-3)
答案:
C [解析] 作出旋转后的图形△A'B'C'如下:
∴点B'的坐标为(4,−1).故选C.
C [解析] 作出旋转后的图形△A'B'C'如下:

∴点B'的坐标为(4,−1).故选C.
7. (山东淄博张店七中自主招生)点 A(4,3)经过某种图形变化后得到点 B(-3,4),这种图形变化可以是( ).
A.关于 x 轴对称
B.关于 y 轴对称
C.绕原点逆时针旋转 90°
D.绕原点顺时针旋转 90°
A.关于 x 轴对称
B.关于 y 轴对称
C.绕原点逆时针旋转 90°
D.绕原点顺时针旋转 90°
答案:
C [解析] 如图,观察图形可知,点A绕点O逆时针旋转90°得到点B. 故选C.
故选C.
C [解析] 如图,观察图形可知,点A绕点O逆时针旋转90°得到点B.
 故选C.
故选C.8. 如图,平面直角坐标系中,点 B 在第一象限,点 A 在 x 轴的正半轴上,∠AOB= ∠B= 30°,OA= 2. 将△AOB 绕点 O 逆时针旋转 90°,点 B 的对应点 B'的坐标是( ).

A.($-\sqrt{3}$,3)
B.(-3,$\sqrt{3}$)
C.($-\sqrt{3}$,2+$\sqrt{3}$)
D.(-1,2+$\sqrt{3}$)

A.($-\sqrt{3}$,3)
B.(-3,$\sqrt{3}$)
C.($-\sqrt{3}$,2+$\sqrt{3}$)
D.(-1,2+$\sqrt{3}$)
答案:
A [解析] 如图,过点B'作B'H⊥y轴于点H. 在Rt△A'B'H中,
在Rt△A'B'H中,
∵A'B'=2,∠B'A'H=60°,
∴A'H=1,由直角三角形的性质可得含30°角的直角三角形,较短直角边长等于斜边长的一半。B'H= $\sqrt{A'B'² - A'H²}$ = $\sqrt{2² - 1²}$ = √3,
∴OH=2 + 1 = 3,
∴B'( - √3,3).故选A.
A [解析] 如图,过点B'作B'H⊥y轴于点H.
 在Rt△A'B'H中,
在Rt△A'B'H中,∵A'B'=2,∠B'A'H=60°,
∴A'H=1,由直角三角形的性质可得含30°角的直角三角形,较短直角边长等于斜边长的一半。B'H= $\sqrt{A'B'² - A'H²}$ = $\sqrt{2² - 1²}$ = √3,
∴OH=2 + 1 = 3,
∴B'( - √3,3).故选A.