9. (内蒙古包头自主招生)已知点 M(3,-2),它与点 N(x,y)在同一条平行于 x 轴的直线上,且 MN= 4,那么点 N 的坐标是(
A.(7,-2)或(-1,-2)
B.(3,2)或(3,-6)
C.(7,2)或(-1,-6)
D.(4,-2)或(-4,-2)
A
).A.(7,-2)或(-1,-2)
B.(3,2)或(3,-6)
C.(7,2)或(-1,-6)
D.(4,-2)或(-4,-2)
答案：A [解析]
∵点M(3,−2),MN//x轴,
∴点N的纵坐标y=−2,点N在点M的左边时，点N的横坐标为3−4=−1;点N在点M的右边时，点N的横坐标为3+4=7,所以点N的坐标为(7,−2)或(−1,−2).故选A.
∵点M(3,−2),MN//x轴,
∴点N的纵坐标y=−2,点N在点M的左边时，点N的横坐标为3−4=−1;点N在点M的右边时，点N的横坐标为3+4=7,所以点N的坐标为(7,−2)或(−1,−2).故选A.
10. (2025·连云港期末)已知点 P₁(a,-3)和 P₂(-2,b)关于 y 轴对称,则$(a+b)^{2025}$的值为(
A.0
B.-1
C.1
D.$(-3)^{2025}$
B
).A.0
B.-1
C.1
D.$(-3)^{2025}$
答案：B [解析]
∵点P₁(a,−3)和P₂(−2,b)关于y轴对称,
∴a=2,b=−3,
∴(a+b)²⁰²⁵=(2−3)²⁰²⁵=−1.故选B.
∵点P₁(a,−3)和P₂(−2,b)关于y轴对称,
∴a=2,b=−3,
∴(a+b)²⁰²⁵=(2−3)²⁰²⁵=−1.故选B.
11. (2023·湘西州中考)在平面直角坐标系中,已知点 P(a,1)与点 Q(2,b)关于 x 轴对称,则 a+b=
1
.答案：1 [解析]
∵点P(a,1)与点Q(2,b)关于x轴对称,
∴点P(a,1)与点Q(2,b)的横坐标相同,纵坐标互为相反数,
∴a=2,1+b=0,解得b=−1,
∴a+b=1. 归纳总结 本题考查了关于x轴对称的两点的坐标之间的关系，属于基础题，明白关于x轴对称的点横坐标相同，纵坐标互为相反数是解题关键.
∵点P(a,1)与点Q(2,b)关于x轴对称,
∴点P(a,1)与点Q(2,b)的横坐标相同,纵坐标互为相反数,
∴a=2,1+b=0,解得b=−1,
∴a+b=1. 归纳总结 本题考查了关于x轴对称的两点的坐标之间的关系，属于基础题，明白关于x轴对称的点横坐标相同，纵坐标互为相反数是解题关键.
12. 如图,在正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,△ABC 的三个顶点坐标分别为 A(1,-1),B(2,-5),C(5,-4).
(1)将△ABC 先向左平移 6 个单位,再向上平移 4 个单位,得到$△A_1B_1C_1,$画出两次平移后的$△A_1B_1C_1,$并写出点$ A_1$的坐标；
(2)画出$△A_1B_1C_1$绕点$ C_1$顺时针旋转 90°后得到的$△A_2B_2C_1,$并写出点$ A_2$的坐标；
(3)求△ABC 的面积.
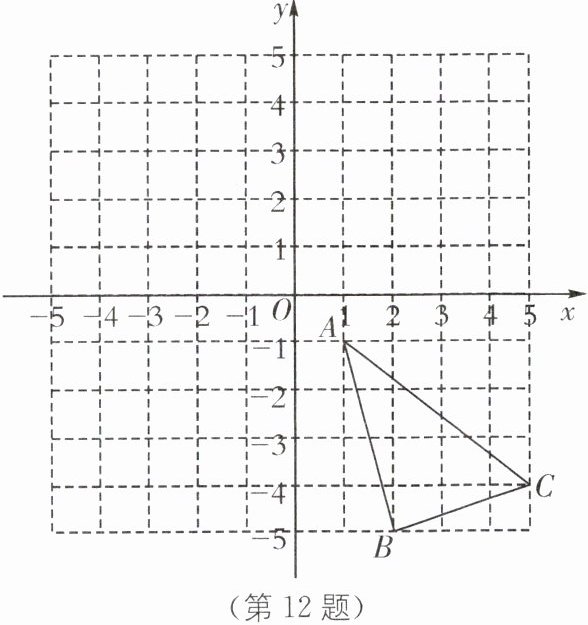
(1)将△ABC 先向左平移 6 个单位,再向上平移 4 个单位,得到$△A_1B_1C_1,$画出两次平移后的$△A_1B_1C_1,$并写出点$ A_1$的坐标；
(2)画出$△A_1B_1C_1$绕点$ C_1$顺时针旋转 90°后得到的$△A_2B_2C_1,$并写出点$ A_2$的坐标；
(3)求△ABC 的面积.
答案：
(1)如图,△A₁B₁C₁即为所求,点A₁的坐标为(−5,3).
(2)如图,△A₂B₂C₁即为所求,点A₂的坐标为(2,4).
(3)△ABC的面积为4×4 - $\frac{1}{2}$×4×3 - $\frac{1}{2}$×4×1 - $\frac{1}{2}$×3×1 = 16 - 6 - 2 - $\frac{3}{2}$ = $\frac{13}{2}$.
归纳总结 本题考查作图——平移变换、旋转变换，解题的关键是掌握平移变换、旋转变换的性质，属于中考常考题型.
(1)如图,△A₁B₁C₁即为所求,点A₁的坐标为(−5,3).
(2)如图,△A₂B₂C₁即为所求,点A₂的坐标为(2,4).
(3)△ABC的面积为4×4 - $\frac{1}{2}$×4×3 - $\frac{1}{2}$×4×1 - $\frac{1}{2}$×3×1 = 16 - 6 - 2 - $\frac{3}{2}$ = $\frac{13}{2}$.
归纳总结 本题考查作图——平移变换、旋转变换，解题的关键是掌握平移变换、旋转变换的性质，属于中考常考题型.13. 动点问题 中考新考法 动点问题 如图,点 A(1,0),B 在 y 轴上,将△OAB 沿 x 轴负方向平移,平移后的图形为△DEC,且点 C 的坐标为(-3,2).
(1)直接写出点 E 的坐标为______.
(2)在四边形 ABCD 中,点 P 从点 B 出发,沿 BC→CD 移动. 若点 P 的速度为每秒 1 个单位长度,运动时间为 t 秒,回答下列问题：
①当 t= ______秒时,点 P 的横坐标与纵坐标互为相反数.
②求点 P 在运动过程中的坐标(用含 t 的式子表示,写出过程).
③当 3＜t＜5 时,设∠CBP= x°,∠PAD= y°,∠BPA= z°,试问 x,y,z 之间的数量关系能否确定？若能,请用含 x,y 的式子表示 z,写出过程；若不能,说明理由.
精题详解
(1)直接写出点 E 的坐标为______.
(2)在四边形 ABCD 中,点 P 从点 B 出发,沿 BC→CD 移动. 若点 P 的速度为每秒 1 个单位长度,运动时间为 t 秒,回答下列问题：
①当 t= ______秒时,点 P 的横坐标与纵坐标互为相反数.
②求点 P 在运动过程中的坐标(用含 t 的式子表示,写出过程).
③当 3＜t＜5 时,设∠CBP= x°,∠PAD= y°,∠BPA= z°,试问 x,y,z 之间的数量关系能否确定？若能,请用含 x,y 的式子表示 z,写出过程；若不能,说明理由.
精题详解
答案：
(1)(−2,0)
(2)①2 [解析]
∵点C的坐标为(−3,2),
∴BC=3,CD=2.
∵点P的横坐标与纵坐标互为相反数,
∴点P在线段BC上,
∴PB=CD,即t=2,
∴当t=2秒时,点P的横坐标与纵坐标互为相反数. ②当点P在线段BC上时,点P的坐标为(−t,2);当点P在线段CD上时,点P的坐标为(−3,5−t). ③能确定,z=x+y.理由如下:如图,过点P作PF//BC交AB于点F,则PF//AD,
∴∠1=∠CBP=x°,∠2=∠DAP=y°,
∴∠BPA=∠1+∠2=x°+y°=z°,
∴z=x+y.
(1)(−2,0)
(2)①2 [解析]
∵点C的坐标为(−3,2),
∴BC=3,CD=2.
∵点P的横坐标与纵坐标互为相反数,
∴点P在线段BC上,
∴PB=CD,即t=2,
∴当t=2秒时,点P的横坐标与纵坐标互为相反数. ②当点P在线段BC上时,点P的坐标为(−t,2);当点P在线段CD上时,点P的坐标为(−3,5−t). ③能确定,z=x+y.理由如下:如图,过点P作PF//BC交AB于点F,则PF//AD,
∴∠1=∠CBP=x°,∠2=∠DAP=y°,
∴∠BPA=∠1+∠2=x°+y°=z°,
∴z=x+y.