1. 已知y与x成正比例,且当x= 2时,y= 3,则当y= 2时,x的值为(
A.$\frac{3}{4}$
B.$\frac{4}{3}$
C.$\frac{3}{2}$
D.3
B
).A.$\frac{3}{4}$
B.$\frac{4}{3}$
C.$\frac{3}{2}$
D.3
答案:B 解析 设y=kx,当x=2时,y=3,代入,得2k=3,解得k= $\frac{3}{2}$,所以此函数的表达式为y= $\frac{3}{2}$x,所以当y=2时,即2= $\frac{3}{2}$x,解得x= $\frac{4}{3}$.故选B.
2. (2024·无锡宜兴一模)若一次函数$y= 2x+1的图象经过点(-3,y_1),(4,y_2)$,则$y_1与y_2$的大小关系是(
A.$y_1<y_2$
B.$y_1>y_2$
C.$y_1\leq y_2$
D.$y_1\geq y_2$
A
).A.$y_1<y_2$
B.$y_1>y_2$
C.$y_1\leq y_2$
D.$y_1\geq y_2$
答案:A 解析
∵一次函数y=2x+1的图象过点(-3,y₁),(4,y₂),
∴y₁=-5,y₂=9,
∴y₁<y₂.故选A.
∵一次函数y=2x+1的图象过点(-3,y₁),(4,y₂),
∴y₁=-5,y₂=9,
∴y₁<y₂.故选A.
3. 已知一次函数$y= -x+b$,当$x= 1$时,$y= 2$,则$b= $
3
.答案:3 解析
∵一次函数y=-x+b,当x=1时,y=2,
∴2=-1+b,解得b=3.
∵一次函数y=-x+b,当x=1时,y=2,
∴2=-1+b,解得b=3.
4. 张老师带领x名学生到某动物园参观,已知成人票每张10元,学生票每张5元,设门票的总费用为y元,则$y=$
5x+10
.答案:5x+10
解析:
$5x + 10$
5. 跨学科 弹簧长度与所挂物体质量的关系 物理实验证实:在弹性限度内,某弹簧长度y(cm)与所挂物体质量x(kg)满足函数关系$y= kx+15$.下表是测量物体质量时,该弹簧长度与所挂物体质量的数量关系.
| x | 0 | 2 | 5 |
| y | 15 | 19 | 25 |
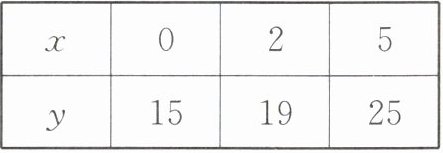
(1)求y与x的函数表达式;
(2)当弹簧长度为20 cm时,求所挂物体的质量.
| x | 0 | 2 | 5 |
| y | 15 | 19 | 25 |

(1)求y与x的函数表达式;
(2)当弹簧长度为20 cm时,求所挂物体的质量.
答案:
(1)把x=2,y=19代入y=kx+15,得19=2k+15,解得k=2,所以y与x的函数表达式为y=2x+15(x≥0).
(2)把y=20代入y=2x+15,得20=2x+15,解得x=2.5.故所挂物体的质量为2.5 kg.
(1)把x=2,y=19代入y=kx+15,得19=2k+15,解得k=2,所以y与x的函数表达式为y=2x+15(x≥0).
(2)把y=20代入y=2x+15,得20=2x+15,解得x=2.5.故所挂物体的质量为2.5 kg.
6. 教材P148练习T2·变式 (2024·大连二模)汽车在公路上行驶时,油箱中剩余油量y(单位:L)是行驶里程x(单位:km)的函数,小丽记录了一次远行时汽车行驶里程及油箱中剩余的油量,数据如表:
| 行驶里程x/km | 0 | 100 | 200 | 300 |
| 剩余油量y/L | 50 | 40 | 30 | 20 |

该函数的表达式是(
A.$y= 0.4x$
B.$y= -0.1x+50$
C.$y= \frac{4000}{x}$
D.$y= \frac{1}{250}x^2+50$
| 行驶里程x/km | 0 | 100 | 200 | 300 |
| 剩余油量y/L | 50 | 40 | 30 | 20 |

该函数的表达式是(
B
).A.$y= 0.4x$
B.$y= -0.1x+50$
C.$y= \frac{4000}{x}$
D.$y= \frac{1}{250}x^2+50$
答案:B 解析
∵100-0=200-100=300-200,40-50=30-40=20-30,
∴y与x成一次函数关系.设油箱中剩余油量y(单位:L)关于行驶里程x(单位:km)的函数表达式为y=kx+b,将(0,50),(100,40)代入y=kx+b,得 $\begin{cases} b=50, \\ 100k+b=40, \end{cases}$ 解得 $\begin{cases} k=-0.1, \\ b=50, \end{cases}$
∴该函数的表达式是y=-0.1x+50.故选B.
∵100-0=200-100=300-200,40-50=30-40=20-30,
∴y与x成一次函数关系.设油箱中剩余油量y(单位:L)关于行驶里程x(单位:km)的函数表达式为y=kx+b,将(0,50),(100,40)代入y=kx+b,得 $\begin{cases} b=50, \\ 100k+b=40, \end{cases}$ 解得 $\begin{cases} k=-0.1, \\ b=50, \end{cases}$
∴该函数的表达式是y=-0.1x+50.故选B.
7. (2024·盐城景山中学期中)已知y与$x-2$成正比例,且当$x= 1$时,$y= -2$,则y与x的函数表达式是______
y=2x-4
.答案:y=2x-4 解析 设y与x-2的函数表达式是y=k(x-2),将x=1,y=-2代入,解得k=2,
∴y与x的函数表达式是y=2x-4.
∴y与x的函数表达式是y=2x-4.
8. (2025·宿迁期末)如图,已知B中的实数与A中的实数之间的对应关系是某个一次函数.
(1)若用y表示B中的实数,用x表示A中的实数,求y与x之间的函数表达式;
(2)求$m+n$的值.

(1)若用y表示B中的实数,用x表示A中的实数,求y与x之间的函数表达式;
(2)求$m+n$的值.

答案:
(1)设一次函数的表达式为y=kx+b,由题意,得 $\begin{cases} -3k+b=9, \\ b=-3, \end{cases}$ 解得 $\begin{cases} k=-4, \\ b=-3. \end{cases}$ 故一次函数的表达式为y=-4x-3.
(2)在函数y=-4x-3中,当x=-1时,n=1;当y=5时,m=-2,
∴m+n=-2+1=-1.
(1)设一次函数的表达式为y=kx+b,由题意,得 $\begin{cases} -3k+b=9, \\ b=-3, \end{cases}$ 解得 $\begin{cases} k=-4, \\ b=-3. \end{cases}$ 故一次函数的表达式为y=-4x-3.
(2)在函数y=-4x-3中,当x=-1时,n=1;当y=5时,m=-2,
∴m+n=-2+1=-1.