7. 已知柱体的体积$V = S\cdot h$,其中S表示柱体的底面积,h表示柱体的高.如图,现将长方形ABCD绕直线l旋转一周,则形成的几何体的体积等于 (
A.$πr^{2}h$
B.$2πr^{2}h$
C.$3πr^{2}h$
D.$4πr^{2}h$
C
)A.$πr^{2}h$
B.$2πr^{2}h$
C.$3πr^{2}h$
D.$4πr^{2}h$
答案:C
解析:
解:由图可知,长方形ABCD的长为h,宽为2r - r = r。
绕直线l旋转一周后,形成的几何体是一个大圆柱挖去一个同高的小圆柱。
大圆柱底面半径为2r,高为h,体积$V_{大} = π(2r)^{2}h = 4πr^{2}h$。
小圆柱底面半径为r,高为h,体积$V_{小} = πr^{2}h$。
所求几何体体积$V = V_{大} - V_{小} = 4πr^{2}h - πr^{2}h = 3πr^{2}h$。
答案:C
绕直线l旋转一周后,形成的几何体是一个大圆柱挖去一个同高的小圆柱。
大圆柱底面半径为2r,高为h,体积$V_{大} = π(2r)^{2}h = 4πr^{2}h$。
小圆柱底面半径为r,高为h,体积$V_{小} = πr^{2}h$。
所求几何体体积$V = V_{大} - V_{小} = 4πr^{2}h - πr^{2}h = 3πr^{2}h$。
答案:C
8. 如图,在长方形ABCD中,$AB = 3$,$BC = 4$,把长方形绕着它的一边所在的直线旋转一周,所形成的几何体的体积为
$ 48\pi $ 或 $ 36\pi $
.答案:$ 48\pi $ 或 $ 36\pi $
解析:
情况一:绕AB所在直线旋转一周
底面半径$r=BC=4$,高$h=AB=3$
体积$V=πr^{2}h=π×4^{2}×3=48π$
情况二:绕BC所在直线旋转一周
底面半径$r=AB=3$,高$h=BC=4$
体积$V=πr^{2}h=π×3^{2}×4=36π$
$48π$或$36π$
底面半径$r=BC=4$,高$h=AB=3$
体积$V=πr^{2}h=π×4^{2}×3=48π$
情况二:绕BC所在直线旋转一周
底面半径$r=AB=3$,高$h=BC=4$
体积$V=πr^{2}h=π×3^{2}×4=36π$
$48π$或$36π$
9. 如图①,将边长为8cm的正方形纸片做成七巧板,并用这副七巧板拼成“温暖小屋”(如图②),则图中阴影部分的面积是
$ 16cm^{2} $
.答案:$ 16cm^{2} $
解析:
解:正方形边长为8cm,面积为$8×8 = 64cm^{2}$。
七巧板中,阴影部分由一个小正方形和一个平行四边形组成。小正方形面积为原正方形面积的$\frac{1}{8}$,平行四边形面积也为原正方形面积的$\frac{1}{8}$。
阴影部分面积为$64×\frac{1}{8} + 64×\frac{1}{8} = 8 + 8 = 16cm^{2}$。
$16cm^{2}$
七巧板中,阴影部分由一个小正方形和一个平行四边形组成。小正方形面积为原正方形面积的$\frac{1}{8}$,平行四边形面积也为原正方形面积的$\frac{1}{8}$。
阴影部分面积为$64×\frac{1}{8} + 64×\frac{1}{8} = 8 + 8 = 16cm^{2}$。
$16cm^{2}$
10. 如图,图(1),图(2),图(3),图(4),图(5)中的图形②是由图形①经过翻折、平移或旋转这三种变换得到的,请分别指出它们是由其中哪一种变换得到的.
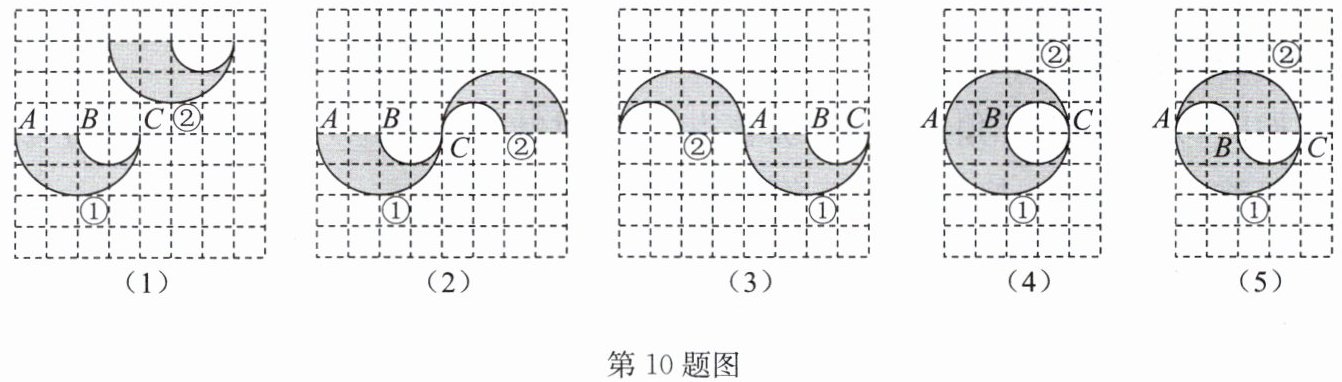

答案:解: 题图(1)中的图形②是由图形①经过平移变换而得到的;
题图(2)中的图形②是由图形①经过旋转变换而得到的(绕点 C 旋转 $ 180^{\circ} $);
题图(3)中的图形②是由图形①经过旋转变换而得到的(绕点 A 旋转 $ 180^{\circ} $);
题图(4)中的图形②是由图形①经过翻折变换而得到的(以 AC 所在的直线为轴);
题图(5)中的图形②是由图形①经过旋转变换而得到的(绕点 B 旋转 $ 180^{\circ} $).
题图(2)中的图形②是由图形①经过旋转变换而得到的(绕点 C 旋转 $ 180^{\circ} $);
题图(3)中的图形②是由图形①经过旋转变换而得到的(绕点 A 旋转 $ 180^{\circ} $);
题图(4)中的图形②是由图形①经过翻折变换而得到的(以 AC 所在的直线为轴);
题图(5)中的图形②是由图形①经过旋转变换而得到的(绕点 B 旋转 $ 180^{\circ} $).
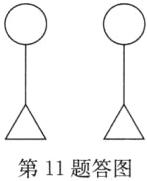
11. 以给定的图形“○○,△△,=”(两个圆、两个三角形、两条平行线段)为构件,构思独特且有意义的图形.举例:如图,左框中是符合要求的一个图形.你还能构思出其他的图形吗? 请在右框中画出与之不同的一个图形,并写出一两句贴切、诙谐的解说词.


答案:
解:如答图所示,解说词:两把铲子.(答案不唯一)
解:如答图所示,解说词:两把铲子.(答案不唯一)
