6.小明用如图所示的纸板折成了一个正方体的盒子,里面装了一瓶墨水,与其他三个空盒子混放在一起,观察四个选项,可知墨水瓶所在的盒子是 (
B
)答案:B
解析:
通过观察正方体展开图可知,带圆形的面与两个阴影三角形面不相邻,与空白三角形面也不相邻。分析各选项:
A选项中圆形面与阴影三角形面相邻,不符合;
C选项中圆形面与阴影三角形面相邻,不符合;
D选项中圆形面与空白三角形面相邻,不符合;
B选项中可见面均为阴影三角形面和空白面,无圆形面,符合圆形面与各三角形面不相邻的特征。
B
A选项中圆形面与阴影三角形面相邻,不符合;
C选项中圆形面与阴影三角形面相邻,不符合;
D选项中圆形面与空白三角形面相邻,不符合;
B选项中可见面均为阴影三角形面和空白面,无圆形面,符合圆形面与各三角形面不相邻的特征。
B
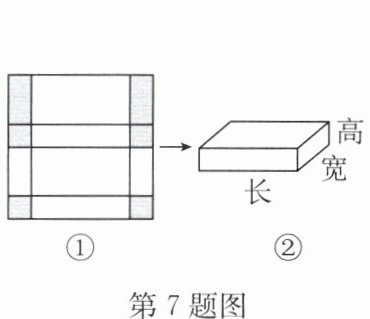
7.如图①是边长为18 cm的正方形纸板,截掉阴影部分后将其折叠成如图②所示的长方体盒子.已知该长方体的宽是高的2倍,则它的体积是
216
$cm^3.$
答案:216
解析:
设长方体的高为 $ x $ cm,则宽为 $ 2x $ cm。
由题意,正方形纸板边长为18 cm,折叠后长方体的长为 $ 18 - 2x $ cm,宽满足 $ 2x + 2x = 18 $(即折叠后两个高与两个宽之和等于正方形边长)。
解方程 $ 4x = 18 $,得 $ x = 4.5 $。
则宽为 $ 2x = 9 $ cm,长为 $ 18 - 2x = 9 $ cm。
体积 $ V = 长 × 宽 × 高 = 9 × 9 × 4.5 = 364.5 $(此步骤错误,重新分析)
正确分析:
设长方体的高为 $ x $ cm,则宽为 $ 2x $ cm。
由折叠过程可知,正方形纸板的边长等于长方体的两个高加两个宽,即 $ 2x + 2 × 2x = 18 $(应为:长方体的宽由折叠后两个高组成,长由正方形边长减去两个高组成,宽为 $ 2x $,则 $ 2x + 2x = 18 $ 错误,正确应为:长方体的底面长方形,其周长相关折叠关系为:正方形的边长等于长方体的高的两倍加上长方体的长,同时长方体的宽等于(正方形边长减去两倍高)的一半。即宽 $ 2x = \frac{18 - 2x}{2} $)
解方程 $ 2x = \frac{18 - 2x}{2} $:
$ 4x = 18 - 2x $
$ 6x = 18 $
$ x = 3 $
则宽为 $ 2x = 6 $ cm,长为 $ 18 - 2x = 12 $ cm。
体积 $ V = 12 × 6 × 3 = 216 $ $ cm^3 $。
答案:216
由题意,正方形纸板边长为18 cm,折叠后长方体的长为 $ 18 - 2x $ cm,宽满足 $ 2x + 2x = 18 $(即折叠后两个高与两个宽之和等于正方形边长)。
解方程 $ 4x = 18 $,得 $ x = 4.5 $。
则宽为 $ 2x = 9 $ cm,长为 $ 18 - 2x = 9 $ cm。
体积 $ V = 长 × 宽 × 高 = 9 × 9 × 4.5 = 364.5 $(此步骤错误,重新分析)
正确分析:
设长方体的高为 $ x $ cm,则宽为 $ 2x $ cm。
由折叠过程可知,正方形纸板的边长等于长方体的两个高加两个宽,即 $ 2x + 2 × 2x = 18 $(应为:长方体的宽由折叠后两个高组成,长由正方形边长减去两个高组成,宽为 $ 2x $,则 $ 2x + 2x = 18 $ 错误,正确应为:长方体的底面长方形,其周长相关折叠关系为:正方形的边长等于长方体的高的两倍加上长方体的长,同时长方体的宽等于(正方形边长减去两倍高)的一半。即宽 $ 2x = \frac{18 - 2x}{2} $)
解方程 $ 2x = \frac{18 - 2x}{2} $:
$ 4x = 18 - 2x $
$ 6x = 18 $
$ x = 3 $
则宽为 $ 2x = 6 $ cm,长为 $ 18 - 2x = 12 $ cm。
体积 $ V = 12 × 6 × 3 = 216 $ $ cm^3 $。
答案:216
8.如图为一个长方体的表面展开图,且长方体的底面为正方形.根据图中标示的长度,则此长方体的体积为
224
.答案:224
9.如图是一个正方体的表面展开图,若将它折叠成正方体,相对的两个面上的数字互为相反数,则xy=
8
.答案:8
解析:
解:根据正方体表面展开图相对面的特点,可得:
3与-3是相对面(已满足互为相反数)
$ y + 2 $ 与 $ 2y - 8 $ 是相对面,所以 $ y + 2 + 2y - 8 = 0 $,解得 $ y = 2 $
$ \frac{1}{2}x + 1 $ 与 $ 2x - 11 $ 是相对面,所以 $ \frac{1}{2}x + 1 + 2x - 11 = 0 $,解得 $ x = 4 $
则 $ xy = 4×2 = 8 $
8
3与-3是相对面(已满足互为相反数)
$ y + 2 $ 与 $ 2y - 8 $ 是相对面,所以 $ y + 2 + 2y - 8 = 0 $,解得 $ y = 2 $
$ \frac{1}{2}x + 1 $ 与 $ 2x - 11 $ 是相对面,所以 $ \frac{1}{2}x + 1 + 2x - 11 = 0 $,解得 $ x = 4 $
则 $ xy = 4×2 = 8 $
8
10.如果圆柱的侧面展开图是相邻两边长分别为6,16π的长方形,那么这个圆柱的体积是
144 或 $ 384\pi $
.答案:144 或 $ 384\pi $
解析:
解:情况一:当圆柱底面周长为6,高为16π时,
底面半径$r = \frac{6}{2\pi} = \frac{3}{\pi}$,
体积$V = \pi r^2 h = \pi (\frac{3}{\pi})^2 × 16\pi = \pi × \frac{9}{\pi^2} × 16\pi = 144$。
情况二:当圆柱底面周长为16π,高为6时,
底面半径$r = \frac{16\pi}{2\pi} = 8$,
体积$V = \pi r^2 h = \pi × 8^2 × 6 = 384\pi$。
答案:144 或 $384\pi$
底面半径$r = \frac{6}{2\pi} = \frac{3}{\pi}$,
体积$V = \pi r^2 h = \pi (\frac{3}{\pi})^2 × 16\pi = \pi × \frac{9}{\pi^2} × 16\pi = 144$。
情况二:当圆柱底面周长为16π,高为6时,
底面半径$r = \frac{16\pi}{2\pi} = 8$,
体积$V = \pi r^2 h = \pi × 8^2 × 6 = 384\pi$。
答案:144 或 $384\pi$
11.在如图所示的正方体的表面展开图中,确定正方体上的点M,N的位置.


答案:
解:如答图所示.

解:如答图所示.

12.如图①是一个无盖的正方体盒子,请把下列不完整的展开图补充完整.(请画出三种)


答案:
解:如答图.(答案不唯一)


解:如答图.(答案不唯一)


13.如图,有一张长方形的硬纸,正好可以分成15个小正方形,试把它剪成3份,每份有5个小正方形相连,折起来都可以成为一个没有盖的正方体纸盒,应该怎么剪?


答案:
解:如答图.(答案不唯一)

解:如答图.(答案不唯一)
