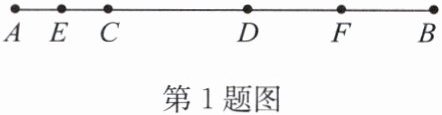
1. 如图,线段 $ AB $ 上有两点 $ C,D $,且 $ AC:CD:DB = 2:3:4 $, $ E,F $ 分别为 $ AC,DB $ 的中点, $ EF = 48 \text{ cm} $. 求 $ AB $ 的长.
答案：解: 因为 $ AC:CD:DB = 2:3:4 $，
所以设 $ AC = 2a \, \text{cm} $，$ CD = 3a \, \text{cm} $，$ DB = 4a \, \text{cm} $。
因为 $ E $，$ F $ 分别是 $ AC $，$ DB $ 的中点，
所以 $ CE = \frac{1}{2}AC = a \, \text{cm} $，$ DF = \frac{1}{2}BD = 2a \, \text{cm} $，
所以 $ EF = a + 3a + 2a = 6a = 48 $，
解得 $ a = 8 $，
所以 $ AB = AC + CD + DB = 2a + 3a + 4a = 9a = 9 × 8 = 72(\text{cm}) $。
所以设 $ AC = 2a \, \text{cm} $，$ CD = 3a \, \text{cm} $，$ DB = 4a \, \text{cm} $。
因为 $ E $，$ F $ 分别是 $ AC $，$ DB $ 的中点，
所以 $ CE = \frac{1}{2}AC = a \, \text{cm} $，$ DF = \frac{1}{2}BD = 2a \, \text{cm} $，
所以 $ EF = a + 3a + 2a = 6a = 48 $，
解得 $ a = 8 $，
所以 $ AB = AC + CD + DB = 2a + 3a + 4a = 9a = 9 × 8 = 72(\text{cm}) $。
2. 如图, $ A,O,B $ 三点在一条直线上, $ \angle AOC = 3\angle COD $, $ OE $ 平分 $ \angle BOD $, $ \angle COE = 80^{\circ} $, 求 $ \angle COD $ 的度数.
答案：解: 设 $ \angle COD = x^{\circ} $，
因为 $ \angle AOC = 3\angle COD $，所以 $ \angle AOC = 3x^{\circ} $，$ \angle AOD = 4x^{\circ} $。
因为 $ OE $ 平分 $ \angle BOD $，所以 $ \angle BOE = \angle DOE = \frac{1}{2}\angle BOD = \frac{1}{2}(180^{\circ} - \angle AOD) = 90^{\circ} - 2x^{\circ} $。
由 $ \angle COE = \angle COD + \angle DOE $，得 $ x^{\circ} + 90^{\circ} - 2x^{\circ} = 80^{\circ} $，
解得 $ x = 10 $，即 $ \angle COD = 10^{\circ} $。
因为 $ \angle AOC = 3\angle COD $，所以 $ \angle AOC = 3x^{\circ} $，$ \angle AOD = 4x^{\circ} $。
因为 $ OE $ 平分 $ \angle BOD $，所以 $ \angle BOE = \angle DOE = \frac{1}{2}\angle BOD = \frac{1}{2}(180^{\circ} - \angle AOD) = 90^{\circ} - 2x^{\circ} $。
由 $ \angle COE = \angle COD + \angle DOE $，得 $ x^{\circ} + 90^{\circ} - 2x^{\circ} = 80^{\circ} $，
解得 $ x = 10 $，即 $ \angle COD = 10^{\circ} $。
3. 如图,线段 $ AB = 12 \text{ cm} $, $ C $ 为线段 $ AB $ 上的一个动点, $ D,E $ 分别是 $ AC $ 和 $ BC $ 的中点.
(1) 若 $ C $ 恰好是 $ AB $ 的中点,则 $ DE = $
(2) 若 $ AC = 4 \text{ cm} $, 求 $ DE $ 的长;
(3) 试说明: 无论 $ AC $ 取何值(不超过 $ 12 \text{ cm} $), $ DE $ 的长不变.
(1) 若 $ C $ 恰好是 $ AB $ 的中点,则 $ DE = $
6
$ \text{cm} $;(2) 若 $ AC = 4 \text{ cm} $, 求 $ DE $ 的长;
解: 因为 $ AC = 4 \, \text{cm} $，$ D $ 是 $ AC $ 的中点，
所以 $ CD = \frac{1}{2}AC = 2 \, \text{cm} $。
因为 $ AB = 12 \, \text{cm} $，$ AC = 4 \, \text{cm} $，
所以 $ BC = AB - AC = 12 - 4 = 8(\text{cm}) $。
因为 $ E $ 是 $ BC $ 的中点，
所以 $ CE = \frac{1}{2}BC = 4 \, \text{cm} $，
所以 $ DE = DC + CE = 2 + 4 = 6(\text{cm}) $。
所以 $ CD = \frac{1}{2}AC = 2 \, \text{cm} $。
因为 $ AB = 12 \, \text{cm} $，$ AC = 4 \, \text{cm} $，
所以 $ BC = AB - AC = 12 - 4 = 8(\text{cm}) $。
因为 $ E $ 是 $ BC $ 的中点，
所以 $ CE = \frac{1}{2}BC = 4 \, \text{cm} $，
所以 $ DE = DC + CE = 2 + 4 = 6(\text{cm}) $。
(3) 试说明: 无论 $ AC $ 取何值(不超过 $ 12 \text{ cm} $), $ DE $ 的长不变.
解: 因为 $ D $，$ E $ 分别是 $ AC $ 和 $ BC $ 的中点，
所以 $ DC = \frac{1}{2}AC $，$ CE = \frac{1}{2}CB $，
所以 $ DC + CE = \frac{1}{2}(AC + CB) $，
即 $ DE = \frac{1}{2}AB = \frac{1}{2} × 12 = 6(\text{cm}) $，
故无论 $ AC $ 取何值(不超过 $ 12 \, \text{cm} $)，$ DE $ 的长不变。
所以 $ DC = \frac{1}{2}AC $，$ CE = \frac{1}{2}CB $，
所以 $ DC + CE = \frac{1}{2}(AC + CB) $，
即 $ DE = \frac{1}{2}AB = \frac{1}{2} × 12 = 6(\text{cm}) $，
故无论 $ AC $ 取何值(不超过 $ 12 \, \text{cm} $)，$ DE $ 的长不变。
答案：(1) 6
(2) 解: 因为 $ AC = 4 \, \text{cm} $，$ D $ 是 $ AC $ 的中点，
所以 $ CD = \frac{1}{2}AC = 2 \, \text{cm} $。
因为 $ AB = 12 \, \text{cm} $，$ AC = 4 \, \text{cm} $，
所以 $ BC = AB - AC = 12 - 4 = 8(\text{cm}) $。
因为 $ E $ 是 $ BC $ 的中点，
所以 $ CE = \frac{1}{2}BC = 4 \, \text{cm} $，
所以 $ DE = DC + CE = 2 + 4 = 6(\text{cm}) $。
(3) 解: 因为 $ D $，$ E $ 分别是 $ AC $ 和 $ BC $ 的中点，
所以 $ DC = \frac{1}{2}AC $，$ CE = \frac{1}{2}CB $，
所以 $ DC + CE = \frac{1}{2}(AC + CB) $，
即 $ DE = \frac{1}{2}AB = \frac{1}{2} × 12 = 6(\text{cm}) $，
故无论 $ AC $ 取何值(不超过 $ 12 \, \text{cm} $)，$ DE $ 的长不变。
(2) 解: 因为 $ AC = 4 \, \text{cm} $，$ D $ 是 $ AC $ 的中点，
所以 $ CD = \frac{1}{2}AC = 2 \, \text{cm} $。
因为 $ AB = 12 \, \text{cm} $，$ AC = 4 \, \text{cm} $，
所以 $ BC = AB - AC = 12 - 4 = 8(\text{cm}) $。
因为 $ E $ 是 $ BC $ 的中点，
所以 $ CE = \frac{1}{2}BC = 4 \, \text{cm} $，
所以 $ DE = DC + CE = 2 + 4 = 6(\text{cm}) $。
(3) 解: 因为 $ D $，$ E $ 分别是 $ AC $ 和 $ BC $ 的中点，
所以 $ DC = \frac{1}{2}AC $，$ CE = \frac{1}{2}CB $，
所以 $ DC + CE = \frac{1}{2}(AC + CB) $，
即 $ DE = \frac{1}{2}AB = \frac{1}{2} × 12 = 6(\text{cm}) $，
故无论 $ AC $ 取何值(不超过 $ 12 \, \text{cm} $)，$ DE $ 的长不变。
4. 如图, $ O $ 是直线 $ AB $ 上的一点, $ \angle COD $ 是直角, $ OE $ 平分 $ \angle BOC $.
(1) 如图①, 若 $ \angle AOC = 30^{\circ} $, 则 $ \angle DOE = $______
(1) 如图①, 若 $ \angle AOC = 30^{\circ} $, 则 $ \angle DOE = $______
15°
;答案：(1) $ 15^{\circ} $
(2) 解: $ \angle AOC = 2\angle DOE $。
理由: 因为 $ \angle COD $ 是直角，$ OE $ 平分 $ \angle BOC $，
所以 $ \angle COE = \angle BOE = 90^{\circ} - \angle DOE $，
所以 $ \angle AOC = 180^{\circ} - \angle BOC = 180^{\circ} - 2\angle COE = 180^{\circ} - 2(90^{\circ} - \angle DOE) = 2\angle DOE $。
(3) 解: $ \angle AOC = 360^{\circ} - 2\angle DOE $。
理由: 因为 $ OE $ 平分 $ \angle BOC $，
所以 $ \angle BOC = 2\angle COE $，
则 $ \angle AOC = 180^{\circ} - \angle BOC = 180^{\circ} - 2\angle COE = 180^{\circ} - 2(\angle DOE - 90^{\circ}) = 360^{\circ} - 2\angle DOE $。
(2) 解: $ \angle AOC = 2\angle DOE $。
理由: 因为 $ \angle COD $ 是直角，$ OE $ 平分 $ \angle BOC $，
所以 $ \angle COE = \angle BOE = 90^{\circ} - \angle DOE $，
所以 $ \angle AOC = 180^{\circ} - \angle BOC = 180^{\circ} - 2\angle COE = 180^{\circ} - 2(90^{\circ} - \angle DOE) = 2\angle DOE $。
(3) 解: $ \angle AOC = 360^{\circ} - 2\angle DOE $。
理由: 因为 $ OE $ 平分 $ \angle BOC $，
所以 $ \angle BOC = 2\angle COE $，
则 $ \angle AOC = 180^{\circ} - \angle BOC = 180^{\circ} - 2\angle COE = 180^{\circ} - 2(\angle DOE - 90^{\circ}) = 360^{\circ} - 2\angle DOE $。