8. 如图,OC 是$∠AOB$的平分线,$∠DOC= 3∠BOD,∠BOD= 18^{\circ }$,则$∠AOD$的度数为
90°
.答案:90°
解析:
解:因为∠DOC=3∠BOD,∠BOD=18°,所以∠DOC=3×18°=54°。
所以∠BOC=∠DOC - ∠BOD=54° - 18°=36°。
因为OC是∠AOB的平分线,所以∠AOC=∠BOC=36°。
所以∠AOD=∠AOC + ∠COB + ∠BOD=36° + 36° + 18°=90°。
90°
所以∠BOC=∠DOC - ∠BOD=54° - 18°=36°。
因为OC是∠AOB的平分线,所以∠AOC=∠BOC=36°。
所以∠AOD=∠AOC + ∠COB + ∠BOD=36° + 36° + 18°=90°。
90°
9. 如图,OA 的方向是北偏东$20^{\circ }$,OC 的方向是北偏西$40^{\circ }$,若$∠AOC= ∠AOB$,则 OB 的方向是
北偏东 80°
.答案:北偏东 80°
解析:
解:
∵OA的方向是北偏东20°,OC的方向是北偏西40°,
∴∠AOC = 20° + 40° = 60°。
∵∠AOC = ∠AOB,
∴∠AOB = 60°。
∵OA是北偏东20°,
∴OB的方向是北偏东20° + 60° = 80°。
北偏东80°
∵OA的方向是北偏东20°,OC的方向是北偏西40°,
∴∠AOC = 20° + 40° = 60°。
∵∠AOC = ∠AOB,
∴∠AOB = 60°。
∵OA是北偏东20°,
∴OB的方向是北偏东20° + 60° = 80°。
北偏东80°
10. 如图,已知$∠1,∠2$. 求作$∠AOB$,使$∠AOB= ∠1+∠2$.(用尺规作图,不要求写作法,但要保留作图痕迹)
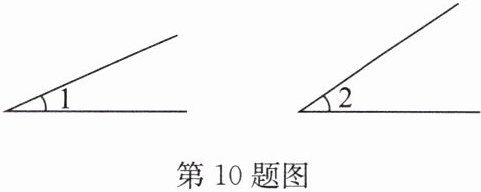

答案:
解: 如答图,∠AOB 即为所求。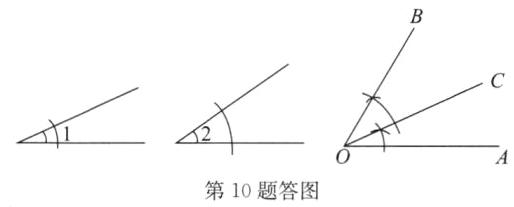
解: 如答图,∠AOB 即为所求。

11. 如图,O 为直线 AB 上一点,$∠AOC= 50^{\circ },OD平分∠AOC,∠DOE= 90^{\circ }$.
(1)请写出图中小于平角的角;
(2)求$∠BOD$的度数;
(3)请通过计算说明 OE 是否平分$∠BOC$.

(1)请写出图中小于平角的角;
(2)求$∠BOD$的度数;
(3)请通过计算说明 OE 是否平分$∠BOC$.

答案:解: (1) 图中小于平角的角有∠AOD,∠AOC,∠AOE,∠DOC,∠DOE,∠DOB,∠COE,∠COB,∠EOB,共 9 个。(2) 因为∠AOC = 50°,OD 平分∠AOC,所以∠AOD = $\frac{1}{2}$∠AOC = 25°,所以∠BOD = 180° - ∠AOD = 180° - 25° = 155°。(3) 因为∠DOE = 90°,∠DOC = $\frac{1}{2}$∠AOC = 25°,所以∠COE = ∠DOE - ∠DOC = 90° - 25° = 65°。又因为∠BOE = ∠BOD - ∠DOE = 155° - 90° = 65°,所以∠COE = ∠BOE,即 OE 平分∠BOC。
12. (1)如图,$∠AOB= 90^{\circ },∠BOC= 30^{\circ }$,OM 平分$∠AOC$,ON 平分$∠BOC$,求$∠MON$的度数;
(2)如果(1)中$∠AOB= α$,其他条件不变,求$∠MON$的度数;
(3)如果(1)中$∠BOC= β$(β为锐角),其他条件不变,求$∠MON$的度数;
(4)从(1)(2)(3)的结果中能看出什么规律?

(2)如果(1)中$∠AOB= α$,其他条件不变,求$∠MON$的度数;
(3)如果(1)中$∠BOC= β$(β为锐角),其他条件不变,求$∠MON$的度数;
(4)从(1)(2)(3)的结果中能看出什么规律?

答案:解: (1) 因为 OM 平分∠AOC,ON 平分∠BOC,所以∠MOC = $\frac{1}{2}$∠AOC,∠NOC = $\frac{1}{2}$∠BOC,所以∠MON = ∠MOC - ∠NOC = $\frac{1}{2}$∠AOC - $\frac{1}{2}$∠BOC = $\frac{1}{2}$(∠AOC - ∠BOC) = $\frac{1}{2}$∠AOB = $\frac{1}{2}$×90° = 45°。(2) ∠MON = $\frac{1}{2}$∠AOB = $\frac{\alpha}{2}$。(3) ∠MON = $\frac{1}{2}$∠AOB = 45°。(4) 从 (1)(2)(3) 的结果中可以看出∠MON 的度数总等于∠AOB 度数的一半,而与锐角∠BOC 的度数无关。