1. 有下列说法:①射线AB与射线BA是同一条射线;②线段AB是直线AB的一部分;③延长线段AB到点C,使AB= AC;④射线AB与射线BA的公共部分是线段AB.其中正确的个数是(
A.1
B.2
C.3
D.4
B
)A.1
B.2
C.3
D.4
答案:B
解析:
解:①射线AB端点为A,方向从A到B;射线BA端点为B,方向从B到A,不是同一条射线,错误。
②线段AB是直线AB上两点A、B之间的部分,正确。
③延长线段AB到点C,则AC=AB+BC,AC>AB,错误。
④射线AB与射线BA的公共部分是线段AB,正确。
正确的有②④,共2个。
答案:B
②线段AB是直线AB上两点A、B之间的部分,正确。
③延长线段AB到点C,则AC=AB+BC,AC>AB,错误。
④射线AB与射线BA的公共部分是线段AB,正确。
正确的有②④,共2个。
答案:B
2. 如图,下列说法错误的是(
A.∠DAO也可用∠DAC表示
B.∠COB也可用∠O表示
C.∠2也可用∠OBC表示
D.∠CDB也可用∠1表示
B
)A.∠DAO也可用∠DAC表示
B.∠COB也可用∠O表示
C.∠2也可用∠OBC表示
D.∠CDB也可用∠1表示
答案:B
解析:
A. ∠DAO与∠DAC顶点相同,两边相同,可表示,正确;
B. 以O为顶点的角有∠AOD、∠DOC、∠COB、∠BOA等,不能用∠O表示∠COB,错误;
C. ∠2与∠OBC顶点相同,两边相同,可表示,正确;
D. ∠CDB与∠1顶点相同,两边相同,可表示,正确。
答案:B
B. 以O为顶点的角有∠AOD、∠DOC、∠COB、∠BOA等,不能用∠O表示∠COB,错误;
C. ∠2与∠OBC顶点相同,两边相同,可表示,正确;
D. ∠CDB与∠1顶点相同,两边相同,可表示,正确。
答案:B
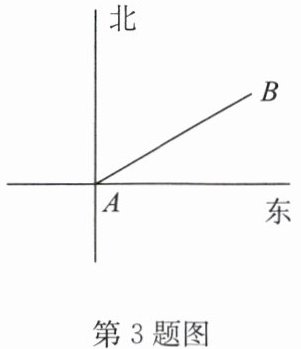
3. (2024·崇川区月考)如图,轮船航行到A处时,观测到小岛B的方向是北偏东60°,那么同时从小岛B观测轮船的方向是(
A.北偏东60°
B.北偏东30°
C.南偏东30°
D.南偏西60°
D
) 
A.北偏东60°
B.北偏东30°
C.南偏东30°
D.南偏西60°
答案:D
解析:
解:轮船在A处观测小岛B的方向是北偏东60°,即∠NAB=60°(N为A处正北方向)。
因为方向是相对的,且正北与正南方向平行,由平行线性质可知,从小岛B观测轮船A的方向与北偏东60°互为相反方向,即南偏西60°。
答案:D
因为方向是相对的,且正北与正南方向平行,由平行线性质可知,从小岛B观测轮船A的方向与北偏东60°互为相反方向,即南偏西60°。
答案:D
4. 如图,D是线段AB上一点,C是线段BD的中点,若AB= 8cm,CD= 3cm,则线段AD的长为(
A.5cm
B.4cm
C.3cm
D.2cm
D
)A.5cm
B.4cm
C.3cm
D.2cm
答案:D
解析:
解:∵C是线段BD的中点,CD=3cm
∴BD=2CD=2×3=6cm
∵AB=8cm
∴AD=AB-BD=8-6=2cm
答案:D
∴BD=2CD=2×3=6cm
∵AB=8cm
∴AD=AB-BD=8-6=2cm
答案:D
5. 如图,图中共有线段
3
条,射线12
条.答案:3 12
解析:
线段:图中线段有DE、EB、DB,共3条。
射线:以D为端点的射线有4条,以B为端点的射线有4条,以E为端点的射线有4条,共12条。
答案:3 12
射线:以D为端点的射线有4条,以B为端点的射线有4条,以E为端点的射线有4条,共12条。
答案:3 12
6. 124.24°=
124°14′24″
.(化成度、分、秒的形式)答案:$124 ^ { \circ } 14 ^ { \prime } 24 ^ { \prime \prime }$
解析:
解:$0.24^{\circ} = 0.24 × 60' = 14.4'$
$0.4' = 0.4 × 60'' = 24''$
$124.24^{\circ} = 124^{\circ}14'24''$
$124^{\circ}14'24''$
$0.4' = 0.4 × 60'' = 24''$
$124.24^{\circ} = 124^{\circ}14'24''$
$124^{\circ}14'24''$
7. 下列生产和生活现象:①用两个钉子就可以把木条固定在墙上;②把弯曲的公路改直,就能缩短路程;③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;④从A地到B地架设电线,总是尽可能沿着线段AB架设.其中能用“两点之间,线段最短”来解释的有
②④
.(填序号)答案:②④
8. 上午6点45分时,时针与分针所夹锐角的度数为
$67.5 ^ { \circ }$
.答案:$67.5 ^ { \circ }$
解析:
解:分针每分钟转$6^\circ$,$45$分钟转$45×6^\circ=270^\circ$。
时针每小时转$30^\circ$,每分钟转$0.5^\circ$,6小时45分钟转$6×30^\circ + 45×0.5^\circ=180^\circ +22.5^\circ=202.5^\circ$。
夹角为$|270^\circ - 202.5^\circ|=67.5^\circ$。
$67.5^\circ$
时针每小时转$30^\circ$,每分钟转$0.5^\circ$,6小时45分钟转$6×30^\circ + 45×0.5^\circ=180^\circ +22.5^\circ=202.5^\circ$。
夹角为$|270^\circ - 202.5^\circ|=67.5^\circ$。
$67.5^\circ$
9. 已知∠AOB= 90°,射线OC在∠AOB内部,且∠AOC= 20°,∠COD= 50°,射线OE,OF分别平分∠BOC,∠COD,则∠EOF的度数是
$10 ^ { \circ }$或$60 ^ { \circ }$
.答案:$10 ^ { \circ }$或$60 ^ { \circ }$
解析:
解:
∵∠AOB=90°,∠AOC=20°
∴∠BOC=∠AOB - ∠AOC=70°
∵OE平分∠BOC
∴∠COE=∠BOC/2=35°
情况1:OD在∠AOC内部
∵∠AOC=20°,∠COD=50°,50°>20°,此情况不成立。
情况2:OD在∠BOC内部
∵∠COD=50°,OF平分∠COD
∴∠COF=∠COD/2=25°
∴∠EOF=∠COE - ∠COF=35° - 25°=10°
情况3:OD在∠AOB外部(靠近OB一侧)
∵∠COD=50°,OF平分∠COD
∴∠COF=∠COD/2=25°
∴∠EOF=∠COE + ∠COF=35° + 25°=60°
综上,∠EOF的度数是10°或60°。
∵∠AOB=90°,∠AOC=20°
∴∠BOC=∠AOB - ∠AOC=70°
∵OE平分∠BOC
∴∠COE=∠BOC/2=35°
情况1:OD在∠AOC内部
∵∠AOC=20°,∠COD=50°,50°>20°,此情况不成立。
情况2:OD在∠BOC内部
∵∠COD=50°,OF平分∠COD
∴∠COF=∠COD/2=25°
∴∠EOF=∠COE - ∠COF=35° - 25°=10°
情况3:OD在∠AOB外部(靠近OB一侧)
∵∠COD=50°,OF平分∠COD
∴∠COF=∠COD/2=25°
∴∠EOF=∠COE + ∠COF=35° + 25°=60°
综上,∠EOF的度数是10°或60°。