10. 如图,平面上有四个点A,B,C,D.
(1)根据下列语句画图:
①画射线AB;
②画直线CD交射线AB于点E;
③在线段BC的延长线上取一点F,使CF= CD,连接AD,AF.
(2)图中以A为顶点的角中,小于平角的角有哪几个?

(1)根据下列语句画图:
①画射线AB;
②画直线CD交射线AB于点E;
③在线段BC的延长线上取一点F,使CF= CD,连接AD,AF.
(2)图中以A为顶点的角中,小于平角的角有哪几个?

答案:
解:(1)如答图
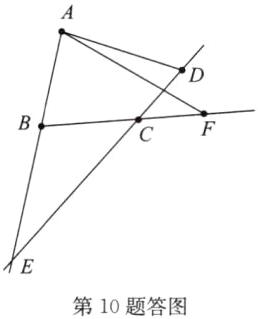
(2)如答图,以A为顶点的角中,小于平角的角有$\angle DAB$,$\angle DAF$,$\angle BAF$,共3个.
解:(1)如答图

(2)如答图,以A为顶点的角中,小于平角的角有$\angle DAB$,$\angle DAF$,$\angle BAF$,共3个.
11. 已知C是线段AB上一点,D是线段AB的中点,若AB= 10cm,BC= 3cm.
(1)求线段CD的长;
(2)若E是直线AB上一点,且BE= 2cm,F是BE的中点,求线段DF的长.
(1)求线段CD的长;
(2)若E是直线AB上一点,且BE= 2cm,F是BE的中点,求线段DF的长.
答案:
解:(1)因为D是线段AB的中点,$AB = 10 \mathrm {cm}$,
所以$BD = \frac { 1 } { 2 }AB = 5 \mathrm {cm}$.
因为$BC = 3 \mathrm {cm}$,
所以$CD = BD - BC = 2 \mathrm {cm}$.
(2)当点E在AB的延长线上时,如答图①,

因为$BE = 2 \mathrm {cm}$,F是BE的中点,
所以$BF = \frac { 1 } { 2 }BE = 1 \mathrm {cm}$,
所以$DF = BD + BF = 5 + 1 = 6 ( \mathrm {cm} )$;
当点E在线段AB上时,如答图②,

因为$BE = 2 \mathrm {cm}$,F是BE的中点,
所以$BF = \frac { 1 } { 2 }BE = 1 \mathrm {cm}$,
所以$DF = BD - BF = 5 - 1 = 4 ( \mathrm {cm} )$.
综上所述,线段DF的长为$6 \mathrm {cm}$或$4 \mathrm {cm}$.
解:(1)因为D是线段AB的中点,$AB = 10 \mathrm {cm}$,
所以$BD = \frac { 1 } { 2 }AB = 5 \mathrm {cm}$.
因为$BC = 3 \mathrm {cm}$,
所以$CD = BD - BC = 2 \mathrm {cm}$.
(2)当点E在AB的延长线上时,如答图①,

因为$BE = 2 \mathrm {cm}$,F是BE的中点,
所以$BF = \frac { 1 } { 2 }BE = 1 \mathrm {cm}$,
所以$DF = BD + BF = 5 + 1 = 6 ( \mathrm {cm} )$;
当点E在线段AB上时,如答图②,

因为$BE = 2 \mathrm {cm}$,F是BE的中点,
所以$BF = \frac { 1 } { 2 }BE = 1 \mathrm {cm}$,
所以$DF = BD - BF = 5 - 1 = 4 ( \mathrm {cm} )$.
综上所述,线段DF的长为$6 \mathrm {cm}$或$4 \mathrm {cm}$.
12. 已知O为直线AB上一点,射线OD,OC,OE位于直线AB上方,OD在OE的左侧,∠AOC= 120°,∠DOE= 80°.
(1)如图①,当OD平分∠AOC时,求∠EOB的度数;
(2)点F在射线OB上,若射线OF绕点O逆时针旋转n°(0<n<180且n≠60),∠FOA= 3∠AOD.当∠DOE在∠AOC内部(如图②)和∠DOE的两边在射线OC的两侧(如图③)时,求∠EOF和∠EOC的数量关系.

(1)如图①,当OD平分∠AOC时,求∠EOB的度数;
(2)点F在射线OB上,若射线OF绕点O逆时针旋转n°(0<n<180且n≠60),∠FOA= 3∠AOD.当∠DOE在∠AOC内部(如图②)和∠DOE的两边在射线OC的两侧(如图③)时,求∠EOF和∠EOC的数量关系.

答案:解:(1)因为OD平分$\angle AOC$,
所以$\angle AOD = \angle COD = \frac { 1 } { 2 }\angle AOC = 60 ^ { \circ }$.
因为$\angle DOE = 80 ^ { \circ }$,
所以$\angle AOE = \angle AOD + \angle DOE = 60 ^ { \circ } + 80 ^ { \circ } = 140 ^ { \circ }$,
所以$\angle EOB = 180 ^ { \circ } - \angle AOE = 40 ^ { \circ }$.
(2)当$\angle DOE$在$\angle AOC$内部时,
令$\angle AOD = x ^ { \circ }$,则$\angle DOF = 2 x ^ { \circ }$,$\angle EOF = 80 ^ { \circ } - 2 x ^ { \circ }$,
所以$\angle EOC = 120 ^ { \circ } - ( x ^ { \circ } + 2 x ^ { \circ } + 80 ^ { \circ } - 2 x ^ { \circ } ) = 40 ^ { \circ } - x ^ { \circ }$,所以$\angle EOF = 2\angle EOC$.
当$\angle DOE$的两边在射线OC的两侧时,令$\angle AOD = x ^ { \circ }$,则$\angle DOF = 2 x ^ { \circ }$,$\angle DOC = 120 ^ { \circ } - x ^ { \circ }$,$\angle EOF = 2 x ^ { \circ } - 80 ^ { \circ }$,所以$\angle EOC = 80 ^ { \circ } - ( 120 ^ { \circ } - x ^ { \circ } ) = x ^ { \circ } - 40 ^ { \circ }$,
所以$\angle EOF = 2\angle EOC$;
综上,$\angle EOF$和$\angle EOC$的数量关系为$\angle EOF = 2\angle EOC$.
所以$\angle AOD = \angle COD = \frac { 1 } { 2 }\angle AOC = 60 ^ { \circ }$.
因为$\angle DOE = 80 ^ { \circ }$,
所以$\angle AOE = \angle AOD + \angle DOE = 60 ^ { \circ } + 80 ^ { \circ } = 140 ^ { \circ }$,
所以$\angle EOB = 180 ^ { \circ } - \angle AOE = 40 ^ { \circ }$.
(2)当$\angle DOE$在$\angle AOC$内部时,
令$\angle AOD = x ^ { \circ }$,则$\angle DOF = 2 x ^ { \circ }$,$\angle EOF = 80 ^ { \circ } - 2 x ^ { \circ }$,
所以$\angle EOC = 120 ^ { \circ } - ( x ^ { \circ } + 2 x ^ { \circ } + 80 ^ { \circ } - 2 x ^ { \circ } ) = 40 ^ { \circ } - x ^ { \circ }$,所以$\angle EOF = 2\angle EOC$.
当$\angle DOE$的两边在射线OC的两侧时,令$\angle AOD = x ^ { \circ }$,则$\angle DOF = 2 x ^ { \circ }$,$\angle DOC = 120 ^ { \circ } - x ^ { \circ }$,$\angle EOF = 2 x ^ { \circ } - 80 ^ { \circ }$,所以$\angle EOC = 80 ^ { \circ } - ( 120 ^ { \circ } - x ^ { \circ } ) = x ^ { \circ } - 40 ^ { \circ }$,
所以$\angle EOF = 2\angle EOC$;
综上,$\angle EOF$和$\angle EOC$的数量关系为$\angle EOF = 2\angle EOC$.